Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tang, Chi-Wu
and
Tang, Min
2010.
Note on a Result of Haddad and Helou.
Integers,
Vol. 10,
Issue. 2,
TANG, MIN
2010.
A NOTE ON A RESULT OF RUZSA, II.
Bulletin of the Australian Mathematical Society,
Vol. 82,
Issue. 2,
p.
340.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
275.
Yu, Wang-Xing
and
Zhao, Jun-Jia
2026.
An optimal lower bound for the size of the restricted sumsets containing powers.
Journal of Number Theory,
Vol. 280,
Issue. ,
p.
785.

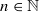 and
and 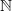 . Erdös and Turán conjectured that, for any basis
. Erdös and Turán conjectured that, for any basis 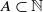 for which
for which 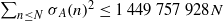 for large enough
for large enough 