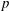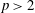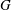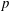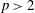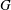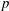Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Orfi, R.
and
Fouladi, S.
2018.
Noninner Automorphisms of Order p in Some Finite p-Groups.
Bulletin of the Iranian Mathematical Society,
Vol. 44,
Issue. 5,
p.
1295.
Garg, Rohit
and
Singh, Mandeep
2021.
Finite p-groups with non-cyclic center have a non-inner automorphism of order p.
Archiv der Mathematik,
Vol. 117,
Issue. 2,
p.
129.
Fouladi, S.
and
Orfi, R.
2021.
A note on the existence of noninner automorphisms of order p in some finite p-groups.
Journal of Algebra and Its Applications,
Vol. 20,
Issue. 04,
p.
2150067.
Zhang, Qinhai
2022.
Some unsolvable conjectures in finite p-groups.
Frontiers of Mathematics in China,
Vol. 17,
Issue. 1,
p.
1.
Singh, Mandeep
and
Sharma, Mahak
2025.
Finite p-groups with cyclic center have non-inner automorphisms of order p.
Archiv der Mathematik,
Vol. 124,
Issue. 5,
p.
469.