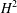Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Choulli, Mourad
2021.
The unique continuation property for second order evolution PDEs.
Partial Differential Equations and Applications,
Vol. 2,
Issue. 5,
Choulli, Mourad
and
Yamamoto, Masahiro
2021.
Global stability result for parabolic Cauchy problems.
Journal of Inverse and Ill-posed Problems,
Vol. 29,
Issue. 6,
p.
895.
Bellassoued, Mourad
and
Choulli, Mourad
2023.
Global logarithmic stability of a Cauchy problem for anisotropic wave equations.
Partial Differential Equations and Applications,
Vol. 4,
Issue. 3,
Choulli, Mourad
2024.
Uniqueness of continuation for semilinear elliptic equations.
Partial Differential Equations and Applications,
Vol. 5,
Issue. 4,
Choulli, Mourad
and
Takase, Hiroshi
2025.
Lipschitz stability for an elliptic inverse problem with two measurements.
Research in the Mathematical Sciences,
Vol. 12,
Issue. 2,
Choulli, Mourad
2026.
Two parabolic inverse problems for an equation with unbounded zero-order coefficient.
Inverse Problems and Imaging,
Vol. 20,
Issue. 0,
p.
236.