Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hamilton, E.P
and
Nashed, M.Z
1982.
Global and local variational derivatives and integral representations of Gâteaux differentials.
Journal of Functional Analysis,
Vol. 49,
Issue. 1,
p.
128.
Hamilton, E. P.
Nashed, M. Z.
and
Brosowski, B.
1983.
Variational derivatives and p‐gradients of functionals on spaces of continuously differentiable functions.
Mathematical Methods in the Applied Sciences,
Vol. 5,
Issue. 1,
p.
530.
Nashed, M.Z.
and
Hamilton, E.P.
1991.
Local and global bivariational gradients and singular variational derivatives of functionals on Cn[a,b].
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 17,
Issue. 9,
p.
841.
Athanassoulis, Gerassimos A
and
Mamis, Konstantinos I
2019.
Extensions of the Novikov–Furutsu theorem, obtained by using Volterra functional calculus.
Physica Scripta,
Vol. 94,
Issue. 11,
p.
115217.

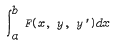 fails to possess a variational derivative, contrary to what is claimed by Gelfand and Fomin. A modified definition is given with respect to which the functional does possess a variational derivative.
fails to possess a variational derivative, contrary to what is claimed by Gelfand and Fomin. A modified definition is given with respect to which the functional does possess a variational derivative.