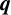Hostname: page-component-5cf477f64f-fcbfl Total loading time: 0 Render date: 2025-04-04T08:31:23.485Z Has data issue: false hasContentIssue false
  • English
  • Français

A NEW $\boldsymbol {q}$-ANALOGUE OF VAN HAMME’S (A.2) SUPERCONGRUENCE

Part of: Sequences and sets Basic hypergeometric functions Elementary number theory

Published online by Cambridge University Press:  20 May 2022

VICTOR J. W. GUO Open the ORCID record for VICTOR J. W. GUO [Opens in a new window]
VICTOR J. W. GUO*
Affiliation:
School of Mathematics and Statistics, Huaiyin Normal University, Huai’an 223300, Jiangsu, PR China
*
e-mail: jwguo@math.ecnu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We give a new q-analogue of the (A.2) supercongruence of Van Hamme. Our proof employs Andrews’ multiseries generalisation of Watso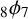n’s $_{8}\phi _{7}$ transformation, Andrews’ terminating q-analogue of Watson’s 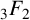$_{3}F_{2}$ summation, a q-Watson-type summation due to Wei–Gong–Li and the creative microscoping method, developed by the author and Zudilin [‘A q-microscope for supercongruences’, Adv. Math. 346 (2019), 329–358]. As a conclusion, we confirm a weaker form of Conjecture 4.5 by the author [‘Some generalizations of a supercongruence of van Hamme’, Integral Transforms Spec. Funct. 28 (2017), 888–899].

Keywords

basic hypergeometric seriesq-congruencesupercongruencecreative microscoping

MSC classification

Primary: 11B65: Binomial coefficients; factorials; $q$-identities
Secondary: 11A07: Congruences; primitive roots; residue systems 33D15: Basic hypergeometric functions in one variable, $_rphi_s$
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 1 , February 2023 , pp. 22 - 30
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, G. E., ‘Problems and prospects for basic hypergeometric functions’, in Theory and Application for Basic Hypergeometric Functions, Mathematics Research Center, the University of Wisconsin–Madison, 35 (ed. Askey, R. A.) (Academic Press, New York, 1975), 191–224.Google Scholar
Andrews, G. E., ‘On $q$ -analogues of the Watson and Whipple summations’, SIAM J. Math. Anal. 7 (1976), 332–336.CrossRefGoogle Scholar
Gasper, G. and Rahman, M., Basic Hypergeometric Series, 2nd edn, Encyclopedia of Mathematics and Its Applications, 96 (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Guo, V. J. W., ‘Some generalizations of a supercongruence of Van Hamme’, Integral Transforms Spec. Funct. 28 (2017), 888–899.CrossRefGoogle Scholar
Guo, V. J. W., ‘ A $q$ -analogue of the (A.2) supercongruence of Van Hamme for primes ${p\equiv 1 \pmod 4}$ ’, Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 114 (2020), Article no. 123.Google Scholar
Guo, V. J. W. and Schlosser, M. J., ‘Some $q$ -supercongruences from transformation formulas for basic hypergeometric series’, Constr. Approx. 53 (2021), 155–200.10.1007/s00365-020-09524-zCrossRefGoogle Scholar
Guo, V. J. W. and Zudilin, W., ‘A $q$ -microscope for supercongruences’, Adv. Math. 346 (2019), 329–358.CrossRefGoogle Scholar
Guo, V. J. W. and Zudilin, W., ‘A common $q$ -analogue of two supercongruences’, Results Math. 75 (2020), Article no. 46.CrossRefGoogle Scholar
Guo, V. J. W. and Zudilin, W., ‘A q-microscope for supercongruences’, Adv. Math. 346 (2019), 329–358.CrossRefGoogle Scholar
Liu, J.-C., ‘On Van Hamme’s (A.2) and (H.2) supercongruences’, J. Math. Anal. Appl. 471 (2019), 613–622.CrossRefGoogle Scholar
McCarthy, D. and Osburn, R., ‘A $p$ -adic analogue of a formula of Ramanujan’, Arch. Math. (Basel) 91 (2008), 492–504.CrossRefGoogle Scholar
Robert, A. M., A Course in $p$ -Adic Analysis, Graduate Texts in Mathematics, 198 (Springer-Verlag, New York, 2000).CrossRefGoogle Scholar
Swisher, H., ‘On the supercongruence conjectures of Van Hamme’, Res. Math. Sci. 2 (2015), Article no. 18.CrossRefGoogle Scholar
Van Hamme, L., ‘Proof of a conjecture of Beukers on Apéry numbers’, in Proceedings of the Conference on $p$ -Adic Analysis, Houthalen, 1987 (eds. N. De Grande-De Kimpe and L. Van Hamme) (Vrije Universiteit Brussel, Brussels, 1986), 189–195.Google Scholar
Van Hamme, L., ‘Some conjectures concerning partial sums of generalized hypergeometric series’, in $p$ -Adic Functional Analysis, Nijmegen, 1996, Lecture Notes in Pure and Applied Mathematics, 192 (eds. W. H. Schikhof, C. Perez-Garcia and J. Kakol) (Dekker, New York, 1997), 223–236.Google Scholar
Wang, X. and Yue, M., ‘ A $q$ -analogue of the (A.2) supercongruence of Van Hamme for any prime $p\equiv 3 \pmod 4$ ’, Int. J. Number Theory 16 (2020), 1325–1335.CrossRefGoogle Scholar
Wei, C., ‘Some $q$ -supercongruences modulo the fourth power of a cyclotomic polynomia’, J. Combin. Theory Ser. A 182 (2021), Article no. 105469.Google Scholar
Wei, C., ‘Some $q$ -supercongruences modulo the fifth and sixth powers of a cyclotomic polynomial’, Preprint, 2021, arXiv:2104.07025.CrossRefGoogle Scholar
Wei, C., Gong, D. and Li, J., ‘Summation formulae for $q$ -Watson type ${}_4{\phi}_3$ -series’, Discrete Math. 313 (2013), 1589–1593.CrossRefGoogle Scholar