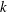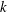Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Protasov, Vladimir Y.
and
Jungers, Raphaël M.
2015.
Resonance and marginal instability of switching systems.
Nonlinear Analysis: Hybrid Systems,
Vol. 17,
Issue. ,
p.
81.
Bell, Jason P.
Coons, Michael
and
Hare, Kevin G.
2016.
Growth degree classification for finitely generated semigroups of integer matrices.
Semigroup Forum,
Vol. 92,
Issue. 1,
p.
23.
Protasov, Vladimir Yu.
2016.
Linear switching systems with slow growth of trajectories.
Systems & Control Letters,
Vol. 90,
Issue. ,
p.
54.
Coons, Michael
2017.
Regular Sequences and the Joint Spectral Radius.
International Journal of Foundations of Computer Science,
Vol. 28,
Issue. 02,
p.
135.
Zhang, Jie-Meng
Chen, Jin
Guo, Ying-Jun
and
Wen, Zhi-Xiong
2017.
Morphisms on infinite alphabets, countable states automata and regular sequences.
Chaos, Solitons & Fractals,
Vol. 99,
Issue. ,
p.
263.
Coons, Michael
and
Spiegelhofer, Lukas
2018.
Sequences, Groups, and Number Theory.
p.
37.
Allouche, Jean-Paul
and
Goldmakher, Leo
2018.
Mock characters and the Kronecker symbol.
Journal of Number Theory,
Vol. 192,
Issue. ,
p.
356.
Zhang, Jie-Meng
Guo, Ying-Jun
and
Wen, Zhi-Xiong
2018.
On the regularity of {⌊logb(αn+β)⌋}n≥0.
Theoretical Computer Science,
Vol. 707,
Issue. ,
p.
82.
Klurman, Oleksiy
and
Kurlberg, Pär
2020.
A note on multiplicative automatic sequences, II.
Bulletin of the London Mathematical Society,
Vol. 52,
Issue. 1,
p.
185.
Konieczny, Jakub
2020.
On multiplicative automatic sequences.
Bulletin of the London Mathematical Society,
Vol. 52,
Issue. 1,
p.
175.
Konieczny, Jakub
Lemańczyk, Mariusz
and
Müllner, Clemens
2022.
Multiplicative automatic sequences.
Mathematische Zeitschrift,
Vol. 300,
Issue. 2,
p.
1297.
Morris, Ian D.
and
Varney, Jonah
2023.
A note on the marginal instability rates of two-dimensional linear cocycles.
Dynamical Systems,
Vol. 38,
Issue. 4,
p.
525.
Varney, Jonah
and
Morris, Ian D.
2025.
On marginal growth rates of matrix products.
Linear Algebra and its Applications,
Vol. 709,
Issue. ,
p.
132.