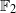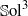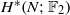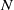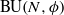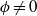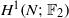Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Martins, Sérgio Tadao
2015.
Diagonal approximation and the cohomology ring of torus fiber bundles.
International Journal of Algebra and Computation,
Vol. 25,
Issue. 03,
p.
493.
Gonçalves, Daciberg Lima
and
Martins, Sérgio Tadao
2018.
The cohomology ring of the sapphires that admit the Sol geometry.
International Journal of Algebra and Computation,
Vol. 28,
Issue. 03,
p.
365.
HILLMAN, J. A.
2018.
-MANIFOLDS.
Journal of the Australian Mathematical Society,
Vol. 105,
Issue. 1,
p.
46.
Matmat, Chahrazade
and
Blanchet, Christian
2024.
Obstruction Theory for the $$\mathbb {Z}_2$$-Index of 4-Manifolds.
Bulletin of the Iranian Mathematical Society,
Vol. 50,
Issue. 5,