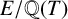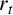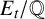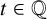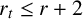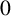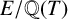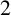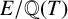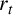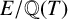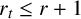1 Introduction
Let
![]() $\pi : \mathcal {E} \rightarrow \mathbb {P}^1$
be a nonconstant elliptic surface defined over
$\pi : \mathcal {E} \rightarrow \mathbb {P}^1$
be a nonconstant elliptic surface defined over
![]() $\mathbb {Q}$
. By this, we mean a two-dimensional projective variety
$\mathbb {Q}$
. By this, we mean a two-dimensional projective variety
![]() $\mathcal {E}$
endowed with a morphism
$\mathcal {E}$
endowed with a morphism
![]() $\pi $
as above such that all but finitely many fibres of
$\pi $
as above such that all but finitely many fibres of
![]() $\pi $
are curves of genus one and such that there exists a section
$\pi $
are curves of genus one and such that there exists a section
![]() $\sigma $
to
$\sigma $
to
![]() $\pi $
. Let
$\pi $
. Let
![]() $E/\mathbb {Q}(T)$
be the generic fibre of
$E/\mathbb {Q}(T)$
be the generic fibre of
![]() $\mathcal {E}$
, where T is a coordinate of
$\mathcal {E}$
, where T is a coordinate of
![]() $\mathbb {P}_{\mathbb {Q}}^1$
. The Mordell–Weil theorem for function fields (see [Reference Silverman16, page 230]) asserts that
$\mathbb {P}_{\mathbb {Q}}^1$
. The Mordell–Weil theorem for function fields (see [Reference Silverman16, page 230]) asserts that
![]() $E(\mathbb {Q}(T))$
is a finitely generated group.
$E(\mathbb {Q}(T))$
is a finitely generated group.
Denote by r the rank of the generic fibre
![]() $E/\mathbb {Q}(T)$
of
$E/\mathbb {Q}(T)$
of
![]() $\mathcal {E}$
and by
$\mathcal {E}$
and by
![]() $r_t$
the rank of the specialisation
$r_t$
the rank of the specialisation
![]() $E_t/\mathbb {Q}$
of
$E_t/\mathbb {Q}$
of
![]() $\mathcal {E}$
at
$\mathcal {E}$
at
![]() $T=t$
, provided that
$T=t$
, provided that
![]() $E_t/\mathbb {Q}$
is an elliptic curve. It follows from a theorem of Silverman (see [Reference Silverman14, Theorem C] or [Reference Silverman16, Theorem III.11.4]) that
$E_t/\mathbb {Q}$
is an elliptic curve. It follows from a theorem of Silverman (see [Reference Silverman14, Theorem C] or [Reference Silverman16, Theorem III.11.4]) that
![]() $r \leq r_t$
for all but finitely many t. A natural question to ask is how far the above inequality is from being an equality. Assume from now on that
$r \leq r_t$
for all but finitely many t. A natural question to ask is how far the above inequality is from being an equality. Assume from now on that
![]() $\pi : \mathcal {E} \rightarrow \mathbb {P}_{\mathbb {Q}}^1$
is nonisotrivial. Let
$\pi : \mathcal {E} \rightarrow \mathbb {P}_{\mathbb {Q}}^1$
is nonisotrivial. Let
and
The density conjecture (see [Reference Silverman15, page 556] or [Reference Conrad, Conrad and Helfgott4, Appendix A]) predicts that
![]() $\mathcal {N}(\mathcal {E})$
is infinite while
$\mathcal {N}(\mathcal {E})$
is infinite while
![]() $\mathcal {F}(\mathcal {E})$
has density zero.
$\mathcal {F}(\mathcal {E})$
has density zero.
Proving either of these two statements at the moment seems to be out of reach. Moreover, not a single (unconditional) example of a nonisotrivial elliptic surface for which
![]() $\mathcal {N}(E)$
is infinite is known. However, conditional examples relying on standard conjectures in analytic number theory have been found. For instance, under the assumption that there are infinitely many Mersenne primes, Caro and Pasten in [Reference Caro and Pasten3] found an elliptic curve
$\mathcal {N}(E)$
is infinite is known. However, conditional examples relying on standard conjectures in analytic number theory have been found. For instance, under the assumption that there are infinitely many Mersenne primes, Caro and Pasten in [Reference Caro and Pasten3] found an elliptic curve
![]() $E/\mathbb {Q}(T)$
of rank
$E/\mathbb {Q}(T)$
of rank
![]() $0$
and infinitely many primes q such that
$0$
and infinitely many primes q such that
![]() $E_q/\mathbb {Q}$
has rank
$E_q/\mathbb {Q}$
has rank
![]() $0$
as well. Moreover, work of Neuman and Setzer (see [Reference Neumann11, Reference Setzer13]) on elliptic curves with prime conductor combined with a conjecture of Bouniakowsky [Reference Bouniakowsky2] provides another such example.
$0$
as well. Moreover, work of Neuman and Setzer (see [Reference Neumann11, Reference Setzer13]) on elliptic curves with prime conductor combined with a conjecture of Bouniakowsky [Reference Bouniakowsky2] provides another such example.
For every
![]() $i \geq 1$
, we let
$i \geq 1$
, we let
In this article, we are interested in providing examples of elliptic surfaces and explicit positive integers i such that
![]() $\mathcal {I}_i(E)$
is infinite. Our first result is the following theorem (see Theorems 2.3 and 2.4 below).
$\mathcal {I}_i(E)$
is infinite. Our first result is the following theorem (see Theorems 2.3 and 2.4 below).
Theorem 1.1. Let
![]() $E/\mathbb {Q}(T)$
be either the elliptic curve given by the Weierstrass equation
$E/\mathbb {Q}(T)$
be either the elliptic curve given by the Weierstrass equation
or the elliptic curve given by the Weierstrass equation
Then, there exist infinitely many integers n such that
![]() $\mathrm {rk } \: E_n(\mathbb {Q}) \leq 1. $
In particular, the set
$\mathrm {rk } \: E_n(\mathbb {Q}) \leq 1. $
In particular, the set
![]() $\mathcal {I}_1(E)$
is infinite.
$\mathcal {I}_1(E)$
is infinite.
Before we state our next theorem, we need to introduce some notation. If
![]() $F(x)$
is an irreducible polynomial with integer coefficients, then we write
$F(x)$
is an irreducible polynomial with integer coefficients, then we write
![]() $\rho _F(p)$
for the number of solutions of the congruence
$\rho _F(p)$
for the number of solutions of the congruence
Theorem 1.2. Let
![]() $E/\mathbb {Q}(T)$
be a nonisotrivial elliptic curve whose Mordell–Weil group contains a point of order
$E/\mathbb {Q}(T)$
be a nonisotrivial elliptic curve whose Mordell–Weil group contains a point of order
![]() $2$
. Fix an integral Weierstrass equation for
$2$
. Fix an integral Weierstrass equation for
![]() $E/\mathbb {Q}(T)$
and denote by
$E/\mathbb {Q}(T)$
and denote by
![]() $\Delta (T) \in \mathbb {Z}[T]$
its discriminant.
$\Delta (T) \in \mathbb {Z}[T]$
its discriminant.
-
(1) Assume that
 $\Delta (T)=p_1^{a_1} \cdots p_m^{a_m} f(T)^k$
, where
$\Delta (T)=p_1^{a_1} \cdots p_m^{a_m} f(T)^k$
, where
 $m \geq 0$
,
$m \geq 0$
,
 $k, a_1,\ldots ,a_m>0$
, and
$k, a_1,\ldots ,a_m>0$
, and
 $f(T)$
is an irreducible polynomial with integral coefficients such that
$f(T)$
is an irreducible polynomial with integral coefficients such that
 $\rho _{f}(p)<p$
for every prime p. Then, there exist infinitely many positive integers n such that
$\rho _{f}(p)<p$
for every prime p. Then, there exist infinitely many positive integers n such that  $$ \begin{align*}\mathrm{rk } \: E_n(\mathbb{Q}) \leq 2\deg(\Delta)+2m+1. \end{align*} $$
$$ \begin{align*}\mathrm{rk } \: E_n(\mathbb{Q}) \leq 2\deg(\Delta)+2m+1. \end{align*} $$
In particular, the set
 $\mathcal {I}_{2\deg (\Delta )+2m+1}(E)$
is infinite.
$\mathcal {I}_{2\deg (\Delta )+2m+1}(E)$
is infinite. -
(2) Assume that
 $\Delta (T)=p_1^{a_1} \cdots p_m^{a_m}T^{k_1}f(T)^{k_2}$
, where
$\Delta (T)=p_1^{a_1} \cdots p_m^{a_m}T^{k_1}f(T)^{k_2}$
, where
 $m \geq 0$
,
$m \geq 0$
,
 $k_1,k_2,a_1,\ldots ,a_m>0$
, and
$k_1,k_2,a_1,\ldots ,a_m>0$
, and
 $f(T) \neq \pm T$
is an irreducible polynomial with
$f(T) \neq \pm T$
is an irreducible polynomial with
 $\rho _{f}(p)<p$
for every prime p. Assume also that
$\rho _{f}(p)<p$
for every prime p. Assume also that
 $\rho _{f}(p)<p-1$
for every prime
$\rho _{f}(p)<p-1$
for every prime
 $p \leq \deg (f)+1$
such that
$p \leq \deg (f)+1$
such that
 $p \nmid f(0)$
. Then, there exist infinitely many positive integers n such that
$p \nmid f(0)$
. Then, there exist infinitely many positive integers n such that  $$ \begin{align*}\mathrm{rk } \: E_n(\mathbb{Q}) \leq 4\deg(f)+2m+2. \end{align*} $$
$$ \begin{align*}\mathrm{rk } \: E_n(\mathbb{Q}) \leq 4\deg(f)+2m+2. \end{align*} $$
In particular, the set
 $\mathcal {I}_{4\deg (f)+2m+2}(E)$
is infinite.
$\mathcal {I}_{4\deg (f)+2m+2}(E)$
is infinite.
In fact, we prove a more general theorem where we also treat the general case where
![]() $\Delta (T)$
factors into a product of any number of irreducible polynomials. To prove our results, we combine a bound on ranks of elliptic curves over
$\Delta (T)$
factors into a product of any number of irreducible polynomials. To prove our results, we combine a bound on ranks of elliptic curves over
![]() $\mathbb {Q}$
that depends on their discriminants coming from
$\mathbb {Q}$
that depends on their discriminants coming from
![]() $2$
-descent (see [Reference Aguirre, Lozano-Robledo and Peral1, Reference Caro and Pasten3]) with results on almost prime values of polynomials that are derived from sieve methods in analytic number theory (see, for example, [Reference Friedlander and Iwaniec5] or [Reference Halberstam and Richert6]).
$2$
-descent (see [Reference Aguirre, Lozano-Robledo and Peral1, Reference Caro and Pasten3]) with results on almost prime values of polynomials that are derived from sieve methods in analytic number theory (see, for example, [Reference Friedlander and Iwaniec5] or [Reference Halberstam and Richert6]).
2 Proofs of Theorems 1.1 and 1.2
In this section, we prove Theorems 1.1 and 1.2. In fact, we will prove more general versions of the theorems stated in the introduction. Before we begin our proofs, let us recall a theorem that provides an upper bound for the rank of elliptic curves with a torsion point of order
![]() $2$
.
$2$
.
Theorem 2.1 (See [Reference Aguirre, Lozano-Robledo and Peral1, Proposition 1.1] and [Reference Caro and Pasten3, Theorem 2.3]).
Let
![]() $E/\mathbb {Q}$
be an elliptic curve that has a point of order
$E/\mathbb {Q}$
be an elliptic curve that has a point of order
![]() $2$
.
$2$
.
-
(1) If
 $E/\mathbb {Q}$
has an integral Weierstrass equation of the form
$E/\mathbb {Q}$
has an integral Weierstrass equation of the form
 $y^2=x^3+Ax^2+Bx$
, then where
$y^2=x^3+Ax^2+Bx$
, then where $$ \begin{align*}\mathrm{rk} \: E(\mathbb{Q}) \leq \nu(A^2-4B)+\nu(B)-1,\end{align*} $$
$$ \begin{align*}\mathrm{rk} \: E(\mathbb{Q}) \leq \nu(A^2-4B)+\nu(B)-1,\end{align*} $$
 $\nu (n)$
denotes the number of positive prime divisors of a nonzero integer n.
$\nu (n)$
denotes the number of positive prime divisors of a nonzero integer n.
-
(2) Let
 $\alpha $
and
$\alpha $
and
 $\mu $
be the number of places of additive and of multiplicative reduction of
$\mu $
be the number of places of additive and of multiplicative reduction of
 $E/\mathbb {Q}$
, respectively. Then,
$E/\mathbb {Q}$
, respectively. Then,  $$ \begin{align*}\mathrm{rk} \: E(\mathbb{Q}) \leq 2\alpha+\mu-1.\end{align*} $$
$$ \begin{align*}\mathrm{rk} \: E(\mathbb{Q}) \leq 2\alpha+\mu-1.\end{align*} $$
Remark 2.2. Elliptic curves for which the inequality of part (1) of Theorem 2.1 is an equality are called elliptic curves of maximal Mordell–Weil rank. Examples of such curves have been exhibited by Aguirre et al. in [Reference Aguirre, Lozano-Robledo and Peral1].
Throughout the rest of this section, we will denote by
![]() $P_r$
the set of positive integers with at most r prime divisors, counted with multiplicity. We are now ready to proceed to the proof of Theorem 1.1 for one of the two elliptic curves.
$P_r$
the set of positive integers with at most r prime divisors, counted with multiplicity. We are now ready to proceed to the proof of Theorem 1.1 for one of the two elliptic curves.
Theorem 2.3. Consider the elliptic curve
![]() $E/\mathbb {Q}(T)$
given by
$E/\mathbb {Q}(T)$
given by
![]() $y^2=x^3+Tx^2-x$
. Then, there exist infinitely many integers n such that
$y^2=x^3+Tx^2-x$
. Then, there exist infinitely many integers n such that
![]() $E_n/\mathbb {Q}$
has Mordell–Weil rank at most
$E_n/\mathbb {Q}$
has Mordell–Weil rank at most
![]() $1$
. Moreover, there exists a positive constant C such that, if X is sufficiently large,
$1$
. Moreover, there exists a positive constant C such that, if X is sufficiently large,
 $$ \begin{align*}\#\{n : n \leq X \text{ and } \: \mathrm{rk } \: E_n(\mathbb{Q}) \leq 1 \} \geq C \frac{X}{\log X}.\end{align*} $$
$$ \begin{align*}\#\{n : n \leq X \text{ and } \: \mathrm{rk } \: E_n(\mathbb{Q}) \leq 1 \} \geq C \frac{X}{\log X}.\end{align*} $$
Proof. For an integer n, consider the elliptic curve
![]() $E_n/\mathbb {Q}$
given by
$E_n/\mathbb {Q}$
given by
![]() $y^2=x^3+nx^2-x$
. We first show that there exist infinitely many n such that
$y^2=x^3+nx^2-x$
. We first show that there exist infinitely many n such that
![]() $E_n/\mathbb {Q}$
has Mordell–Weil rank at most
$E_n/\mathbb {Q}$
has Mordell–Weil rank at most
![]() $1$
. Since
$1$
. Since
![]() $E/\mathbb {Q}(T)$
has a torsion point of order
$E/\mathbb {Q}(T)$
has a torsion point of order
![]() $2$
and the torsion subgroup of
$2$
and the torsion subgroup of
![]() $E(\mathbb {Q}(T))$
injects in
$E(\mathbb {Q}(T))$
injects in
![]() $E_n(\mathbb {Q})$
when
$E_n(\mathbb {Q})$
when
![]() $E_n/\mathbb {Q}$
is nonsingular,
$E_n/\mathbb {Q}$
is nonsingular,
![]() $E_n/\mathbb {Q}$
has a point of order
$E_n/\mathbb {Q}$
has a point of order
![]() $2$
for all but finitely many n. Therefore, it follows from part (1) of Theorem 2.1 that
$2$
for all but finitely many n. Therefore, it follows from part (1) of Theorem 2.1 that
where
![]() $\nu (N)$
denotes the number of positive prime divisors of a nonzero integer N.
$\nu (N)$
denotes the number of positive prime divisors of a nonzero integer N.
If we can find infinitely many n such that
![]() $n^2+4\in P_2$
, then we are done. In contrast, for every prime p, we have
$n^2+4\in P_2$
, then we are done. In contrast, for every prime p, we have
![]() $\rho _{n^2+4}(p) \leq 2$
and
$\rho _{n^2+4}(p) \leq 2$
and
![]() $\rho _{n^2+4}(2)=1$
, so that
$\rho _{n^2+4}(2)=1$
, so that
 $$ \begin{align*}\Gamma_{n^2+4}= \prod_{p \text{ prime}} \frac{1-\rho_{n^2+4}(p)/p}{1 -1/p}>0.\end{align*} $$
$$ \begin{align*}\Gamma_{n^2+4}= \prod_{p \text{ prime}} \frac{1-\rho_{n^2+4}(p)/p}{1 -1/p}>0.\end{align*} $$
Therefore, it follows from [Reference Lemke Oliver10] that there exist infinitely many positive integers n such that
![]() $n^2+4$
has at most two prime divisors, counted with multiplicity. This proves that there exist infinitely many positive integers n such that
$n^2+4$
has at most two prime divisors, counted with multiplicity. This proves that there exist infinitely many positive integers n such that
![]() $E_n/\mathbb {Q}$
has Mordell–Weil rank at most
$E_n/\mathbb {Q}$
has Mordell–Weil rank at most
![]() $1$
.
$1$
.
We now show the inequality of the theorem. Consider the polynomial
According to [Reference Kapoor9, Theorem 1] (see also [Reference Iwaniec8, page 172] and [Reference Lemke Oliver10]), if X is sufficiently large,
 $$ \begin{align*}\# \{n' : n' \leq X \text{ and } h(n') \in P_2 \} \geq \frac{1}{144}\prod_{p \text{ prime}} \frac{1-\rho_{h}(p)/p}{1 -1/p}\frac{X}{\log X}.\end{align*} $$
$$ \begin{align*}\# \{n' : n' \leq X \text{ and } h(n') \in P_2 \} \geq \frac{1}{144}\prod_{p \text{ prime}} \frac{1-\rho_{h}(p)/p}{1 -1/p}\frac{X}{\log X}.\end{align*} $$
Further,
Therefore,
 $$ \begin{align*}\# \{n : n \leq X \text{ and } n^2+4 \in P_2 \} \geq \frac{1}{144}\prod_{p \text{ prime}} \frac{1-\rho_{h}(p)/p}{1 -1/p}\frac{X}{\log X} -1 \geq C \frac{X}{\log X}\end{align*} $$
$$ \begin{align*}\# \{n : n \leq X \text{ and } n^2+4 \in P_2 \} \geq \frac{1}{144}\prod_{p \text{ prime}} \frac{1-\rho_{h}(p)/p}{1 -1/p}\frac{X}{\log X} -1 \geq C \frac{X}{\log X}\end{align*} $$
for all X sufficiently large (picking an appropriate constant C). This proves our theorem.
Consider now the elliptic curve
![]() $E/\mathbb {Q}(T)$
given by the Weierstrass equation
$E/\mathbb {Q}(T)$
given by the Weierstrass equation
Specialisations of this curve have been studied by Neumann [Reference Neumann11] and Setzer [Reference Setzer13]. More precisely, it is proved in [Reference Setzer13, Theorem 2] that if
![]() $p \neq 2,3,17$
is a prime and
$p \neq 2,3,17$
is a prime and
![]() $E/\mathbb {Q}$
is an elliptic curve of conductor p with a torsion point of order
$E/\mathbb {Q}$
is an elliptic curve of conductor p with a torsion point of order
![]() $2$
, then
$2$
, then
![]() $p=b^2+64$
for some integer
$p=b^2+64$
for some integer
![]() $b \equiv 1 \: (\text {mod } 4)$
. In this case,
$b \equiv 1 \: (\text {mod } 4)$
. In this case,
![]() $E/\mathbb {Q}$
is isomorphic to either the curve
$E/\mathbb {Q}$
is isomorphic to either the curve
![]() $E_b/\mathbb {Q}$
or to a curve which is isogenous to
$E_b/\mathbb {Q}$
or to a curve which is isogenous to
![]() $E_b/\mathbb {Q}$
.
$E_b/\mathbb {Q}$
.
It follows from part (2) of Theorem 2.1 that if p is a prime of the form
![]() $p=b^2+64$
for some integer
$p=b^2+64$
for some integer
![]() $b \equiv 1 \: (\text {mod } 4)$
, then the specialisation
$b \equiv 1 \: (\text {mod } 4)$
, then the specialisation
![]() $E_b/\mathbb {Q}$
has rank equal to
$E_b/\mathbb {Q}$
has rank equal to
![]() $0$
. According to a conjecture of Bouniakowsky [Reference Bouniakowsky2, page 328], there are infinitely many such numbers b. Without relying on any conjectures, we show below that we can find infinitely many integers n such that
$0$
. According to a conjecture of Bouniakowsky [Reference Bouniakowsky2, page 328], there are infinitely many such numbers b. Without relying on any conjectures, we show below that we can find infinitely many integers n such that
![]() $n^2+64 \in P_2$
, which forces the rank of the corresponding curve
$n^2+64 \in P_2$
, which forces the rank of the corresponding curve
![]() $E_n/\mathbb {Q}$
to be at most
$E_n/\mathbb {Q}$
to be at most
![]() $1$
.
$1$
.
Theorem 2.4. Consider the elliptic curve
![]() $E/\mathbb {Q}(T)$
given by
$E/\mathbb {Q}(T)$
given by
Then, there exist infinitely many integers n such that
![]() $E_n/\mathbb {Q}$
has Mordell–Weil rank at most
$E_n/\mathbb {Q}$
has Mordell–Weil rank at most
![]() $1$
.
$1$
.
Proof. The proof is similar to the proof of Theorem 2.3. For every
![]() $n\in \mathbb {Z}$
, consider the elliptic curve
$n\in \mathbb {Z}$
, consider the elliptic curve
![]() $E_n/\mathbb {Q}$
given by
$E_n/\mathbb {Q}$
given by
The discriminant of
![]() $E_n/\mathbb {Q}$
is
$E_n/\mathbb {Q}$
is
![]() $\Delta (n)=n^2+64$
and the
$\Delta (n)=n^2+64$
and the
![]() $c_4$
-invariant is
$c_4$
-invariant is
![]() $c_4(n)=n^2+48$
. Since
$c_4(n)=n^2+48$
. Since
![]() $E/\mathbb {Q}(T)$
has a torsion point of order
$E/\mathbb {Q}(T)$
has a torsion point of order
![]() $2$
, we find that
$2$
, we find that
![]() $E_n/\mathbb {Q}$
has a point of order
$E_n/\mathbb {Q}$
has a point of order
![]() $2$
for all but finitely many
$2$
for all but finitely many
![]() $E_n/\mathbb {Q}$
. The strategy that we will follow for the rest of the proof is to try to control the primes of bad reduction of
$E_n/\mathbb {Q}$
. The strategy that we will follow for the rest of the proof is to try to control the primes of bad reduction of
![]() $E_n/\mathbb {Q}$
for sufficiently many integers n and apply Theorem 2.1.
$E_n/\mathbb {Q}$
for sufficiently many integers n and apply Theorem 2.1.
Claim 2.5. If
![]() $n^2+64 \in P_2$
, then n is odd.
$n^2+64 \in P_2$
, then n is odd.
Proof of the claim.
If
![]() $n^2+64$
is odd, then n must be odd. Therefore, assume that
$n^2+64$
is odd, then n must be odd. Therefore, assume that
where q is a prime (not necessarily distinct from
![]() $2$
). This means that n is even. If we write
$2$
). This means that n is even. If we write
![]() $n=2n'$
, then
$n=2n'$
, then
and we see that q is even, so
![]() $q=2$
. However, then
$q=2$
. However, then
![]() $n^2+64=4,$
which is impossible. Therefore, n must be odd.
$n^2+64=4,$
which is impossible. Therefore, n must be odd.
If
![]() $n^2+64 \in P_2$
, then
$n^2+64 \in P_2$
, then
![]() $n^2+64$
is odd and, hence, n is odd. Moreover, by replacing n with
$n^2+64$
is odd and, hence, n is odd. Moreover, by replacing n with
![]() $-n$
if necessary, we can also arrange that
$-n$
if necessary, we can also arrange that
![]() $n \equiv 1\: (\text {mod } 4).$
Thus, the given Weierstrass equation for
$n \equiv 1\: (\text {mod } 4).$
Thus, the given Weierstrass equation for
![]() $E_n/\mathbb {Q}$
is an integral Weierstrass equation and by looking at the corresponding
$E_n/\mathbb {Q}$
is an integral Weierstrass equation and by looking at the corresponding
![]() $c_4$
-invariant, we see that when
$c_4$
-invariant, we see that when
![]() $n^2+64 \in P_2$
, every divisor of
$n^2+64 \in P_2$
, every divisor of
![]() $\Delta (n)$
does not divide
$\Delta (n)$
does not divide
![]() $c_4(n)$
. This proves that if
$c_4(n)$
. This proves that if
![]() $n^2+64 \in P_2$
, then the curve
$n^2+64 \in P_2$
, then the curve
![]() $E_n/\mathbb {Q}$
has at most two primes of multiplicative reduction and no primes of additive reduction. Therefore, it follows from part (2) of Theorem 2.1 that
$E_n/\mathbb {Q}$
has at most two primes of multiplicative reduction and no primes of additive reduction. Therefore, it follows from part (2) of Theorem 2.1 that
where
![]() $\mu _n \leq 2$
is the number of primes of multiplicative reduction of
$\mu _n \leq 2$
is the number of primes of multiplicative reduction of
![]() $E_n/\mathbb {Q}$
. This shows that when
$E_n/\mathbb {Q}$
. This shows that when
![]() $n^2+64 \in P_2$
, we have
$n^2+64 \in P_2$
, we have
![]() $\mathrm {rk} \: E_n(\mathbb {Q}) \leq 1$
.
$\mathrm {rk} \: E_n(\mathbb {Q}) \leq 1$
.
Since
![]() $\rho _{n^2+64}(p) \leq 2$
and
$\rho _{n^2+64}(p) \leq 2$
and
![]() $\rho _{n^2+64}(2)=1$
for every prime p,
$\rho _{n^2+64}(2)=1$
for every prime p,
 $$ \begin{align*}\Gamma_{n^2+64}= \prod_{p \text{ prime}} \frac{1-\rho_{n^2+64}(p)/p}{1 -1/p}>0.\end{align*} $$
$$ \begin{align*}\Gamma_{n^2+64}= \prod_{p \text{ prime}} \frac{1-\rho_{n^2+64}(p)/p}{1 -1/p}>0.\end{align*} $$
Therefore, it follows from [Reference Lemke Oliver10] that there exist infinitely many n such that
![]() $n^2+64 \in P_2$
. Hence, there exist infinitely many integers n such that
$n^2+64 \in P_2$
. Hence, there exist infinitely many integers n such that
![]() $\mathrm {rk} \: E_n(\mathbb {Q}) \leq 1$
.
$\mathrm {rk} \: E_n(\mathbb {Q}) \leq 1$
.
Before we proceed to the proof of a slightly more general version of Theorem 1.2, we need to recall two theorems on almost-prime values of polynomials that are derived from analytic number theory and will be needed in our proofs.
Theorem 2.6 ([Reference Richert12, Theorem 6] and [Reference Richert12, Theorem 7]).
Let
![]() $F(x)$
be an irreducible polynomial of degree
$F(x)$
be an irreducible polynomial of degree
![]() $g \geq 1$
with integral coefficients. Assume that
$g \geq 1$
with integral coefficients. Assume that
![]() $\rho _F(p)<p$
for every prime p.
$\rho _F(p)<p$
for every prime p.
-
(1) Then, there exists a constant
 $X_0(F)$
that depends on F such that for every
$X_0(F)$
that depends on F such that for every
 ${X \geq X_0(F)}$
,
${X \geq X_0(F)}$
,  $$ \begin{align*}\#\{n : 1 \leq n \leq X, F(n) \in P_{g+1} \} \geq \frac{2}{3} \prod_p \frac{1-\rho_{F}(p)/p}{1 -1/p} \frac{X}{\log(X)}.\end{align*} $$
$$ \begin{align*}\#\{n : 1 \leq n \leq X, F(n) \in P_{g+1} \} \geq \frac{2}{3} \prod_p \frac{1-\rho_{F}(p)/p}{1 -1/p} \frac{X}{\log(X)}.\end{align*} $$
In particular, there exist infinitely many integers n such that
 $F(n)$
has at most
$F(n)$
has at most
 $g+1$
prime factors.
$g+1$
prime factors. -
(2) Assume in addition that
 $\rho _{F}(p)<p-1$
for every prime
$\rho _{F}(p)<p-1$
for every prime
 $p \leq \deg (F)+1$
with
$p \leq \deg (F)+1$
with
 ${p \nmid F(0)}$
. Then, there exist positive constants
${p \nmid F(0)}$
. Then, there exist positive constants
 $C(F)$
and
$C(F)$
and
 $X_0(F)$
that depend on F such that for every
$X_0(F)$
that depend on F such that for every
 $X \geq X_0(F)$
,
$X \geq X_0(F)$
,  $$ \begin{align*}\#\{ p \text{ prime } : 1 \leq p \leq X, F(p) \in P_{2g+1} \} \geq C(F) \frac{X}{\log^2(X)}.\end{align*} $$
$$ \begin{align*}\#\{ p \text{ prime } : 1 \leq p \leq X, F(p) \in P_{2g+1} \} \geq C(F) \frac{X}{\log^2(X)}.\end{align*} $$
In particular, there exist infinitely many prime numbers p such that
 $F(p)$
has at most
$F(p)$
has at most
 $2g+1$
prime factors.
$2g+1$
prime factors.
Theorem 2.7 [Reference Halberstam and Richert6, Theorem 10.4].
Let
![]() $F_1(x), F_2(x),\ldots ,F_g(x) $
be distinct irreducible polynomials with integral coefficients and write
$F_1(x), F_2(x),\ldots ,F_g(x) $
be distinct irreducible polynomials with integral coefficients and write
![]() $F(x)=F_1(x)F_2(x) \cdots F_g(x)$
for their product. Assume that
$F(x)=F_1(x)F_2(x) \cdots F_g(x)$
for their product. Assume that
![]() $\rho _F(p)<p$
for every prime p. Then, there exists a positive integer s that can be explicitly computed and depends on F, and a positive constant
$\rho _F(p)<p$
for every prime p. Then, there exists a positive integer s that can be explicitly computed and depends on F, and a positive constant
![]() $C(F)$
that depends on F such that for all X sufficiently large,
$C(F)$
that depends on F such that for all X sufficiently large,
 $$ \begin{align*}\#\{n : 1 \leq n \leq X, F(n) \in P_s \} \geq C(F)\frac{X}{\log^g(X)}.\end{align*} $$
$$ \begin{align*}\#\{n : 1 \leq n \leq X, F(n) \in P_s \} \geq C(F)\frac{X}{\log^g(X)}.\end{align*} $$
We are now ready to proceed to the proof of a slightly more general version of Theorem 1.2.
Theorem 2.8. Let
![]() $E/\mathbb {Q}(T)$
be a nonisotrivial elliptic curve whose Mordell–Weil group contains a point of order
$E/\mathbb {Q}(T)$
be a nonisotrivial elliptic curve whose Mordell–Weil group contains a point of order
![]() $2$
. Fix an integral Weierstrass equation for
$2$
. Fix an integral Weierstrass equation for
![]() $E/\mathbb {Q}(T)$
and denote its discriminant by
$E/\mathbb {Q}(T)$
and denote its discriminant by
![]() $\Delta (T) \in \mathbb {Z}[T]$
.
$\Delta (T) \in \mathbb {Z}[T]$
.
-
(1) Assume that
 $\Delta (T)=p_1^{a_1} \cdots p_m^{a_m} f(T)^k$
, where
$\Delta (T)=p_1^{a_1} \cdots p_m^{a_m} f(T)^k$
, where
 $m \geq 0$
,
$m \geq 0$
,
 $k, a_1,\ldots ,a_m>0$
, and
$k, a_1,\ldots ,a_m>0$
, and
 $f(T)$
is an irreducible polynomial with integral coefficients such that
$f(T)$
is an irreducible polynomial with integral coefficients such that
 $\rho _{f}(p)<p$
for every prime p. Then, there exists a constant
$\rho _{f}(p)<p$
for every prime p. Then, there exists a constant
 $X_0(f)$
that depends only on f such that for every
$X_0(f)$
that depends only on f such that for every
 $X \geq X_0(f)$
,
$X \geq X_0(f)$
,  $$ \begin{align*}\#\{n : 1 \leq n \leq X, \mathrm{rk } \: E_n(\mathbb{Q}) \leq 2\deg(\Delta)+2m+1 \} \geq \frac{2}{3} \prod_p \frac{1-\rho_{f}(p)/p}{1 -1/p} \frac{X}{\log(X)}.\end{align*} $$
$$ \begin{align*}\#\{n : 1 \leq n \leq X, \mathrm{rk } \: E_n(\mathbb{Q}) \leq 2\deg(\Delta)+2m+1 \} \geq \frac{2}{3} \prod_p \frac{1-\rho_{f}(p)/p}{1 -1/p} \frac{X}{\log(X)}.\end{align*} $$
In particular, there exist infinitely many positive integers n such that
 $$ \begin{align*}\mathrm{rk }\ E_n(\mathbb{Q}) \leq 2\deg(\Delta)+2m+1. \end{align*} $$
$$ \begin{align*}\mathrm{rk }\ E_n(\mathbb{Q}) \leq 2\deg(\Delta)+2m+1. \end{align*} $$
-
(2) Assume that
 $\Delta (T)=p_1^{a_1} \cdots p_m^{a_m}T^{k_1}f(T)^{k_2}$
, where
$\Delta (T)=p_1^{a_1} \cdots p_m^{a_m}T^{k_1}f(T)^{k_2}$
, where
 $m \geq 0$
,
$m \geq 0$
,
 $k_1,k_2,a_1,\ldots ,a_m>0$
, and
$k_1,k_2,a_1,\ldots ,a_m>0$
, and
 $f(T) \neq \pm T$
is an irreducible polynomial with
$f(T) \neq \pm T$
is an irreducible polynomial with
 $\rho _{f}(p)<p$
for every prime p. Assume also that
$\rho _{f}(p)<p$
for every prime p. Assume also that
 $\rho _{f}(p)<p-1$
for every prime
$\rho _{f}(p)<p-1$
for every prime
 $p \leq \deg (f)+1$
with
$p \leq \deg (f)+1$
with
 $p \nmid f(0)$
. Then, there exist constants
$p \nmid f(0)$
. Then, there exist constants
 $C(f)$
and
$C(f)$
and
 $X_1(f)$
that depend only on f such that for every
$X_1(f)$
that depend only on f such that for every
 ${X \geq X_1(f)}$
,
${X \geq X_1(f)}$
,  $$ \begin{align*}\#\{n : 1 \leq n \leq X, \mathrm{rk } \: E_n(\mathbb{Q}) \leq 4\deg (f)+2m+2 \} \geq C(f)\frac{X}{\log^2(X)}.\end{align*} $$
$$ \begin{align*}\#\{n : 1 \leq n \leq X, \mathrm{rk } \: E_n(\mathbb{Q}) \leq 4\deg (f)+2m+2 \} \geq C(f)\frac{X}{\log^2(X)}.\end{align*} $$
In particular, there exist infinitely many positive integers n such that
 $$ \begin{align*}\mathrm{rk }\ E_n(\mathbb{Q}) \leq 4\deg (f)+2m+2. \end{align*} $$
$$ \begin{align*}\mathrm{rk }\ E_n(\mathbb{Q}) \leq 4\deg (f)+2m+2. \end{align*} $$
-
(3) More generally, write
 $\Delta (T)=p_1^{a_1} \cdots p_m^{a_m} f_1(T)^{h_1} \cdots f_g(T)^{h_g}$
, where
$\Delta (T)=p_1^{a_1} \cdots p_m^{a_m} f_1(T)^{h_1} \cdots f_g(T)^{h_g}$
, where
 $p_1,\ldots ,p_m$
are distinct primes for some
$p_1,\ldots ,p_m$
are distinct primes for some
 $m \geq 0$
and
$m \geq 0$
and
 $f_1(T),\ldots ,f_g(T)$
are distinct irreducible polynomials with integral coefficients for some
$f_1(T),\ldots ,f_g(T)$
are distinct irreducible polynomials with integral coefficients for some
 $g \geq 1$
. Assume that
$g \geq 1$
. Assume that
 $\rho _{f_1(T) \cdots f_g(T)}(p)<p$
for every prime p. Then, there exists a positive constant
$\rho _{f_1(T) \cdots f_g(T)}(p)<p$
for every prime p. Then, there exists a positive constant
 $C(f_1,\ldots ,f_g)$
that depends on
$C(f_1,\ldots ,f_g)$
that depends on
 $f_1,\ldots ,f_g$
such that for all X sufficiently large, where s is a positive integer that can be explicitly computed and depends on
$f_1,\ldots ,f_g$
such that for all X sufficiently large, where s is a positive integer that can be explicitly computed and depends on $$ \begin{align*}\#\{n : 1 \leq n \leq X, \mathrm{rk } \: E_n(\mathbb{Q}) \leq 2(m+s) -1 \} \geq C(f_1,\ldots,f_g) \frac{X}{\log^g(X)},\end{align*} $$
$$ \begin{align*}\#\{n : 1 \leq n \leq X, \mathrm{rk } \: E_n(\mathbb{Q}) \leq 2(m+s) -1 \} \geq C(f_1,\ldots,f_g) \frac{X}{\log^g(X)},\end{align*} $$
 $\deg \Delta (T)$
and g.
$\deg \Delta (T)$
and g.
Proof of part (1).
Let
![]() $E/\mathbb {Q}(T)$
be an elliptic curve as in part (1). Since
$E/\mathbb {Q}(T)$
be an elliptic curve as in part (1). Since
![]() $E/\mathbb {Q}(T)$
has a torsion point of order
$E/\mathbb {Q}(T)$
has a torsion point of order
![]() $2$
and the torsion subgroup of
$2$
and the torsion subgroup of
![]() $E(\mathbb {Q}(T))$
injects in
$E(\mathbb {Q}(T))$
injects in
![]() $E_t(\mathbb {Q})$
when
$E_t(\mathbb {Q})$
when
![]() $E_t/\mathbb {Q}$
is nonsingular,
$E_t/\mathbb {Q}$
is nonsingular,
![]() $E_t/\mathbb {Q}$
contains a point of order
$E_t/\mathbb {Q}$
contains a point of order
![]() $2$
for all but finitely many
$2$
for all but finitely many
![]() $E_t/\mathbb {Q}$
. Moreover, applying part (1) of Theorem 2.6 to the polynomial
$E_t/\mathbb {Q}$
. Moreover, applying part (1) of Theorem 2.6 to the polynomial
![]() $f(T)$
yields a constant
$f(T)$
yields a constant
![]() $X_0(f)$
that depends on f such that for every
$X_0(f)$
that depends on f such that for every
![]() $X \geq X_0(f)$
,
$X \geq X_0(f)$
,
 $$ \begin{align*}\#\{n : 1 \leq n \leq X, f(n) \in P_{\deg (f)+1} \} \geq \frac{2}{3} \prod_p \frac{1-\rho_{f}(p)/p}{1 -1/p} \frac{X}{\log(X)}.\end{align*} $$
$$ \begin{align*}\#\{n : 1 \leq n \leq X, f(n) \in P_{\deg (f)+1} \} \geq \frac{2}{3} \prod_p \frac{1-\rho_{f}(p)/p}{1 -1/p} \frac{X}{\log(X)}.\end{align*} $$
Recall that
![]() $\Delta (T)=p_1^{a_1} \cdots p_m^{a_m} f(T)^k$
and note that for each
$\Delta (T)=p_1^{a_1} \cdots p_m^{a_m} f(T)^k$
and note that for each
![]() $n \in \mathbb {N}$
, the primes of bad reduction of
$n \in \mathbb {N}$
, the primes of bad reduction of
![]() $E_n/\mathbb {Q}$
are a subset of the primes that divide
$E_n/\mathbb {Q}$
are a subset of the primes that divide
![]() $\Delta (n)$
. Therefore, by applying part (2) of Theorem 2.1 to each
$\Delta (n)$
. Therefore, by applying part (2) of Theorem 2.1 to each
![]() $E_n/\mathbb {Q}$
, we find that if
$E_n/\mathbb {Q}$
, we find that if
![]() $f(n) \in P_{\deg (f)+1}$
, then the rank of
$f(n) \in P_{\deg (f)+1}$
, then the rank of
![]() $E_n/\mathbb {Q}$
is at most
$E_n/\mathbb {Q}$
is at most
![]() $2(\deg (f)+1+m)-1=2\deg (f)+2m+1$
. Since
$2(\deg (f)+1+m)-1=2\deg (f)+2m+1$
. Since
![]() $\deg (f)=\deg (\Delta )$
, the proof of part (1) is complete.
$\deg (f)=\deg (\Delta )$
, the proof of part (1) is complete.
Proof of part (2).
Now, let
![]() $E/\mathbb {Q}(T)$
be an elliptic curve as in part (2). As in the previous part,
$E/\mathbb {Q}(T)$
be an elliptic curve as in part (2). As in the previous part,
![]() $E_t/\mathbb {Q}$
contains a point of order
$E_t/\mathbb {Q}$
contains a point of order
![]() $2$
for all but finitely many
$2$
for all but finitely many
![]() $E_t/\mathbb {Q}$
. Applying part (2) of Theorem 2.6 to the polynomial
$E_t/\mathbb {Q}$
. Applying part (2) of Theorem 2.6 to the polynomial
![]() $f(T)$
yields positive constants
$f(T)$
yields positive constants
![]() $C(f)$
and
$C(f)$
and
![]() $X_0(f)$
that depend on f such that for every
$X_0(f)$
that depend on f such that for every
![]() $X \geq X_0(f)$
,
$X \geq X_0(f)$
,
 $$ \begin{align*}\#\{ p \text{ prime } : 1 \leq p \leq X, f(p) \in P_{2 \deg (f)+1} \} \geq C(f) \frac{X}{\log^2(X)}.\end{align*} $$
$$ \begin{align*}\#\{ p \text{ prime } : 1 \leq p \leq X, f(p) \in P_{2 \deg (f)+1} \} \geq C(f) \frac{X}{\log^2(X)}.\end{align*} $$
Recall
![]() $\Delta (T)=p_1^{a_1} \cdots p_m^{a_m}T^{k_1}f(T)^{k_2}$
and note that for each
$\Delta (T)=p_1^{a_1} \cdots p_m^{a_m}T^{k_1}f(T)^{k_2}$
and note that for each
![]() $n \in \mathbb {N}$
, the primes of bad reduction of
$n \in \mathbb {N}$
, the primes of bad reduction of
![]() $E_n/\mathbb {Q}$
are a subset of the primes that divide
$E_n/\mathbb {Q}$
are a subset of the primes that divide
![]() $\Delta (n)$
. Therefore, by applying part (2) of Theorem 2.1 to each
$\Delta (n)$
. Therefore, by applying part (2) of Theorem 2.1 to each
![]() $E_n/\mathbb {Q}$
, we find that if n is prime with
$E_n/\mathbb {Q}$
, we find that if n is prime with
![]() $f(n) \in P_{2 \deg (f)+1}$
, then the rank of
$f(n) \in P_{2 \deg (f)+1}$
, then the rank of
![]() $E_n/\mathbb {Q}$
is at most
$E_n/\mathbb {Q}$
is at most
![]() $2(2 \deg (f) +2+m)-1=4\deg (f)+2m+2$
.
$2(2 \deg (f) +2+m)-1=4\deg (f)+2m+2$
.
Proof of part (3).
Now, let
![]() $E/\mathbb {Q}(T)$
be an elliptic curve as in part (3). As in the previous parts,
$E/\mathbb {Q}(T)$
be an elliptic curve as in part (3). As in the previous parts,
![]() $E_t/\mathbb {Q}$
contains a point of order
$E_t/\mathbb {Q}$
contains a point of order
![]() $2$
for all but finitely many
$2$
for all but finitely many
![]() $E_t/\mathbb {Q}$
. Applying Theorem 2.7 to the polynomial
$E_t/\mathbb {Q}$
. Applying Theorem 2.7 to the polynomial
![]() $f_1(T) \cdots f_g(T)$
, we find that there exists a positive integer s that can be explicitly computed, and depends on
$f_1(T) \cdots f_g(T)$
, we find that there exists a positive integer s that can be explicitly computed, and depends on
![]() $f_1(T),\ldots ,f_g(T)$
and a positive constant
$f_1(T),\ldots ,f_g(T)$
and a positive constant
![]() $C(f_1,\ldots ,f_g)$
that depends on
$C(f_1,\ldots ,f_g)$
that depends on
![]() $f_1(T),\ldots ,f_g(T)$
such that for all X sufficiently large,
$f_1(T),\ldots ,f_g(T)$
such that for all X sufficiently large,
 $$ \begin{align*}\#\{n : 1 \leq n \leq X, f_1(n) \cdots f_g(T) \in P_s \} \geq C(F)\frac{X}{\log^g(X)}.\end{align*} $$
$$ \begin{align*}\#\{n : 1 \leq n \leq X, f_1(n) \cdots f_g(T) \in P_s \} \geq C(F)\frac{X}{\log^g(X)}.\end{align*} $$
Recall that
![]() $\Delta (T)=p_1^{a_1} \cdots p_m^{a_m} f_1(T)^{h_1} \cdots f_g(T)^{h_g}$
and note that for each
$\Delta (T)=p_1^{a_1} \cdots p_m^{a_m} f_1(T)^{h_1} \cdots f_g(T)^{h_g}$
and note that for each
![]() $n \in \mathbb {N}$
, the primes of bad reduction of
$n \in \mathbb {N}$
, the primes of bad reduction of
![]() $E_n/\mathbb {Q}$
are a subset of the primes that divide
$E_n/\mathbb {Q}$
are a subset of the primes that divide
![]() $\Delta (n)$
. Therefore, by applying part (2) of Theorem 2.1 to each
$\Delta (n)$
. Therefore, by applying part (2) of Theorem 2.1 to each
![]() $E_n/\mathbb {Q}$
, we find that if n is prime with
$E_n/\mathbb {Q}$
, we find that if n is prime with
![]() $f(n) \in P_{2 \deg (f)+1}$
, then the rank of
$f(n) \in P_{2 \deg (f)+1}$
, then the rank of
![]() $E_n/\mathbb {Q}$
is at most
$E_n/\mathbb {Q}$
is at most
![]() $2(s+m)-1=2s+2m-1$
. This completes the proof of our theorem.
$2(s+m)-1=2s+2m-1$
. This completes the proof of our theorem.
We end this article by presenting some examples where Theorem 2.8 can be applied to find explicit bounds for the ranks of infinitely many specialisations.
Example 2.9. Consider the elliptic curve
![]() $E/\mathbb {Q}(T)$
given
$E/\mathbb {Q}(T)$
given
![]() $y^2=x^3+g(T)x^2-\lambda x$
, where
$y^2=x^3+g(T)x^2-\lambda x$
, where
![]() $g(T) \in \mathbb {Z}[T]$
and
$g(T) \in \mathbb {Z}[T]$
and
![]() $\lambda $
is a positive integer. This elliptic curve has discriminant
$\lambda $
is a positive integer. This elliptic curve has discriminant
When
![]() $g(T)^2+4\lambda $
is an irreducible polynomial such that
$g(T)^2+4\lambda $
is an irreducible polynomial such that
![]() $\rho _g(p)<p$
for every prime p, part (1) of Theorem 2.8 shows that there exist infinitely many positive integers n such that
$\rho _g(p)<p$
for every prime p, part (1) of Theorem 2.8 shows that there exist infinitely many positive integers n such that
![]() $\mathrm {rk } E_n(\mathbb {Q}) \leq 4\deg (g)+2v(\lambda )+3$
, where
$\mathrm {rk } E_n(\mathbb {Q}) \leq 4\deg (g)+2v(\lambda )+3$
, where
![]() $v(\lambda )$
is the number of positive prime divisors of
$v(\lambda )$
is the number of positive prime divisors of
![]() $\lambda $
.
$\lambda $
.
Example 2.10. Consider the elliptic curve
![]() $E/\mathbb {Q}(T)$
given by
$E/\mathbb {Q}(T)$
given by
![]() $y^2+xy-Ty=x^3-Tx^2$
, which has discriminant
$y^2+xy-Ty=x^3-Tx^2$
, which has discriminant
![]() $\Delta (T)=T^4(1+16T)$
. It is well known (see [Reference Husemöller7, Section 4.4]) that if
$\Delta (T)=T^4(1+16T)$
. It is well known (see [Reference Husemöller7, Section 4.4]) that if
![]() $E'/\mathbb {Q}$
is any elliptic curve with a torsion point of order
$E'/\mathbb {Q}$
is any elliptic curve with a torsion point of order
![]() $4$
, then there exists
$4$
, then there exists
![]() $\lambda \in \mathbb {Q}$
such that
$\lambda \in \mathbb {Q}$
such that
![]() $E'/\mathbb {Q}$
is isomorphic to
$E'/\mathbb {Q}$
is isomorphic to
![]() $E_{\lambda }/\mathbb {Q}$
. According to part (2) of Theorem 2.8, there exist infinitely many integers n such that the rank of
$E_{\lambda }/\mathbb {Q}$
. According to part (2) of Theorem 2.8, there exist infinitely many integers n such that the rank of
![]() $E_n/\mathbb {Q}$
is at most
$E_n/\mathbb {Q}$
is at most
![]() $6$
. It is easy to check that the discriminant of
$6$
. It is easy to check that the discriminant of
![]() $E/\mathbb {Q}(T)$
satisfies the hypotheses of part (2) of Theorem 2.8.
$E/\mathbb {Q}(T)$
satisfies the hypotheses of part (2) of Theorem 2.8.
Remark 2.11. Keep the same notation as in Theorem 2.8. Given an elliptic curve that satisfies the conditions of part (3) of Theorem 2.8, the corresponding number s can be explicitly computed. A formula for s can be found on [Reference Halberstam and Richert6, page 283]. In the simple case where
![]() $g=2$
, that is, when
$g=2$
, that is, when
such an s can be computed based only on the degree of
![]() $\Delta (T).$
For example, when
$\Delta (T).$
For example, when
![]() $\deg (\Delta (T))$
is equal to
$\deg (\Delta (T))$
is equal to
![]() $3,4,5$
or
$3,4,5$
or
![]() $6$
, then s is equal to
$6$
, then s is equal to
![]() $7,9,10$
or
$7,9,10$
or
![]() $11$
, respectively (see [Reference Halberstam and Richert6, page 287]).
$11$
, respectively (see [Reference Halberstam and Richert6, page 287]).
Example 2.12. Consider the elliptic curve
![]() $E/\mathbb {Q}(T)$
given by
$E/\mathbb {Q}(T)$
given by
![]() $y^2=x^3+(T+1)x^2-(T^2+1)x$
which has discriminant
$y^2=x^3+(T+1)x^2-(T^2+1)x$
which has discriminant
By part (3) of Theorem 2.8 combined with Remark 2.11, there exist infinitely many n such that the rank of
![]() $E_n/\mathbb {Q}$
is at most
$E_n/\mathbb {Q}$
is at most
![]() $9$
.
$9$
.
Acknowledgement
I would like to thank the anonymous referee for a fast review and a very helpful correction.