Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Singha, Boorapa
Sanwong, Jintana
and
Sullivan, Robert Patrick
2012.
INJECTIVE PARTIAL TRANSFORMATIONS WITH INFINITE DEFECTS.
Bulletin of the Korean Mathematical Society,
Vol. 49,
Issue. 1,
p.
109.
MENDES ARAÚJO, C.
and
MENDES-GONÇALVES, S.
2022.
INJECTIVE LINEAR TRANSFORMATIONS WITH EQUAL GAP AND DEFECT.
Bulletin of the Australian Mathematical Society,
Vol. 105,
Issue. 1,
p.
106.
MENDES-GONÇALVES, SUZANA
and
SULLIVAN, R. P.
2024.
MAXIMAL SUBSEMIGROUPS OF INFINITE SYMMETRIC GROUPS.
Bulletin of the Australian Mathematical Society,
Vol. 110,
Issue. 2,
p.
324.

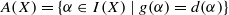 . For example, we describe Green’s relations and ideals in
. For example, we describe Green’s relations and ideals in 