Article contents
IMAGES OF HIGHER-ORDER DIFFERENTIAL OPERATORS OF POLYNOMIAL ALGEBRAS
Published online by Cambridge University Press: 09 June 2017
Abstract
We investigate images of higher-order differential operators of polynomial algebras over a field 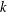 $k$ . We show that, when
$k$ . We show that, when 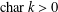 $\operatorname{char}k>0$ , the image of the set of differential operators
$\operatorname{char}k>0$ , the image of the set of differential operators 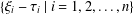 $\{\unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D70F}_{i}\mid i=1,2,\ldots ,n\}$ of the polynomial algebra
$\{\unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D70F}_{i}\mid i=1,2,\ldots ,n\}$ of the polynomial algebra 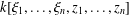 $k[\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{n},z_{1},\ldots ,z_{n}]$ is a Mathieu subspace, where
$k[\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{n},z_{1},\ldots ,z_{n}]$ is a Mathieu subspace, where 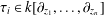 $\unicode[STIX]{x1D70F}_{i}\in k[\unicode[STIX]{x2202}_{z_{1}},\ldots ,\unicode[STIX]{x2202}_{z_{n}}]$ for
$\unicode[STIX]{x1D70F}_{i}\in k[\unicode[STIX]{x2202}_{z_{1}},\ldots ,\unicode[STIX]{x2202}_{z_{n}}]$ for 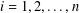 $i=1,2,\ldots ,n$ . We also show that, when
$i=1,2,\ldots ,n$ . We also show that, when 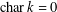 $\operatorname{char}k=0$ , the same conclusion holds for
$\operatorname{char}k=0$ , the same conclusion holds for 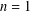 $n=1$ . The problem concerning images of differential operators arose from the study of the Jacobian conjecture.
$n=1$ . The problem concerning images of differential operators arose from the study of the Jacobian conjecture.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 96 , Issue 2 , October 2017 , pp. 205 - 211
- Copyright
- © 2017 Australian Mathematical Publishing Association Inc.
Footnotes
This work was supported by the NSF of China (11401249, 11371165) and the STDPF of Jilin Province, China (20150520051JH, 20150101001JC).
References
- 2
- Cited by

