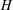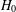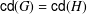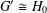Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shirjian, Farrokh
and
Iranmanesh, Ali
2020.
Extending Huppert’s conjecture to almost simple groups of Lie type.
Illinois Journal of Mathematics,
Vol. 64,
Issue. 1,
Madady Moghadam, Safoura
and
Iranmanesh, Ali
2023.
Characterization of some almost simple groups with socle PSp4(q) by their character degrees.
Journal of Algebra and Its Applications,
Vol. 22,
Issue. 08,
Alavi, Seyed Hassan
2023.
On groups with the same character degrees as almost simple groups with socle small Ree groups.
Communications in Algebra,
Vol. 51,
Issue. 10,
p.
4372.
Alavi, Seyed Hassan
Daneshkhah, Ashraf
and
Zafarabad, Yazdan Momeni
2023.
Groups with the same character degrees as almost simple Suzuki groups.
Journal of Algebra and Its Applications,
Vol. 22,
Issue. 09,