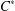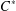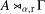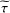Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
MENG, QING
2017.
HAAGERUP PROPERTY FOR -CROSSED PRODUCTS.
Bulletin of the Australian Mathematical Society,
Vol. 95,
Issue. 1,
p.
144.
MENG, QING
2018.
WEAK HAAGERUP PROPERTY OF-CROSSED PRODUCTS.
Bulletin of the Australian Mathematical Society,
Vol. 97,
Issue. 1,
p.
119.
MCKEE, ANDREW
SKALSKI, ADAM
TODOROV, IVAN G.
and
TUROWSKA, LYUDMILA
2018.
Positive Herz–Schur multipliers and approximation properties of crossed products.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 165,
Issue. 3,
p.
511.