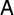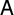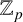1 Introduction
Let
![]() $p\neq 2$
be a fixed prime number. Let
$p\neq 2$
be a fixed prime number. Let
![]() $\mathsf {A}$
be a simple modular self-dual abelian variety over a totally real field F so that F is isomorphic to a subfield of
$\mathsf {A}$
be a simple modular self-dual abelian variety over a totally real field F so that F is isomorphic to a subfield of
![]() $\mathrm {End}(\mathsf {A})\otimes \mathbb {Q}$
, with
$\mathrm {End}(\mathsf {A})\otimes \mathbb {Q}$
, with
![]() $d=\dim (\mathsf {A})=[F:\mathbb {Q}]$
. In particular,
$d=\dim (\mathsf {A})=[F:\mathbb {Q}]$
. In particular,
![]() $\mathsf {A}$
is a simple quotient of the Jacobian of a Shimura curve over F, corresponding to a Hilbert modular form. Let
$\mathsf {A}$
is a simple quotient of the Jacobian of a Shimura curve over F, corresponding to a Hilbert modular form. Let
![]() $\sigma _{\mathsf {A}}$
denote the weight 2 and level
$\sigma _{\mathsf {A}}$
denote the weight 2 and level
![]() $\mathfrak {N}$
cuspidal automorphic representation attached to
$\mathfrak {N}$
cuspidal automorphic representation attached to
![]() $\mathsf {A}$
. Since
$\mathsf {A}$
. Since
![]() $\mathsf {A}$
is self-dual, the central character of
$\mathsf {A}$
is self-dual, the central character of
![]() $\sigma _{\mathsf {A}}$
is trivial.
$\sigma _{\mathsf {A}}$
is trivial.
Throughout, we assume the following hypothesis holds.
-
(ORD)
 $\mathsf {A}$
has potentially good ordinary reduction at all primes above p.
$\mathsf {A}$
has potentially good ordinary reduction at all primes above p.
Let K be a complex multiplication (CM) extension of F and suppose that the Leopoldt conjecture is satisfied, that is, the compositum of all
![]() $\mathbb {Z}_p$
-extensions of K, which we denote by
$\mathbb {Z}_p$
-extensions of K, which we denote by
![]() $K_\infty $
, is a
$K_\infty $
, is a
![]() $(d+1)$
-dimensional abelian p-adic Lie group. Let
$(d+1)$
-dimensional abelian p-adic Lie group. Let
![]() $\Gamma _\infty =\operatorname {Gal}(K_\infty /K)\cong \mathbb {Z}_p^{\oplus (d+1)}$
.
$\Gamma _\infty =\operatorname {Gal}(K_\infty /K)\cong \mathbb {Z}_p^{\oplus (d+1)}$
.
Let
![]() $\mathfrak {p}\mid p$
be a fixed prime of F, which induces an embedding
$\mathfrak {p}\mid p$
be a fixed prime of F, which induces an embedding
![]() $\iota _{\mathfrak {p}}:\overline {\mathbb {Q}}\hookrightarrow \overline {\mathbb {Q}_p}$
. The ring of integers of the completion
$\iota _{\mathfrak {p}}:\overline {\mathbb {Q}}\hookrightarrow \overline {\mathbb {Q}_p}$
. The ring of integers of the completion
![]() $F_{\mathfrak {p}}$
is denoted by
$F_{\mathfrak {p}}$
is denoted by
![]() $\mathcal {O}_{\mathfrak {p}}$
. We are interested in the growth of the
$\mathcal {O}_{\mathfrak {p}}$
. We are interested in the growth of the
![]() $\mathcal {O}_{\mathfrak {p}}$
-corank of
$\mathcal {O}_{\mathfrak {p}}$
-corank of
![]() $\mathfrak {p}$
-primary Selmer groups of
$\mathfrak {p}$
-primary Selmer groups of
![]() $\mathsf {A}$
over
$\mathsf {A}$
over
![]() $\mathbb {Z}_p$
-extensions of K. When
$\mathbb {Z}_p$
-extensions of K. When
![]() $F=\mathbb {Q}$
and
$F=\mathbb {Q}$
and
![]() $\mathsf {A}$
is an elliptic curve, it is predicted by Mazur [Reference Mazur, Ciesielski and Olech25, Section 18] that the Selmer coranks of
$\mathsf {A}$
is an elliptic curve, it is predicted by Mazur [Reference Mazur, Ciesielski and Olech25, Section 18] that the Selmer coranks of
![]() $\mathsf {A}$
over finite extensions of K inside a
$\mathsf {A}$
over finite extensions of K inside a
![]() $\mathbb {Z}_p$
-extension should be bounded, except possibly the anticyclotomic
$\mathbb {Z}_p$
-extension should be bounded, except possibly the anticyclotomic
![]() $\mathbb {Z}_p$
-extension when
$\mathbb {Z}_p$
-extension when
![]() $\mathsf {A}/K$
has root number
$\mathsf {A}/K$
has root number
![]() $-1$
. More generally, in [Reference Mazur, Rubin, Bloch, Fesenko, Illusie, Kurihara, Saito, Saito and Schneider26, Question 2.13], Mazur and Rubin asked whether it might be possible to use towers of Heegner points in Shimura curves over totally real fields to account for (at least some of) the expected Mordell–Weil growth as one ascends the finite intermediate extensions of the anti-cyclotomic hyperplane.
$-1$
. More generally, in [Reference Mazur, Rubin, Bloch, Fesenko, Illusie, Kurihara, Saito, Saito and Schneider26, Question 2.13], Mazur and Rubin asked whether it might be possible to use towers of Heegner points in Shimura curves over totally real fields to account for (at least some of) the expected Mordell–Weil growth as one ascends the finite intermediate extensions of the anti-cyclotomic hyperplane.
Our results are inspired by this question, the recent developments on the p-adic Gross–Zagier formula on Shimura curves by Disegni [Reference Disegni6] and the works of Neková
![]() $\breve{\rm r}$
[Reference Nekovář28, Reference Nekovář, Burns, Buzzard and Nekovář29], which show that growth in the anticyclotomic direction can indeed be accounted for by Heegner points. More precisely, we study the following analogue of Mazur’s growth number conjecture.
$\breve{\rm r}$
[Reference Nekovář28, Reference Nekovář, Burns, Buzzard and Nekovář29], which show that growth in the anticyclotomic direction can indeed be accounted for by Heegner points. More precisely, we study the following analogue of Mazur’s growth number conjecture.
Conjecture 1.1 (Growth number problem).
Fix a prime
![]() $p\neq 2$
. Let
$p\neq 2$
. Let
![]() $\mathsf {A}$
be a simple modular self-dual abelian variety over a totally real field F with potentially good ordinary reduction at
$\mathsf {A}$
be a simple modular self-dual abelian variety over a totally real field F with potentially good ordinary reduction at
![]() $\mathfrak {p}\mid p$
. Let
$\mathfrak {p}\mid p$
. Let
![]() $K/F$
be a CM extension and
$K/F$
be a CM extension and
![]() $\mathcal {K}/K$
be a
$\mathcal {K}/K$
be a
![]() $\mathbb {Z}_p$
-extension. Denote by
$\mathbb {Z}_p$
-extension. Denote by
![]() $\mathcal {K}_n$
the unique subfield of degree
$\mathcal {K}_n$
the unique subfield of degree
![]() $p^n$
of K in
$p^n$
of K in
![]() $\mathcal {K}$
. Then, for
$\mathcal {K}$
. Then, for
![]() $n \gg 0$
,
$n \gg 0$
,
where the growth number c is given by
 $$ \begin{align*} c = \begin{cases} 0 & \text{ if } \mathcal{K} \not\subseteq K_{{\mathrm{ac}}} \text{ or } (\mathsf{A},K) \text{ has `sign' } +1,\\1 & \text{ if } \mathcal{K} \subseteq K_{{\mathrm{ac}}}, (\mathsf{A},K) \text{ has `sign' } -1 \text{ and is `generic'},\\2 & \text{ if } \mathcal{K} \subseteq K_{{\mathrm{ac}}}, (\mathsf{A},K) \text{ has `sign' } -1 \text{ and is `exceptional'}. \end{cases} \end{align*} $$
$$ \begin{align*} c = \begin{cases} 0 & \text{ if } \mathcal{K} \not\subseteq K_{{\mathrm{ac}}} \text{ or } (\mathsf{A},K) \text{ has `sign' } +1,\\1 & \text{ if } \mathcal{K} \subseteq K_{{\mathrm{ac}}}, (\mathsf{A},K) \text{ has `sign' } -1 \text{ and is `generic'},\\2 & \text{ if } \mathcal{K} \subseteq K_{{\mathrm{ac}}}, (\mathsf{A},K) \text{ has `sign' } -1 \text{ and is `exceptional'}. \end{cases} \end{align*} $$
Here,
![]() $K_{{\mathrm {ac}}}$
denotes the compositum of all anticyclotomic
$K_{{\mathrm {ac}}}$
denotes the compositum of all anticyclotomic
![]() $\mathbb {Z}_p$
-extensions of K and
$\mathbb {Z}_p$
-extensions of K and
![]() $\operatorname {Gal}(K_{{\mathrm {ac}}}/K) \simeq \mathbb {Z}_p^{\oplus d}$
. The pair
$\operatorname {Gal}(K_{{\mathrm {ac}}}/K) \simeq \mathbb {Z}_p^{\oplus d}$
. The pair
![]() $(\mathsf {A}, K)$
is called ‘generic’ if
$(\mathsf {A}, K)$
is called ‘generic’ if
![]() $\mathsf {A}$
has no CM or the CM field of
$\mathsf {A}$
has no CM or the CM field of
![]() $\mathsf {A}$
is different from K. The pair
$\mathsf {A}$
is different from K. The pair
![]() $(\mathsf {A}, K)$
is called ‘exceptional’ if
$(\mathsf {A}, K)$
is called ‘exceptional’ if
![]() $\mathsf {A}$
has CM by (an order in) K. The sign of
$\mathsf {A}$
has CM by (an order in) K. The sign of
![]() $(\mathsf {A}, K)$
is defined analogous to [Reference Mazur, Ciesielski and Olech25, Section 6] to mean:
$(\mathsf {A}, K)$
is defined analogous to [Reference Mazur, Ciesielski and Olech25, Section 6] to mean:
-
• the sign of the functional equation of
 $L(\mathsf {A}/K, s)$
in the ‘generic’ case and
$L(\mathsf {A}/K, s)$
in the ‘generic’ case and -
• the sign of the functional equation of
 $L(\varphi , s)$
in the ‘exceptional’ case, where
$L(\varphi , s)$
in the ‘exceptional’ case, where
 $\varphi $
is the Hecke character of K satisfying
$\varphi $
is the Hecke character of K satisfying
 $L(\mathsf {A}/F, s) = L(\varphi , s)$
.
$L(\mathsf {A}/F, s) = L(\varphi , s)$
.
1.1 Progress towards this problem
To our knowledge, Conjecture 1.1 has been previously studied mainly in the case when
![]() $F=\mathbb {Q}$
and
$F=\mathbb {Q}$
and
![]() $\mathsf {A}$
is an elliptic curve. The original conjecture is completely settled for CM elliptic curves in the ‘exceptional case’ (see [Reference Greenberg, Conrad and Rubin9, Theorems 1.7 and 1.8]). In a recent preprint [Reference Li and Xu23], Li and Xu study the growth of Mordell–Weil ranks of CM abelian varieties associated with Hecke characters of infinite type
$\mathsf {A}$
is an elliptic curve. The original conjecture is completely settled for CM elliptic curves in the ‘exceptional case’ (see [Reference Greenberg, Conrad and Rubin9, Theorems 1.7 and 1.8]). In a recent preprint [Reference Li and Xu23], Li and Xu study the growth of Mordell–Weil ranks of CM abelian varieties associated with Hecke characters of infinite type
![]() $(1,0)$
over an imaginary quadratic field K along the anticyclotomic
$(1,0)$
over an imaginary quadratic field K along the anticyclotomic
![]() $\mathbb {Z}_p$
-extension of K.
$\mathbb {Z}_p$
-extension of K.
In the last few years, there has been increased interest in understanding the original conjecture of Mazur for non-CM elliptic curves (see [Reference Gajek-Leonard, Hatley, Kundu and Lei8, Reference Kleine, Matar and Sujatha18, Reference Kundu and Lei19]). Each takes a different approach to solve special cases of the problem, but somewhat surprisingly, a solution is provided only when the Mordell–Weil rank of the elliptic curve over K is at most 1. These results also focus on the case where p is a prime of good ordinary reduction, the setting in which Mazur first formulated his conjecture.
1.2 Main result I
Our first result gives an affirmative answer to Conjecture 1.1 under the generalised Heegner hypothesis:
-
(GHH+)
 $\epsilon _{K/F}(\mathfrak {N})=(-1)^{d-1}$
, where
$\epsilon _{K/F}(\mathfrak {N})=(-1)^{d-1}$
, where
 $\epsilon _{K/F}$
is the quadratic character attached to the extension
$\epsilon _{K/F}$
is the quadratic character attached to the extension
 $K/F$
. Furthermore, all primes of F lying above p split into two distinct primes in K.
$K/F$
. Furthermore, all primes of F lying above p split into two distinct primes in K.
The proof is analytic in nature, relying on Heegner points attached to
![]() $\mathsf {A}$
over K and their relations with the derivative of a multi-variable
$\mathsf {A}$
over K and their relations with the derivative of a multi-variable
![]() $\mathfrak {p}$
-adic L-function (see Section 3). We assume one inclusion of the Iwasawa main conjecture of
$\mathfrak {p}$
-adic L-function (see Section 3). We assume one inclusion of the Iwasawa main conjecture of
![]() $\mathsf {A}$
over
$\mathsf {A}$
over
![]() $K_\infty $
holds, which allows us to study the growth of the Selmer corank via the analytic
$K_\infty $
holds, which allows us to study the growth of the Selmer corank via the analytic
![]() $\mathfrak {p}$
-adic L-function. It generalises our previous result [Reference Kundu and Lei19, Theorem A] wherein we proved Mazur’s growth number conjecture in
$\mathfrak {p}$
-adic L-function. It generalises our previous result [Reference Kundu and Lei19, Theorem A] wherein we proved Mazur’s growth number conjecture in
![]() $\mathbb {Z}_p$
-extensions of an imaginary quadratic field K for non-CM elliptic curves
$\mathbb {Z}_p$
-extensions of an imaginary quadratic field K for non-CM elliptic curves
![]() $\mathsf {E}/\mathbb {Q}$
at primes
$\mathsf {E}/\mathbb {Q}$
at primes
![]() $p\geq 5$
of good ordinary reduction under (comparable) technical hypotheses.
$p\geq 5$
of good ordinary reduction under (comparable) technical hypotheses.
Theorem 1.2 (Theorems 5.3 and 5.4).
Fix a prime
![]() $p\neq 2$
. Let
$p\neq 2$
. Let
![]() $\mathsf {A}$
be a simple modular self-dual abelian variety of
$\mathsf {A}$
be a simple modular self-dual abelian variety of
![]() $\mathrm {GL}_2$
-type over a totally real field F with trivial central character satisfying hypothesis (ORD). Let
$\mathrm {GL}_2$
-type over a totally real field F with trivial central character satisfying hypothesis (ORD). Let
![]() $K/F$
be a CM extension such that
$K/F$
be a CM extension such that
![]() $\mathsf {A}(K)[\mathfrak {p}]$
is trivial and the
$\mathsf {A}(K)[\mathfrak {p}]$
is trivial and the
![]() $\mathfrak {p}$
-primary Selmer group
$\mathfrak {p}$
-primary Selmer group
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})$
is a co-torsion
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})$
is a co-torsion
![]() $\Lambda _{\mathrm {cyc}}$
-module. Suppose that hypothesis (GHH+
) and one inclusion of the Iwasawa main conjecture for
$\Lambda _{\mathrm {cyc}}$
-module. Suppose that hypothesis (GHH+
) and one inclusion of the Iwasawa main conjecture for
![]() $\mathsf {A}$
over
$\mathsf {A}$
over
![]() $K_\infty $
holds (see hypothesis (h-IMC) in Section 5.1). Denote by
$K_\infty $
holds (see hypothesis (h-IMC) in Section 5.1). Denote by
![]() $z_{\mathrm {Heeg}}$
the Heegner point of
$z_{\mathrm {Heeg}}$
the Heegner point of
![]() $\mathsf {A}$
over K. If the p-adic height
$\mathsf {A}$
over K. If the p-adic height
![]() $ \langle z_{\mathrm {Heeg}}, z_{\mathrm {Heeg}} \rangle _K$
is nonzero, then Conjecture 1.1 has a positive answer.
$ \langle z_{\mathrm {Heeg}}, z_{\mathrm {Heeg}} \rangle _K$
is nonzero, then Conjecture 1.1 has a positive answer.
1.3 Main result II
Our second result, where we study the growth of the Selmer corank using characteristic ideals, is purely algebraic. It generalises [Reference Gajek-Leonard, Hatley, Kundu and Lei8, Theorem A], where Mazur’s growth number conjecture for elliptic curves over
![]() $\mathbb {Z}_p$
-extensions of an imaginary quadratic field K is studied under a hypothesis on the structure of the Selmer group over the unique
$\mathbb {Z}_p$
-extensions of an imaginary quadratic field K is studied under a hypothesis on the structure of the Selmer group over the unique
![]() $\mathbb {Z}_p^{\oplus 2}$
-extension of K. In particular, we extend this result to the setting of abelian varieties. Although we follow a line of argument similar to that presented in [Reference Gajek-Leonard, Hatley, Kundu and Lei8], we give a (slight) simplification of the result and remove the nonanomalous hypothesis.
$\mathbb {Z}_p^{\oplus 2}$
-extension of K. In particular, we extend this result to the setting of abelian varieties. Although we follow a line of argument similar to that presented in [Reference Gajek-Leonard, Hatley, Kundu and Lei8], we give a (slight) simplification of the result and remove the nonanomalous hypothesis.
In what follows,
![]() $K_{\mathrm {cyc}}$
denotes the cyclotomic
$K_{\mathrm {cyc}}$
denotes the cyclotomic
![]() $\mathbb {Z}_p$
-extension of K with
$\mathbb {Z}_p$
-extension of K with
![]() $\Gamma _{\mathrm {cyc}}=\operatorname {Gal}(K_{\mathrm {cyc}}/K)$
. Let
$\Gamma _{\mathrm {cyc}}=\operatorname {Gal}(K_{\mathrm {cyc}}/K)$
. Let
![]() $\mathcal {O}_{\mathfrak {p}}$
denote the ring of integers of the completion of F at
$\mathcal {O}_{\mathfrak {p}}$
denote the ring of integers of the completion of F at
![]() $\mathfrak {p}$
and write
$\mathfrak {p}$
and write
![]() $\Lambda _\infty $
(respectively
$\Lambda _\infty $
(respectively
![]() $\Lambda _{\mathrm {cyc}}$
) for the Iwasawa algebra
$\Lambda _{\mathrm {cyc}}$
) for the Iwasawa algebra ![]() (respectively
(respectively ![]() ).
).
Theorem 1.3 (Theorems 6.1 and 6.2).
Fix a prime
![]() $p\neq 2$
. Let
$p\neq 2$
. Let
![]() $\mathsf {A}$
be a simple modular self-dual abelian variety of
$\mathsf {A}$
be a simple modular self-dual abelian variety of
![]() $\mathrm {GL}_2$
-type over a totally real field F with trivial central character satisfying hypothesis (ORD). Let
$\mathrm {GL}_2$
-type over a totally real field F with trivial central character satisfying hypothesis (ORD). Let
![]() $K/F$
be a CM extension such that
$K/F$
be a CM extension such that
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
is
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
is
![]() $\Lambda _{\mathrm {cyc}}$
-torsion. Suppose that one of the following conditions holds:
$\Lambda _{\mathrm {cyc}}$
-torsion. Suppose that one of the following conditions holds:
-
(i) the order of vanishing of
 $\mathrm {char}_{\Lambda _{\mathrm {cyc}}}\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
at the trivial character of
$\mathrm {char}_{\Lambda _{\mathrm {cyc}}}\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
at the trivial character of
 $\Gamma _{\mathrm {cyc}}$
is
$\Gamma _{\mathrm {cyc}}$
is
 $0$
;
$0$
; -
(ii) hypothesis (GHH+ ) holds, the order of vanishing of
 $\mathrm {char}_{\Lambda _{\mathrm {cyc}}}\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
at the trivial character of
$\mathrm {char}_{\Lambda _{\mathrm {cyc}}}\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
at the trivial character of
 $\Gamma _{\mathrm {cyc}}$
is
$\Gamma _{\mathrm {cyc}}$
is
 $1$
and
$1$
and
 $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
is a direct sum of cyclic
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
is a direct sum of cyclic
 $\Lambda _\infty $
-modules.
$\Lambda _\infty $
-modules.
Then, Conjecture 1.1 has a positive answer.
1.4 Organisation
In the preliminary Section 2, we introduce the notation that is used throughout the paper. We remind the reader of some definitions and fundamental results that are used several times in our arguments. In Section 3, we review Disegni’s result on the
![]() $\mathfrak {p}$
-adic L-function attached to
$\mathfrak {p}$
-adic L-function attached to
![]() $\mathsf {A}$
, and the relation between its derivative and Heegner points proven in [Reference Disegni7]. We carry out calculations on the specialisation of the
$\mathsf {A}$
, and the relation between its derivative and Heegner points proven in [Reference Disegni7]. We carry out calculations on the specialisation of the
![]() $\mathfrak {p}$
-adic L-function to a
$\mathfrak {p}$
-adic L-function to a
![]() $\mathbb {Z}_p$
-extension of K, reducing its nonvanishing to that of the
$\mathbb {Z}_p$
-extension of K, reducing its nonvanishing to that of the
![]() $\mathfrak {p}$
-adic height of
$\mathfrak {p}$
-adic height of
![]() $z_{\mathrm {Heeg}}$
, which is crucially used in the proof of Theorem 1.2. Another key ingredient of the proof is to show that
$z_{\mathrm {Heeg}}$
, which is crucially used in the proof of Theorem 1.2. Another key ingredient of the proof is to show that
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
admits no nontrivial pseudonull submodule; this is done in Section 4 using the main result of [Reference Greenberg, Loeffler and Zerbes13]. We complete the proof of the theorem in Section 5. In Section 6, we prove Theorem 1.3, providing evidence for Conjecture 1.1 using algebraic tools under a slightly different set of hypotheses.
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
admits no nontrivial pseudonull submodule; this is done in Section 4 using the main result of [Reference Greenberg, Loeffler and Zerbes13]. We complete the proof of the theorem in Section 5. In Section 6, we prove Theorem 1.3, providing evidence for Conjecture 1.1 using algebraic tools under a slightly different set of hypotheses.
1.5 Outlook
As has been pointed out previously, the higher rank case is still out of reach. The supersingular case would also require more work and new ideas. One may hope to use results on supersingular abelian varieties [Reference Büyükboduk and Lei3, Reference Büyükboduk and Lei4, Reference Isik and Lei17, Reference Lei and Ponsinet21, Reference Ponsinet32] combined with earlier works on elliptic curves [Reference Hung and Lim15, Reference Iovita and Pollack16, Reference Lei and Lim20, Reference Lei and Sprung22].
When the corank of
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)$
is one, our approach for studying Conjecture 1.1 hinges on the results of Disegni and Nekovár̆; therefore, the setup in which we can answer the question is dictated by their work. In particular, our method of proof cannot be used to address the question of Selmer rank growth in
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)$
is one, our approach for studying Conjecture 1.1 hinges on the results of Disegni and Nekovár̆; therefore, the setup in which we can answer the question is dictated by their work. In particular, our method of proof cannot be used to address the question of Selmer rank growth in
![]() $\mathbb {Z}_p$
-extensions of a general CM field K of an abelian variety
$\mathbb {Z}_p$
-extensions of a general CM field K of an abelian variety
![]() $\mathsf {A}$
that does not have real multiplication by the maximal real subfield of K. However, if
$\mathsf {A}$
that does not have real multiplication by the maximal real subfield of K. However, if
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)$
is finite, then standard arguments involving Mazur’s control theorem that we use to prove Theorem 1.3 under the condition (i) can be adapted readily to obtain an answer.
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)$
is finite, then standard arguments involving Mazur’s control theorem that we use to prove Theorem 1.3 under the condition (i) can be adapted readily to obtain an answer.
Let
![]() $\mathsf {A}$
be an abelian variety over a number field K and
$\mathsf {A}$
be an abelian variety over a number field K and
![]() $\mathcal {K}/K$
be a
$\mathcal {K}/K$
be a
![]() $\mathbb {Z}_p$
-extension. One can ask about the Selmer corank growth of
$\mathbb {Z}_p$
-extension. One can ask about the Selmer corank growth of
![]() $\mathrm {Sel}_{p^\infty }(\mathsf {A}/\mathcal {K}_n)$
as
$\mathrm {Sel}_{p^\infty }(\mathsf {A}/\mathcal {K}_n)$
as
![]() $n\to \infty $
, where
$n\to \infty $
, where
![]() $\mathcal {K}_n$
denotes the nth layer of
$\mathcal {K}_n$
denotes the nth layer of
![]() $\mathcal {K}/K$
. In the context of this paper, when K is a CM field and
$\mathcal {K}/K$
. In the context of this paper, when K is a CM field and
![]() $\mathsf {A}$
has real multiplication by the maximal real subfield of K, under appropriate hypotheses,
$\mathsf {A}$
has real multiplication by the maximal real subfield of K, under appropriate hypotheses,
 $$ \begin{align*} \mathrm{Sel}_{p^\infty}(\mathsf{A}/\mathcal{K}_n) = \bigoplus_{\mathfrak{p}\mid p} \mathrm{Sel}_{\mathfrak{p}^\infty}(\mathsf{A}/\mathcal{K}_n). \end{align*} $$
$$ \begin{align*} \mathrm{Sel}_{p^\infty}(\mathsf{A}/\mathcal{K}_n) = \bigoplus_{\mathfrak{p}\mid p} \mathrm{Sel}_{\mathfrak{p}^\infty}(\mathsf{A}/\mathcal{K}_n). \end{align*} $$
Thus,
![]() $ \mathrm {corank}_{\mathbb {Z}_p}\mathrm {Sel}_{p^\infty }(\mathsf {A}/\mathcal {K}_n) = cdp^n + O(1)$
, where c is the ‘growth number’ in Conjecture 1.1 and
$ \mathrm {corank}_{\mathbb {Z}_p}\mathrm {Sel}_{p^\infty }(\mathsf {A}/\mathcal {K}_n) = cdp^n + O(1)$
, where c is the ‘growth number’ in Conjecture 1.1 and
![]() $d=\dim (\mathsf {A})$
. One may speculate that such a formula might hold for more general number fields K.
$d=\dim (\mathsf {A})$
. One may speculate that such a formula might hold for more general number fields K.
2 Notation and preliminaries
2.1 Iwasawa algebras and projections
Recall from the introduction that F is a totally real field of degree d and K is a CM extension of F. The compositum of all
![]() $\mathbb {Z}_p$
-extensions of K is denoted by
$\mathbb {Z}_p$
-extensions of K is denoted by
![]() $K_\infty $
and
$K_\infty $
and
![]() $\Gamma _\infty =\operatorname {Gal}(K_\infty /K)\cong \mathbb {Z}_p^{\oplus (d+1)}$
. Let
$\Gamma _\infty =\operatorname {Gal}(K_\infty /K)\cong \mathbb {Z}_p^{\oplus (d+1)}$
. Let
![]() $K_{\mathrm {cyc}}$
be the cyclotomic
$K_{\mathrm {cyc}}$
be the cyclotomic
![]() $\mathbb {Z}_p$
-extension of K and
$\mathbb {Z}_p$
-extension of K and
![]() $K_{\mathrm {ac}}$
the anticyclotomic extension of K inside
$K_{\mathrm {ac}}$
the anticyclotomic extension of K inside
![]() $K_\infty $
. Write
$K_\infty $
. Write
where
![]() $\operatorname {Gal}(K_{\mathrm {cyc}}/K)$
is generated by
$\operatorname {Gal}(K_{\mathrm {cyc}}/K)$
is generated by
![]() $\sigma _0$
and
$\sigma _0$
and
![]() $\operatorname {Gal}(K_{\mathrm {ac}}/K)$
is generated by
$\operatorname {Gal}(K_{\mathrm {ac}}/K)$
is generated by
![]() $\sigma _1,\ldots ,\sigma _d$
. This gives rise to the isomorphism
$\sigma _1,\ldots ,\sigma _d$
. This gives rise to the isomorphism
sending
![]() $\sigma _i$
to
$\sigma _i$
to
![]() $X_i-1$
.
$X_i-1$
.
Given a
![]() $\mathbb {Z}_p$
-extension
$\mathbb {Z}_p$
-extension
![]() $\mathcal {K}/K$
with
$\mathcal {K}/K$
with
![]() $\Gamma _{\mathcal {K}}=\operatorname {Gal}(\mathcal {K}/K)$
, we have a natural projection
$\Gamma _{\mathcal {K}}=\operatorname {Gal}(\mathcal {K}/K)$
, we have a natural projection
whose kernel is isomorphic to
![]() $\mathbb {Z}_p^{\oplus d}$
. We can write
$\mathbb {Z}_p^{\oplus d}$
. We can write
 $$ \begin{align*} \ker\pi_{\mathcal{K}}=\bigg\{\kern-2pt\prod_{i=0}^d\sigma_i^{c_i}:\sum_{i=0}^da_ic_i=0\bigg\} \end{align*} $$
$$ \begin{align*} \ker\pi_{\mathcal{K}}=\bigg\{\kern-2pt\prod_{i=0}^d\sigma_i^{c_i}:\sum_{i=0}^da_ic_i=0\bigg\} \end{align*} $$
for some
![]() $a_i\in \mathbb {Z}_p$
not all zero. This allows us to identify the set of
$a_i\in \mathbb {Z}_p$
not all zero. This allows us to identify the set of
![]() $\mathbb {Z}_p$
-extensions of K with
$\mathbb {Z}_p$
-extensions of K with
![]() $\mathbb {P}^d(\mathbb {Z}_p)$
. After scaling if necessary, we may assume that
$\mathbb {P}^d(\mathbb {Z}_p)$
. After scaling if necessary, we may assume that
![]() $c_j\in \mathbb {Z}_p^\times $
for some
$c_j\in \mathbb {Z}_p^\times $
for some
![]() $j=j(\mathcal {K})$
. Then, for all
$j=j(\mathcal {K})$
. Then, for all
![]() $i\in \{0,\ldots ,d\}$
,
$i\in \{0,\ldots ,d\}$
,
In particular, we see that
![]() $\Gamma _{\mathcal {K}}$
is topologically generated by
$\Gamma _{\mathcal {K}}$
is topologically generated by
![]() $\pi _{\mathcal {K}}(\sigma _{j(\mathcal {K})})$
. We shall denote this element by
$\pi _{\mathcal {K}}(\sigma _{j(\mathcal {K})})$
. We shall denote this element by
![]() $\sigma _{\mathcal {K}}$
and write
$\sigma _{\mathcal {K}}$
and write
![]() $X_{\mathcal {K}}=\sigma _{\mathcal {K}}-1$
.
$X_{\mathcal {K}}=\sigma _{\mathcal {K}}-1$
.
Set ![]() . The natural extension of
. The natural extension of
![]() $\pi _{\mathcal {K}}$
to
$\pi _{\mathcal {K}}$
to
![]() $\Lambda _\infty \rightarrow \Lambda _{\mathcal {K}}$
(which we still denote by the same symbol) can be realised as
$\Lambda _\infty \rightarrow \Lambda _{\mathcal {K}}$
(which we still denote by the same symbol) can be realised as

Therefore,
 $$ \begin{align*} \frac{d\pi_K(f)}{d X_{\mathcal{K}}}=\sum_{i=0}^d \frac{c_i}{c_{j(\mathcal{K})}}(1+X_{\mathcal{K}})^{{c_i}/{c_{j(\mathcal{K})}}-1}\frac{\partial f}{\partial X_i}((1+X_{\mathcal{K}})^{{c_0}/{c_{j(\mathcal{K})}}}-1,\ldots,(1+X_{\mathcal{K}})^{{c_d}/{c_{j(\mathcal{K})}}}-1), \end{align*} $$
$$ \begin{align*} \frac{d\pi_K(f)}{d X_{\mathcal{K}}}=\sum_{i=0}^d \frac{c_i}{c_{j(\mathcal{K})}}(1+X_{\mathcal{K}})^{{c_i}/{c_{j(\mathcal{K})}}-1}\frac{\partial f}{\partial X_i}((1+X_{\mathcal{K}})^{{c_0}/{c_{j(\mathcal{K})}}}-1,\ldots,(1+X_{\mathcal{K}})^{{c_d}/{c_{j(\mathcal{K})}}}-1), \end{align*} $$
which tells us that
 $$ \begin{align} \frac{d\pi_K(f)}{d X_{\mathcal{K}}}\bigg|_{X_{\mathcal{K}}=0}=\sum_{i=0}^d \frac{c_i}{c_{j(\mathcal{K})}}\cdot\frac{\partial f}{\partial X_i}(0,\ldots,0). \end{align} $$
$$ \begin{align} \frac{d\pi_K(f)}{d X_{\mathcal{K}}}\bigg|_{X_{\mathcal{K}}=0}=\sum_{i=0}^d \frac{c_i}{c_{j(\mathcal{K})}}\cdot\frac{\partial f}{\partial X_i}(0,\ldots,0). \end{align} $$
Note that if
![]() $\mathcal {K}=K_{\mathrm {cyc}}$
, then
$\mathcal {K}=K_{\mathrm {cyc}}$
, then
![]() $j(K_{\mathrm {cyc}})=0$
, corresponding to
$j(K_{\mathrm {cyc}})=0$
, corresponding to
![]() $(1:0:\cdots :0)\in \mathbb {P}^d(\mathbb {Z}_p)$
. We write
$(1:0:\cdots :0)\in \mathbb {P}^d(\mathbb {Z}_p)$
. We write
![]() $\pi _{\mathrm {cyc}}$
for
$\pi _{\mathrm {cyc}}$
for
![]() $\pi _{K_{\mathrm {cyc}}}$
, which is given by
$\pi _{K_{\mathrm {cyc}}}$
, which is given by
![]() $f(X_0,X_1,\ldots ,X_d)\mapsto f(X_0,0,\ldots ,0)$
. Furthermore, we write
$f(X_0,X_1,\ldots ,X_d)\mapsto f(X_0,0,\ldots ,0)$
. Furthermore, we write ![]() for the corresponding Iwasawa algebra.
for the corresponding Iwasawa algebra.
Throughout, we often consider
![]() $\mathcal {K}$
to be a nonanticyclotomic
$\mathcal {K}$
to be a nonanticyclotomic
![]() $\mathbb {Z}_p$
-extension of K, that is,
$\mathbb {Z}_p$
-extension of K, that is,
![]() $\mathcal {K}\not \subseteq K_{{\mathrm {ac}}}$
. Such
$\mathcal {K}\not \subseteq K_{{\mathrm {ac}}}$
. Such
![]() $\mathcal {K}$
correspond to
$\mathcal {K}$
correspond to
![]() $(c_0:\cdots :c_d)\in \mathbb {P}^d(\mathbb {Z}_p)$
, where
$(c_0:\cdots :c_d)\in \mathbb {P}^d(\mathbb {Z}_p)$
, where
![]() $c_0\ne 0$
.
$c_0\ne 0$
.
2.2 Control theorems and rank growth in
 $\mathbb {Z}_{p}$
-extensions of number fields
$\mathbb {Z}_{p}$
-extensions of number fields
Let
![]() $\mathsf {A}/F$
be a simple abelian variety of
$\mathsf {A}/F$
be a simple abelian variety of
![]() $\mathrm {GL}_2$
-type and level
$\mathrm {GL}_2$
-type and level
![]() $\mathfrak {N}$
over a totally real field F with potentially good ordinary reduction at all primes above p. Let
$\mathfrak {N}$
over a totally real field F with potentially good ordinary reduction at all primes above p. Let
![]() $\Sigma (F)$
be a finite set of primes in F containing
$\Sigma (F)$
be a finite set of primes in F containing
![]() $\mathfrak {p}$
and all primes of bad reduction for
$\mathfrak {p}$
and all primes of bad reduction for
![]() $\mathsf {A}$
; in other words,
$\mathsf {A}$
; in other words,
![]() $\Sigma (F) \supseteq \{\mathfrak {p} \} \cup \{v \colon v \mid \mathfrak {N}\}$
. For any field
$\Sigma (F) \supseteq \{\mathfrak {p} \} \cup \{v \colon v \mid \mathfrak {N}\}$
. For any field
![]() $L/F$
, define
$L/F$
, define
![]() $\Sigma (L)$
to be the set of places of L lying above those in
$\Sigma (L)$
to be the set of places of L lying above those in
![]() $\Sigma (F)$
and write
$\Sigma (F)$
and write
![]() $G_\Sigma (L)$
for the Galois group of the maximal extension of L that is unramified outside of
$G_\Sigma (L)$
for the Galois group of the maximal extension of L that is unramified outside of
![]() $\Sigma (L)$
. For any
$\Sigma (L)$
. For any
![]() $v \in \Sigma (F)$
and any finite extension
$v \in \Sigma (F)$
and any finite extension
![]() $L/F$
, write
$L/F$
, write
 $$ \begin{align*} J_v(\mathsf{A}/L)= \bigoplus_{w\mid v} H^1(L_w,\mathsf{A})[\mathfrak{p}^\infty]. \end{align*} $$
$$ \begin{align*} J_v(\mathsf{A}/L)= \bigoplus_{w\mid v} H^1(L_w,\mathsf{A})[\mathfrak{p}^\infty]. \end{align*} $$
When
![]() $\mathcal {L}/L$
is an infinite extension of L, set
$\mathcal {L}/L$
is an infinite extension of L, set
Definition 2.1. Let
![]() $\mathsf {A}/F$
be a simple abelian variety of
$\mathsf {A}/F$
be a simple abelian variety of
![]() $\mathrm {GL}_2$
-type over a totally real field F with potentially good ordinary reduction at all primes above p. Let
$\mathrm {GL}_2$
-type over a totally real field F with potentially good ordinary reduction at all primes above p. Let
![]() $\Sigma (F)$
be any finite set of primes containing those dividing
$\Sigma (F)$
be any finite set of primes containing those dividing
![]() $\mathfrak {p}\mathfrak {N}$
. For any extension
$\mathfrak {p}\mathfrak {N}$
. For any extension
![]() $L/F$
, define the Selmer group
$L/F$
, define the Selmer group
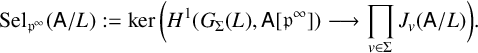 $$ \begin{align*} \mathrm{Sel}_{\mathfrak{p}^\infty}(\mathsf{A}/L):=\ker \bigg( H^1(G_{\Sigma}(L),\mathsf{A}[\mathfrak{p}^\infty]) \longrightarrow \prod_{v \in \Sigma} J_v(\mathsf{A}/L) \bigg). \end{align*} $$
$$ \begin{align*} \mathrm{Sel}_{\mathfrak{p}^\infty}(\mathsf{A}/L):=\ker \bigg( H^1(G_{\Sigma}(L),\mathsf{A}[\mathfrak{p}^\infty]) \longrightarrow \prod_{v \in \Sigma} J_v(\mathsf{A}/L) \bigg). \end{align*} $$
We now recall the statement of Mazur’s control theorem, which allows us to study the growth behaviour of Selmer groups in
![]() $\mathbb {Z}_p$
-extensions.
$\mathbb {Z}_p$
-extensions.
Theorem 2.2 (Mazur’s control theorem).
Fix an odd prime p. Let F be a totally real number field and let
![]() $\mathsf {A}/F$
be an abelian variety of
$\mathsf {A}/F$
be an abelian variety of
![]() $\mathrm {GL}_2$
-type which has potentially ordinary reduction at all primes of F lying over p. Let
$\mathrm {GL}_2$
-type which has potentially ordinary reduction at all primes of F lying over p. Let
![]() $K/F$
be a quadratic extension of F which is a CM field. Let
$K/F$
be a quadratic extension of F which is a CM field. Let
![]() $\mathcal {K}$
be any
$\mathcal {K}$
be any
![]() $\mathbb {Z}_p$
-extension of K and
$\mathbb {Z}_p$
-extension of K and
![]() $\mathcal {K}_n$
denote the nth layer of this extension with
$\mathcal {K}_n$
denote the nth layer of this extension with
![]() $\operatorname {Gal}(\mathcal {K}_n/K) \simeq \mathbb {Z}/p^n\mathbb {Z}$
. Then, the kernel and cokernel of the natural map
$\operatorname {Gal}(\mathcal {K}_n/K) \simeq \mathbb {Z}/p^n\mathbb {Z}$
. Then, the kernel and cokernel of the natural map
are finite and of bounded order independent of n.
Proof. This is proved in the same way as [Reference Greenberg10, Proposition 5.1]; see also [Reference Murty and Ouyang27, Theorem 2].
Corollary 2.3. With the assumptions of Theorem 2.2, set
![]() $r {\kern-1pt}={\kern-1pt} \mathrm {corank}_{\Lambda _{\mathcal {K}}}(\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K}))$
. Then, as
$r {\kern-1pt}={\kern-1pt} \mathrm {corank}_{\Lambda _{\mathcal {K}}}(\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K}))$
. Then, as
![]() $n\to \infty $
,
$n\to \infty $
,
In particular, if
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)$
is finite, then as
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)$
is finite, then as
![]() $n\to \infty $
,
$n\to \infty $
,
Proof. The arguments for both assertions are standard. They are recorded in [Reference Greenberg, Conrad and Rubin9, Corollaries 4.9 and 4.12] for
![]() $\mathbb {Z}_p$
-coranks of
$\mathbb {Z}_p$
-coranks of
![]() $p^\infty $
-Selmer groups of elliptic curves, but the proofs go through for the current setting.
$p^\infty $
-Selmer groups of elliptic curves, but the proofs go through for the current setting.
3
 $\mathfrak {p}$
-adic L-functions
$\mathfrak {p}$
-adic L-functions
Throughout this section, we assume hypothesis (GHH+ ) holds. We review results of Disegni [Reference Disegni6] that will be used in our proof of Theorem 1.2. For each place of F lying above p, we fix a level 0 additive character (see [Reference Disegni6, end of page 1993]).
Theorem 3.1 [Reference Disegni6, Theorem A].
Let
![]() $\mathfrak {p}$
be a place of F lying above p where
$\mathfrak {p}$
be a place of F lying above p where
![]() $\mathsf {A}$
has potentially good ordinary reduction. There exists a unique
$\mathsf {A}$
has potentially good ordinary reduction. There exists a unique
![]() $\mathfrak {p}$
-adic L-function
$\mathfrak {p}$
-adic L-function
![]() ${L_{\mathfrak {p}}(\mathsf {A})\in F_{\mathfrak {p}}\otimes \Lambda _\infty }$
such that for all finite characters
${L_{\mathfrak {p}}(\mathsf {A})\in F_{\mathfrak {p}}\otimes \Lambda _\infty }$
such that for all finite characters
![]() $\chi $
of
$\chi $
of
![]() $\Gamma _\infty $
,
$\Gamma _\infty $
,
for some constant
![]() $C_\chi $
and a period
$C_\chi $
and a period
![]() $\Omega $
.
$\Omega $
.
Here,
![]() ${L(\mathsf {A}/K,\chi ,1)}/{\Omega }$
is an algebraic number, regarded as an element of
${L(\mathsf {A}/K,\chi ,1)}/{\Omega }$
is an algebraic number, regarded as an element of
![]() $\overline {\mathbb {Q}_p}$
through
$\overline {\mathbb {Q}_p}$
through
![]() $\iota _{\mathfrak {p}}$
. Many authors, including [Reference Disegni6], refer to
$\iota _{\mathfrak {p}}$
. Many authors, including [Reference Disegni6], refer to
![]() $L_{\mathfrak {p}}$
as a p-adic L-function, but to highlight the dependence on
$L_{\mathfrak {p}}$
as a p-adic L-function, but to highlight the dependence on
![]() $\mathfrak {p}\mid p$
, we refer to it as a
$\mathfrak {p}\mid p$
, we refer to it as a
![]() $\mathfrak {p}$
-adic L-function.
$\mathfrak {p}$
-adic L-function.
The sign of the functional equation of
![]() $L(\mathsf {A},K,\chi ,s)$
at
$L(\mathsf {A},K,\chi ,s)$
at
![]() $s=1$
is constant for all finite characters
$s=1$
is constant for all finite characters
![]() $\chi $
of
$\chi $
of
![]() $\operatorname {Gal}(K_{\mathrm {ac}}/K)$
(see [Reference Disegni6, top of page 1999]). In particular, since
$\operatorname {Gal}(K_{\mathrm {ac}}/K)$
(see [Reference Disegni6, top of page 1999]). In particular, since
![]() $\mathsf {A}$
is assumed to be self-dual,
$\mathsf {A}$
is assumed to be self-dual,
![]() $L_{\mathfrak {p}}(\mathsf {A})(\chi )=0$
for all such
$L_{\mathfrak {p}}(\mathsf {A})(\chi )=0$
for all such
![]() $\chi $
under our running hypotheses. If we consider
$\chi $
under our running hypotheses. If we consider
![]() $L_{\mathfrak {p}}(\mathsf {A})$
as a power series in
$L_{\mathfrak {p}}(\mathsf {A})$
as a power series in
![]() $X_0,X_1,\ldots , X_d$
, we have
$X_0,X_1,\ldots , X_d$
, we have
![]() $L_{\mathfrak {p}}(\mathsf {A})(0,X_1,\ldots ,X_d)=0$
. Consequently, we can expand
$L_{\mathfrak {p}}(\mathsf {A})(0,X_1,\ldots ,X_d)=0$
. Consequently, we can expand
![]() $L_{\mathfrak {p}}(\mathsf {A})$
as a power series in
$L_{\mathfrak {p}}(\mathsf {A})$
as a power series in
![]() $X_0$
with coefficients in
$X_0$
with coefficients in
![]() $\Lambda _{\mathrm {ac}}\bigotimes _{\mathbb {Z}_p}\mathbb {Q}_p$
, where
$\Lambda _{\mathrm {ac}}\bigotimes _{\mathbb {Z}_p}\mathbb {Q}_p$
, where ![]() . More specifically,
. More specifically,
where
![]() $G_{\mathfrak {p}}(A)\in \Lambda _{\mathrm {ac}}\otimes \mathbb {Q}_p$
.
$G_{\mathfrak {p}}(A)\in \Lambda _{\mathrm {ac}}\otimes \mathbb {Q}_p$
.
Proposition 3.2. Let
![]() $\mathcal {K}$
be a nonanticyclotomic
$\mathcal {K}$
be a nonanticyclotomic
![]() $\mathbb {Z}_p$
-extension of K. If
$\mathbb {Z}_p$
-extension of K. If
![]() $G_{\mathfrak {p}}(\mathsf {A}) (0,\ldots ,0)\ne 0$
, then
$G_{\mathfrak {p}}(\mathsf {A}) (0,\ldots ,0)\ne 0$
, then
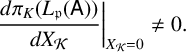 $$ \begin{align*} \frac{d\pi_K(L_{\mathfrak{p}}(\mathsf{A}))}{d X_{\mathcal{K}}}\bigg|_{X_{\mathcal{K}}=0}\ne0. \end{align*} $$
$$ \begin{align*} \frac{d\pi_K(L_{\mathfrak{p}}(\mathsf{A}))}{d X_{\mathcal{K}}}\bigg|_{X_{\mathcal{K}}=0}\ne0. \end{align*} $$
Proof. Recall that
![]() $\mathcal {K}$
corresponds to a
$\mathcal {K}$
corresponds to a
![]() $\mathbb {Z}_p$
-extension such that
$\mathbb {Z}_p$
-extension such that
![]() $(c_0:\cdots :c_d)\in \mathbb {P}^d(\mathbb {Z}_p)$
with
$(c_0:\cdots :c_d)\in \mathbb {P}^d(\mathbb {Z}_p)$
with
![]() $c_0\ne 0$
. It follows from (2.1) and (3.1) that
$c_0\ne 0$
. It follows from (2.1) and (3.1) that
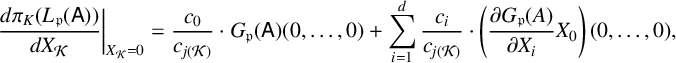 $$ \begin{align*} \frac{d\pi_K(L_{\mathfrak{p}}(\mathsf{A}))}{d X_{\mathcal{K}}}\bigg|_{X_{\mathcal{K}}=0}=\frac{c_0}{c_{j(\mathcal{K})}}\cdot G_{\mathfrak{p}}(\mathsf{A})(0,\ldots,0)+\sum_{i=1}^d\frac{c_i}{c_{j(\mathcal{K})}}\cdot\left(\frac{\partial G_{\mathfrak{p}}(A)}{\partial X_i}X_0\right)(0,\ldots,0), \end{align*} $$
$$ \begin{align*} \frac{d\pi_K(L_{\mathfrak{p}}(\mathsf{A}))}{d X_{\mathcal{K}}}\bigg|_{X_{\mathcal{K}}=0}=\frac{c_0}{c_{j(\mathcal{K})}}\cdot G_{\mathfrak{p}}(\mathsf{A})(0,\ldots,0)+\sum_{i=1}^d\frac{c_i}{c_{j(\mathcal{K})}}\cdot\left(\frac{\partial G_{\mathfrak{p}}(A)}{\partial X_i}X_0\right)(0,\ldots,0), \end{align*} $$
which is a nonzero multiple of
![]() $G_{\mathfrak {p}}(\mathsf {A})(0,\ldots ,0)$
. Hence, the lemma follows.
$G_{\mathfrak {p}}(\mathsf {A})(0,\ldots ,0)$
. Hence, the lemma follows.
By [Reference Disegni6, Theorem C(4)],
![]() $G_{\mathfrak {p}}(\mathsf {A})$
is described via the
$G_{\mathfrak {p}}(\mathsf {A})$
is described via the
![]() $\Lambda _{\mathrm {ac}}$
-adic heights of the Heegner points on
$\Lambda _{\mathrm {ac}}$
-adic heights of the Heegner points on
![]() $\mathsf {A}$
defined over finite sub-extensions of
$\mathsf {A}$
defined over finite sub-extensions of
![]() $K_{\mathrm {ac}}/K$
. In particular,
$K_{\mathrm {ac}}/K$
. In particular,
![]() $G_{\mathfrak {p}}(\mathsf {A})(0,\ldots ,0)$
is a nonzero multiple of the
$G_{\mathfrak {p}}(\mathsf {A})(0,\ldots ,0)$
is a nonzero multiple of the
![]() $\mathfrak {p}$
-adic height of the Heegner point
$\mathfrak {p}$
-adic height of the Heegner point
![]() $z_{\mathrm {Heeg}}$
attached to
$z_{\mathrm {Heeg}}$
attached to
![]() $\mathsf {A}/K$
. The reader is referred to [Reference Disegni6, Section 1.1] for the definition of
$\mathsf {A}/K$
. The reader is referred to [Reference Disegni6, Section 1.1] for the definition of
![]() $z_{\mathrm {Heeg}}$
(where the character
$z_{\mathrm {Heeg}}$
(where the character
![]() $\chi $
in [Reference Disegni6] is taken to be the trivial character).
$\chi $
in [Reference Disegni6] is taken to be the trivial character).
We use the notation
![]() $\langle -,-\rangle _K$
to denote the p-adic height associated with
$\langle -,-\rangle _K$
to denote the p-adic height associated with
![]() $\mathfrak {p}$
over K, as given in [Reference Disegni7, Section 1.3]. We consider the hypothesis:
$\mathfrak {p}$
over K, as given in [Reference Disegni7, Section 1.3]. We consider the hypothesis:
-
(HGT)
 $\langle z_{\mathrm {Heeg}},z_{\mathrm {Heeg}}\rangle _K\ne 0$
.
$\langle z_{\mathrm {Heeg}},z_{\mathrm {Heeg}}\rangle _K\ne 0$
.
From Proposition 3.2, we can deduce the following result.
Corollary 3.3. Let
![]() $\mathcal {K}$
be a nonanticyclotomic
$\mathcal {K}$
be a nonanticyclotomic
![]() $\mathbb {Z}_p$
-extension of K. If hypothesis (HGT) holds, then
$\mathbb {Z}_p$
-extension of K. If hypothesis (HGT) holds, then
 $$ \begin{align*} \frac{d\pi_K(L_{\mathfrak{p}}(\mathsf{A}))}{d X_{\mathcal{K}}}\bigg|_{X_{\mathcal{K}}=0}\ne0. \end{align*} $$
$$ \begin{align*} \frac{d\pi_K(L_{\mathfrak{p}}(\mathsf{A}))}{d X_{\mathcal{K}}}\bigg|_{X_{\mathcal{K}}=0}\ne0. \end{align*} $$
In particular,
![]() $\pi _{\mathcal {K}}(L_{\mathfrak {p}}(\mathsf {A}))\ne 0$
.
$\pi _{\mathcal {K}}(L_{\mathfrak {p}}(\mathsf {A}))\ne 0$
.
4 Nonexistence of nontrivial pseudonull submodules
In this section, we review a special case of a result of Greenberg [Reference Greenberg, Loeffler and Zerbes13, Proposition 4.1.1] regarding sufficient conditions for
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
to admit no nontrivial pseudonull submodule.
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
to admit no nontrivial pseudonull submodule.
Throughout this section, we keep the notation introduced previously. We further assume:
-
(CYC)
 $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
is
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
is
 $\Lambda _{\mathrm {cyc}}$
-torsion.
$\Lambda _{\mathrm {cyc}}$
-torsion.
In view of [Reference Hachimori and Ochiai14, Lemma 2.6] (which is based on the ideas in [Reference Balister and Howson1]), we can conclude that hypothesis (CYC) implies that
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
is
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
is
![]() $\Lambda _\infty $
-torsion.
$\Lambda _\infty $
-torsion.
Let
![]() $\mathcal {T}=T_{\mathfrak {p}}(\mathsf {A})\otimes \Lambda _\infty ^\iota $
, where
$\mathcal {T}=T_{\mathfrak {p}}(\mathsf {A})\otimes \Lambda _\infty ^\iota $
, where
![]() $\iota $
is the involution on
$\iota $
is the involution on
![]() $\Lambda _\infty $
sending a group-like element to its inverse, and set
$\Lambda _\infty $
sending a group-like element to its inverse, and set
![]() $\mathcal {D}=\mathcal {T}\bigotimes _{\Lambda _\infty } \Lambda _\infty ^\vee $
. Throughout this section, we will be consistent with the notation of [Reference Greenberg, Loeffler and Zerbes13, Section 2.1] as much as possible.
$\mathcal {D}=\mathcal {T}\bigotimes _{\Lambda _\infty } \Lambda _\infty ^\vee $
. Throughout this section, we will be consistent with the notation of [Reference Greenberg, Loeffler and Zerbes13, Section 2.1] as much as possible.
The condition RFX(
![]() $\mathcal {D}$
) asserts that
$\mathcal {D}$
) asserts that
![]() $\mathcal {T}$
is a reflexive
$\mathcal {T}$
is a reflexive
![]() $\Lambda _\infty $
-module; in our setting, this condition holds since
$\Lambda _\infty $
-module; in our setting, this condition holds since
![]() $\mathcal {T}$
is free over
$\mathcal {T}$
is free over
![]() $\Lambda _\infty $
. In our context, the condition LEO(
$\Lambda _\infty $
. In our context, the condition LEO(
![]() $\mathcal {D}$
) asserts that
$\mathcal {D}$
) asserts that
 $$ \begin{align*} \ker\bigg(H^2(K_\Sigma/K,\mathcal{D})\longrightarrow \prod_{v\in \Sigma}H^2(K_v,\mathcal{D})\bigg) \end{align*} $$
$$ \begin{align*} \ker\bigg(H^2(K_\Sigma/K,\mathcal{D})\longrightarrow \prod_{v\in \Sigma}H^2(K_v,\mathcal{D})\bigg) \end{align*} $$
is a cotorsion
![]() $\Lambda (G_K)$
-module. From [Reference Greenberg11, Theorem 3], there is an isomorphism of
$\Lambda (G_K)$
-module. From [Reference Greenberg11, Theorem 3], there is an isomorphism of
![]() $\Lambda (G_K)$
-modules
$\Lambda (G_K)$
-modules
![]() $H^2(K_\Sigma /K,\mathcal {D})\cong H^2(K_\Sigma /K_\infty , \mathsf {A}[\mathfrak {p}^\infty ])$
.
$H^2(K_\Sigma /K,\mathcal {D})\cong H^2(K_\Sigma /K_\infty , \mathsf {A}[\mathfrak {p}^\infty ])$
.
Since our hypotheses imply that
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
is
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
is
![]() $\Lambda _\infty $
-torsion, by arguments analogous to [Reference Ochi and Venjakob31, Theorem 3.2],
$\Lambda _\infty $
-torsion, by arguments analogous to [Reference Ochi and Venjakob31, Theorem 3.2],
where r is the
![]() $\mathcal {O}_{\mathfrak {p}}$
-corank of
$\mathcal {O}_{\mathfrak {p}}$
-corank of
![]() $\mathsf {A}[\mathfrak {p}^\infty ]$
. By combining [Reference Coates and Greenberg5, Proposition 4.8] and [Reference Ochi and Venjakob31, Theorem 4.1],
$\mathsf {A}[\mathfrak {p}^\infty ]$
. By combining [Reference Coates and Greenberg5, Proposition 4.8] and [Reference Ochi and Venjakob31, Theorem 4.1],
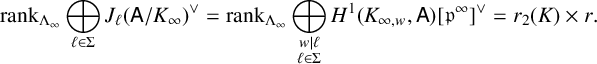 $$ \begin{align} \mathrm{rank}_{\Lambda_\infty}\bigoplus_{\ell\in \Sigma}J_\ell(\mathsf{A} /K_\infty)^\vee = \mathrm{rank}_{\Lambda_\infty}\bigoplus_{\substack{w\mid \ell \\ \ell\in \Sigma}} H^1(K_{\infty,w}, \mathsf{A})[\mathfrak{p}^{\infty}]^\vee = r_2(K) \times r. \end{align} $$
$$ \begin{align} \mathrm{rank}_{\Lambda_\infty}\bigoplus_{\ell\in \Sigma}J_\ell(\mathsf{A} /K_\infty)^\vee = \mathrm{rank}_{\Lambda_\infty}\bigoplus_{\substack{w\mid \ell \\ \ell\in \Sigma}} H^1(K_{\infty,w}, \mathsf{A})[\mathfrak{p}^{\infty}]^\vee = r_2(K) \times r. \end{align} $$
A standard argument with the Poitou–Tate exact sequence implies that the module
![]() $H^2(K_S/K_\infty , \mathsf {A}[\mathfrak {p}^\infty ])$
is co-torsion over
$H^2(K_S/K_\infty , \mathsf {A}[\mathfrak {p}^\infty ])$
is co-torsion over
![]() $\Lambda _\infty $
and the module
$\Lambda _\infty $
and the module
![]() $H^1(K_S/K_\infty , \mathsf {A}[\mathfrak {p}^\infty ])$
is of corank
$H^1(K_S/K_\infty , \mathsf {A}[\mathfrak {p}^\infty ])$
is of corank
![]() $r_2(K) \times r$
. In particular, condition LEO(
$r_2(K) \times r$
. In particular, condition LEO(
![]() $\mathcal {D}$
) holds.
$\mathcal {D}$
) holds.
The condition CRK
![]() $(\mathcal {D},\mathcal {L})$
asserts that
$(\mathcal {D},\mathcal {L})$
asserts that
 $$ \begin{align*} \mathrm{corank}_{\Lambda_\infty} H^1(K_\Sigma/K_\infty,\mathsf{A}[\mathfrak{p}^\infty]) & =\mathrm{corank}_{\Lambda_\infty} \mathrm{Sel}_{\mathfrak{p}^\infty}(\mathsf{A}/K_\infty)+\mathrm{corank}_{\Lambda_\infty}\bigoplus_{\ell\in \Sigma}J_\ell(\mathsf{A}/K_\infty) \\ & = \mathrm{corank}_{\Lambda_\infty}\bigoplus_{\ell\in \Sigma}J_\ell(\mathsf{A}/K_\infty) \end{align*} $$
$$ \begin{align*} \mathrm{corank}_{\Lambda_\infty} H^1(K_\Sigma/K_\infty,\mathsf{A}[\mathfrak{p}^\infty]) & =\mathrm{corank}_{\Lambda_\infty} \mathrm{Sel}_{\mathfrak{p}^\infty}(\mathsf{A}/K_\infty)+\mathrm{corank}_{\Lambda_\infty}\bigoplus_{\ell\in \Sigma}J_\ell(\mathsf{A}/K_\infty) \\ & = \mathrm{corank}_{\Lambda_\infty}\bigoplus_{\ell\in \Sigma}J_\ell(\mathsf{A}/K_\infty) \end{align*} $$
since we use hypothesis (CYC). The desired equality follows from (4.1) and (4.2).
We now consider the conditions LOC
![]() $_v^{(i)}(\mathcal {D})$
,
$_v^{(i)}(\mathcal {D})$
,
![]() $i=1,2$
. Write
$i=1,2$
. Write
![]() $\mathcal {T}^*=\mathrm {Hom}(\mathcal {D},\mu _{p^\infty })$
. The conditions assert that for
$\mathcal {T}^*=\mathrm {Hom}(\mathcal {D},\mu _{p^\infty })$
. The conditions assert that for
![]() $v\in \Sigma (K)$
, we have
$v\in \Sigma (K)$
, we have
![]() $(\mathcal {T}^*)^{G_{K_v}}=0$
and
$(\mathcal {T}^*)^{G_{K_v}}=0$
and
![]() $\mathcal {T}^*/(\mathcal {T}^*)^{G_{K_v}}$
is a reflexive
$\mathcal {T}^*/(\mathcal {T}^*)^{G_{K_v}}$
is a reflexive
![]() $\Lambda _\infty $
-module, respectively. Since
$\Lambda _\infty $
-module, respectively. Since
![]() $p\ne 2$
, we have
$p\ne 2$
, we have
![]() $(\mathcal {T}^*)^{G_{K_v}}=0$
when v is an Archimedean prime. However, if v is a non-Archimedean prime, it does not split completely in
$(\mathcal {T}^*)^{G_{K_v}}=0$
when v is an Archimedean prime. However, if v is a non-Archimedean prime, it does not split completely in
![]() $K_\infty $
. It follows from [Reference Greenberg12, Lemma 5.2.2] that
$K_\infty $
. It follows from [Reference Greenberg12, Lemma 5.2.2] that
![]() $(\mathcal {T}^*)^{G_{K_v}}=0$
. This guarantees that condition LOC
$(\mathcal {T}^*)^{G_{K_v}}=0$
. This guarantees that condition LOC
![]() $_v^{(1)}(\mathcal {D})$
holds for all
$_v^{(1)}(\mathcal {D})$
holds for all
![]() $v\in \Sigma (K)$
. Finally, as
$v\in \Sigma (K)$
. Finally, as
![]() $\mathcal {T}^*$
is a free
$\mathcal {T}^*$
is a free
![]() $\Lambda _\infty $
-module, condition LOC
$\Lambda _\infty $
-module, condition LOC
![]() $_v^{(2)}(\mathcal {D})$
also holds for all
$_v^{(2)}(\mathcal {D})$
also holds for all
![]() $v\in \Sigma (K)$
.
$v\in \Sigma (K)$
.
We can now state the result due to Greenberg under the condition:
-
(TOR)
 $\mathsf {A}(K)$
has no
$\mathsf {A}(K)$
has no
 $\mathfrak {p}$
-torsion.
$\mathfrak {p}$
-torsion.
Proposition 4.1. If hypotheses (ORD), (TOR) and (CYC) hold, then the
![]() $\Lambda _\infty $
-module
$\Lambda _\infty $
-module
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
does not contain a nontrivial pseudonull submodule.
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
does not contain a nontrivial pseudonull submodule.
Proof. We have verified that conditions RFX(
![]() $\mathcal {D}$
), LEO(
$\mathcal {D}$
), LEO(
![]() $\mathcal {D}$
), CRK
$\mathcal {D}$
), CRK
![]() $(\mathcal {D},\mathcal {L})$
, LOC
$(\mathcal {D},\mathcal {L})$
, LOC
![]() $_v^{(1)}(\mathcal {D})$
and LOC
$_v^{(1)}(\mathcal {D})$
and LOC
![]() $_v^{(2)}(\mathcal {D})$
hold for all
$_v^{(2)}(\mathcal {D})$
hold for all
![]() $v\in \Sigma (K)$
. Next, the condition
$v\in \Sigma (K)$
. Next, the condition
![]() $\mathcal {D}[\mathfrak {m}]$
admits no quotient isomorphic to
$\mathcal {D}[\mathfrak {m}]$
admits no quotient isomorphic to
![]() $\mu _p$
for the action of
$\mu _p$
for the action of
![]() $G_K$
([Reference Greenberg12, Assumption (b)] is equivalent to
$G_K$
([Reference Greenberg12, Assumption (b)] is equivalent to
![]() ${\mathsf {A}(K)[\mathfrak {p}]=0}$
via the Weil pairing (see [Reference Greenberg12, last paragraph on page 248])). Therefore, the result is a direct consequence of [Reference Greenberg, Loeffler and Zerbes13, Proposition 4.1.1].
${\mathsf {A}(K)[\mathfrak {p}]=0}$
via the Weil pairing (see [Reference Greenberg12, last paragraph on page 248])). Therefore, the result is a direct consequence of [Reference Greenberg, Loeffler and Zerbes13, Proposition 4.1.1].
5 Proof of Theorem 1.2
5.1 Preliminary results on Selmer groups
Let
![]() $\mathsf {A}$
be a simple self-dual modular abelian variety of
$\mathsf {A}$
be a simple self-dual modular abelian variety of
![]() $\mathrm {GL}_2$
-type over a totally real field F and let
$\mathrm {GL}_2$
-type over a totally real field F and let
![]() $K/F$
be a CM field.
$K/F$
be a CM field.
Under hypotheses (ORD), (CYC) and (TOR), the structure theorem of finitely generated
![]() $\Lambda _\infty $
-modules (as given in [Reference Bourbaki2, Ch. VII, Section 4, Théorème 5]) combined with Proposition 4.1 asserts the existence of the short exact sequence
$\Lambda _\infty $
-modules (as given in [Reference Bourbaki2, Ch. VII, Section 4, Théorème 5]) combined with Proposition 4.1 asserts the existence of the short exact sequence
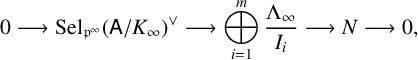 $$ \begin{align} 0 \longrightarrow \mathrm{Sel}_{\mathfrak{p}^\infty}(\mathsf{A}/K_\infty)^\vee \longrightarrow \bigoplus_{i=1}^m\frac{\Lambda_\infty}{I_i} \longrightarrow N \longrightarrow 0, \end{align} $$
$$ \begin{align} 0 \longrightarrow \mathrm{Sel}_{\mathfrak{p}^\infty}(\mathsf{A}/K_\infty)^\vee \longrightarrow \bigoplus_{i=1}^m\frac{\Lambda_\infty}{I_i} \longrightarrow N \longrightarrow 0, \end{align} $$
where
![]() $I_1,\ldots ,I_m $
are principal ideals of
$I_1,\ldots ,I_m $
are principal ideals of
![]() $\Lambda _{\infty }$
and
$\Lambda _{\infty }$
and
![]() $\prod _{i=1}^mI_i=I = \mathrm {char}_{\Lambda _\infty }(\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee )$
is the characteristic ideal of
$\prod _{i=1}^mI_i=I = \mathrm {char}_{\Lambda _\infty }(\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee )$
is the characteristic ideal of
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
as a
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
as a
![]() $\Lambda _\infty $
-module and N is a pseudonull
$\Lambda _\infty $
-module and N is a pseudonull
![]() $\Lambda _\infty $
-module.
$\Lambda _\infty $
-module.
From the discussion in Section 3, there is a unique
![]() $\mathfrak {p}$
-adic L-function
$\mathfrak {p}$
-adic L-function
![]() $L_{\mathfrak {p}}(\mathsf {A})\in F_{\mathfrak {p}} \otimes \Lambda _{\infty }$
associated with the abelian variety
$L_{\mathfrak {p}}(\mathsf {A})\in F_{\mathfrak {p}} \otimes \Lambda _{\infty }$
associated with the abelian variety
![]() $\mathsf {A}$
, which is an analytic object. However, Theorem 1.2 is an assertion involving Selmer groups which are algebraic objects. To bridge this gap, we assume one inclusion of the Iwasawa main conjecture:
$\mathsf {A}$
, which is an analytic object. However, Theorem 1.2 is an assertion involving Selmer groups which are algebraic objects. To bridge this gap, we assume one inclusion of the Iwasawa main conjecture:
-
(h-IMC)
 $L_{\mathfrak {p}}(\mathsf {A}) \in \mathrm {char}_{\Lambda _\infty }(\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee )=\prod _{i=1}^mI_i$
.
$L_{\mathfrak {p}}(\mathsf {A}) \in \mathrm {char}_{\Lambda _\infty }(\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee )=\prod _{i=1}^mI_i$
.
Implicitly, hypothesis (h-IMC) asserts that
![]() $L_{\mathfrak {p}}(\mathsf {A})$
lies inside
$L_{\mathfrak {p}}(\mathsf {A})$
lies inside
![]() $\Lambda _\infty $
. In what follows, set
$\Lambda _\infty $
. In what follows, set
![]() $H_{\mathcal {K}} \simeq \operatorname {Gal}(K_\infty /\mathcal {K})\simeq \mathbb {Z}_p^{\oplus d}$
. When
$H_{\mathcal {K}} \simeq \operatorname {Gal}(K_\infty /\mathcal {K})\simeq \mathbb {Z}_p^{\oplus d}$
. When
![]() $\mathcal {K} = K_{\mathrm {cyc}}$
, we abbreviate
$\mathcal {K} = K_{\mathrm {cyc}}$
, we abbreviate
![]() $H_{K_{\mathrm {cyc}}} = H_{\mathrm {cyc}}$
.
$H_{K_{\mathrm {cyc}}} = H_{\mathrm {cyc}}$
.
Lemma 5.1. Let
![]() $\mathcal {K}$
be a nonanticyclotomic
$\mathcal {K}$
be a nonanticyclotomic
![]() $\mathbb {Z}_p$
-extension of K. If hypotheses (HGT), (ORD), (GHH+
), (TOR) and (h-IMC) hold, then
$\mathbb {Z}_p$
-extension of K. If hypotheses (HGT), (ORD), (GHH+
), (TOR) and (h-IMC) hold, then
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )_{H_{\mathcal {K}}}^\vee $
is a finitely generated torsion
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )_{H_{\mathcal {K}}}^\vee $
is a finitely generated torsion
![]() $\Lambda _{\mathcal {K}}$
-module.
$\Lambda _{\mathcal {K}}$
-module.
Proof. The short exact sequence (5.1) induces the exact sequence
 $$ \begin{align*} H_1(H_{\mathcal{K}}, N) \longrightarrow \mathrm{Sel}_{\mathfrak{p}^\infty}(\mathsf{A}/K_\infty)^{\vee}_{H_{\mathcal{K}}} \longrightarrow\bigoplus_{i=1}^m \frac{\Lambda_{\mathcal{K}}}{\pi_{\mathcal{K}}(I_i)} \longrightarrow H_0(H_{\mathcal{K}}, N) \longrightarrow 0. \end{align*} $$
$$ \begin{align*} H_1(H_{\mathcal{K}}, N) \longrightarrow \mathrm{Sel}_{\mathfrak{p}^\infty}(\mathsf{A}/K_\infty)^{\vee}_{H_{\mathcal{K}}} \longrightarrow\bigoplus_{i=1}^m \frac{\Lambda_{\mathcal{K}}}{\pi_{\mathcal{K}}(I_i)} \longrightarrow H_0(H_{\mathcal{K}}, N) \longrightarrow 0. \end{align*} $$
The inclusion of assumption (h-IMC) combined with Corollary 3.3 implies that
![]() ${\pi _{\mathcal {K}}(I)\ne 0}$
. In particular,
${\pi _{\mathcal {K}}(I)\ne 0}$
. In particular,
![]() ${\Lambda _{\mathcal {K}}}/{\pi _{\mathcal {K}}(I_i)}$
is
${\Lambda _{\mathcal {K}}}/{\pi _{\mathcal {K}}(I_i)}$
is
![]() $\Lambda _{\mathcal {K}}$
-torsion for
$\Lambda _{\mathcal {K}}$
-torsion for
![]() $i=1,\ldots ,m$
. This surjectivity of the last arrow in the exact sequence above implies that
$i=1,\ldots ,m$
. This surjectivity of the last arrow in the exact sequence above implies that
![]() $H_0(H_{\mathcal {K}}, N)$
is
$H_0(H_{\mathcal {K}}, N)$
is
![]() $\Lambda _{\mathcal {K}}$
-torsion. By [Reference Lim24, Proposition 2.3], we conclude that
$\Lambda _{\mathcal {K}}$
-torsion. By [Reference Lim24, Proposition 2.3], we conclude that
![]() $H_1(H_{\mathcal {K}}, N)$
is
$H_1(H_{\mathcal {K}}, N)$
is
![]() $\Lambda _{\mathcal {K}}$
-torsion. Hence, we conclude that
$\Lambda _{\mathcal {K}}$
-torsion. Hence, we conclude that
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )_{H_{\mathcal {K}}}^\vee $
is also a
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )_{H_{\mathcal {K}}}^\vee $
is also a
![]() $\Lambda _{\mathcal {K}}$
-torsion module.
$\Lambda _{\mathcal {K}}$
-torsion module.
Proposition 5.2. Write
![]() $\mathcal {K}/K$
to denote a
$\mathcal {K}/K$
to denote a
![]() $\mathbb {Z}_p$
-extension and let
$\mathbb {Z}_p$
-extension and let
![]() $H_{\mathcal {K}}$
denote the Galois group
$H_{\mathcal {K}}$
denote the Galois group
![]() $\operatorname {Gal}(K_\infty /\mathcal {K})\simeq \mathbb {Z}_p^{\oplus d}$
. Suppose that hypotheses (TOR) and (ORD) are satisfied. Then, the restriction map
$\operatorname {Gal}(K_\infty /\mathcal {K})\simeq \mathbb {Z}_p^{\oplus d}$
. Suppose that hypotheses (TOR) and (ORD) are satisfied. Then, the restriction map
is injective. When
![]() $\mathcal {K} = K_{\mathrm {cyc}}$
, the cokernel of
$\mathcal {K} = K_{\mathrm {cyc}}$
, the cokernel of
![]() $\alpha $
is a torsion
$\alpha $
is a torsion
![]() $\Lambda _{\mathrm {cyc}}$
-module. In particular,
$\Lambda _{\mathrm {cyc}}$
-module. In particular,
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )_{H_{\mathrm {cyc}}}^\vee $
is a torsion
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )_{H_{\mathrm {cyc}}}^\vee $
is a torsion
![]() $\Lambda _{\mathrm {cyc}}$
-module if and only if
$\Lambda _{\mathrm {cyc}}$
-module if and only if
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
is a torsion
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
is a torsion
![]() $\Lambda _{\mathrm {cyc}}$
-module.
$\Lambda _{\mathrm {cyc}}$
-module.
We note that this result does not require any hypothesis on the reduction type at primes
![]() $v\mid p$
.
$v\mid p$
.
Proof. We begin by recalling the fundamental diagram
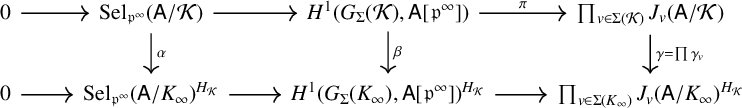
where the vertical maps are given by restriction. To prove the first assertion, we study the leftmost downward arrow and obtain the exact sequence
Note that
where the description of
![]() $\ker (\beta )$
comes from inflation-restriction. Since our assumptions imply that
$\ker (\beta )$
comes from inflation-restriction. Since our assumptions imply that
![]() $\mathsf {A}(K)[\mathfrak {p}]=0$
, it follows that
$\mathsf {A}(K)[\mathfrak {p}]=0$
, it follows that
![]() $\mathsf {A}(K_\infty )[\mathfrak {p}]=0$
(see, for example, [Reference Neukirch, Schmidt and Wingberg30, I.6.13]). Thus,
$\mathsf {A}(K_\infty )[\mathfrak {p}]=0$
(see, for example, [Reference Neukirch, Schmidt and Wingberg30, I.6.13]). Thus,
![]() $\ker (\alpha )=\ker (\beta )=0$
. The result is now immediate from our assumption that
$\ker (\alpha )=\ker (\beta )=0$
. The result is now immediate from our assumption that
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )_{H_{\mathcal {K}}}^\vee $
is a
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )_{H_{\mathcal {K}}}^\vee $
is a
![]() $\Lambda _{\mathcal {K}}$
-torsion module.
$\Lambda _{\mathcal {K}}$
-torsion module.
Next, we observe that the same argument yields
To complete the proof, it suffices to show that
Note that
![]() $v\mid \mathfrak {p}$
is deeply ramified in the sense of Coates–Greenberg. Imitating the proof of [Reference Coates and Greenberg5, Proposition 4.8], when
$v\mid \mathfrak {p}$
is deeply ramified in the sense of Coates–Greenberg. Imitating the proof of [Reference Coates and Greenberg5, Proposition 4.8], when
![]() $v\mid \mathfrak {p}$
has good ordinary reduction,
$v\mid \mathfrak {p}$
has good ordinary reduction,
 $$ \begin{align*} \ker(\gamma) = \prod \ker(\gamma_v) = \prod_{\substack{v \in \Sigma(\mathcal{K})\\ v \nmid \mathfrak{p}}} H^1(H_{w},\mathsf{A}(K_{\infty,w})[\mathfrak{p}^\infty]) \times \prod_{\substack{v \in \Sigma(\mathcal{K})\\ v\mid \mathfrak{p}}} H^1(H_{w},\widetilde{\mathsf{A}}(k_{w})[\mathfrak{p}^\infty]), \end{align*} $$
$$ \begin{align*} \ker(\gamma) = \prod \ker(\gamma_v) = \prod_{\substack{v \in \Sigma(\mathcal{K})\\ v \nmid \mathfrak{p}}} H^1(H_{w},\mathsf{A}(K_{\infty,w})[\mathfrak{p}^\infty]) \times \prod_{\substack{v \in \Sigma(\mathcal{K})\\ v\mid \mathfrak{p}}} H^1(H_{w},\widetilde{\mathsf{A}}(k_{w})[\mathfrak{p}^\infty]), \end{align*} $$
where
![]() $w=w_v$
denotes any place of
$w=w_v$
denotes any place of
![]() $K_\infty $
lying above v,
$K_\infty $
lying above v,
![]() $H_{w}$
denotes the decomposition group of w inside
$H_{w}$
denotes the decomposition group of w inside
![]() $H_{\mathcal {K}}$
,
$H_{\mathcal {K}}$
,
![]() $\widetilde {\mathsf {A}}$
denotes the reduction of
$\widetilde {\mathsf {A}}$
denotes the reduction of
![]() $\mathsf {A}$
modulo w and
$\mathsf {A}$
modulo w and
![]() $k_{w}$
denotes the residue field of
$k_{w}$
denotes the residue field of
![]() $K_\infty $
at w.
$K_\infty $
at w.
For the remainder of the argument, we assume that
![]() $\mathcal {K} = K_{\mathrm {cyc}}$
. First, we consider the case
$\mathcal {K} = K_{\mathrm {cyc}}$
. First, we consider the case
![]() $v\nmid \mathfrak {p}$
. In this case, the local map
$v\nmid \mathfrak {p}$
. In this case, the local map
![]() $\gamma _v$
is simply the identity map: for any
$\gamma _v$
is simply the identity map: for any
![]() $v \in \Sigma (K_{\mathrm {cyc}})$
such that
$v \in \Sigma (K_{\mathrm {cyc}})$
such that
![]() $v\nmid \mathfrak {p}$
and any place w of
$v\nmid \mathfrak {p}$
and any place w of
![]() $K_\infty $
lying above v, we see that
$K_\infty $
lying above v, we see that
![]() $K_{\infty ,w}=K_{\mathrm {cyc},v}$
is the unique
$K_{\infty ,w}=K_{\mathrm {cyc},v}$
is the unique
![]() $\mathbb {Z}_p$
-extension of
$\mathbb {Z}_p$
-extension of
![]() $K_{\mathfrak {p}'}$
, where
$K_{\mathfrak {p}'}$
, where
![]() $\mathfrak {p}'$
is the place of K lying below v. In other words,
$\mathfrak {p}'$
is the place of K lying below v. In other words,
![]() $\ker (\gamma _v)=0$
.
$\ker (\gamma _v)=0$
.
When
![]() $v\mid \mathfrak {p}$
and
$v\mid \mathfrak {p}$
and
![]() $\mathfrak {p}$
is a prime of good ordinary reduction, it suffices to know that
$\mathfrak {p}$
is a prime of good ordinary reduction, it suffices to know that
![]() $\widetilde {\mathsf {A}}(k_w)[\mathfrak {p}^\infty ]$
itself is cotorsion (since it is of finite corank over
$\widetilde {\mathsf {A}}(k_w)[\mathfrak {p}^\infty ]$
itself is cotorsion (since it is of finite corank over
![]() $\mathcal {O}_{\mathfrak {p}}$
). However, when
$\mathcal {O}_{\mathfrak {p}}$
). However, when
![]() $\mathfrak {p}$
is a prime of potentially ordinary reduction,
$\mathfrak {p}$
is a prime of potentially ordinary reduction,
![]() $\ker (\gamma _v) = H^1(H_w, D)$
, where
$\ker (\gamma _v) = H^1(H_w, D)$
, where
![]() $D = \mathsf {A}[\mathfrak {p}^\infty ]/C$
and C is a formal group (over a base extension). In any case, the kernel lies inside
$D = \mathsf {A}[\mathfrak {p}^\infty ]/C$
and C is a formal group (over a base extension). In any case, the kernel lies inside
![]() $H^1(K_{\infty ,v},\mathsf {A}[\mathfrak {p}^\infty ])$
. As a
$H^1(K_{\infty ,v},\mathsf {A}[\mathfrak {p}^\infty ])$
. As a
![]() $\Lambda _{\mathrm {cyc}}$
-module, we note that
$\Lambda _{\mathrm {cyc}}$
-module, we note that
![]() $\mathsf {A}[\mathfrak {p}^\infty ]$
is still cotorsion. So,
$\mathsf {A}[\mathfrak {p}^\infty ]$
is still cotorsion. So,
![]() $H^1(K_{\infty ,v},\mathsf {A}[\mathfrak {p}^\infty ])$
, and hence
$H^1(K_{\infty ,v},\mathsf {A}[\mathfrak {p}^\infty ])$
, and hence
![]() $\ker (\gamma _v)$
, is
$\ker (\gamma _v)$
, is
![]() $\Lambda _{\mathrm {cyc}}$
-cotorsion. Here, we crucially use the fact that
$\Lambda _{\mathrm {cyc}}$
-cotorsion. Here, we crucially use the fact that
![]() $v\mid \mathfrak {p}$
is finitely decomposed in the cyclotomic
$v\mid \mathfrak {p}$
is finitely decomposed in the cyclotomic
![]() $\mathbb {Z}_p$
-extension.
$\mathbb {Z}_p$
-extension.
5.2 The (non)-growth of Selmer coranks
We are now ready to conclude the proof of Theorem 1.2, which is divided into two steps. The first step is to show that the Selmer corank is bounded in a nonanticyclotomic
![]() $\mathbb {Z}_p$
-extension of K using the preliminary results from the previous sections. The second step is to show that the Selmer corank grows, as predicted, in an anticyclotomic
$\mathbb {Z}_p$
-extension of K using the preliminary results from the previous sections. The second step is to show that the Selmer corank grows, as predicted, in an anticyclotomic
![]() $\mathbb {Z}_p$
-extension of K. The main input will be results of Nekovář [Reference Nekovář28, Reference Nekovář, Burns, Buzzard and Nekovář29] on the Heegner point Euler system and the parity conjecture.
$\mathbb {Z}_p$
-extension of K. The main input will be results of Nekovář [Reference Nekovář28, Reference Nekovář, Burns, Buzzard and Nekovář29] on the Heegner point Euler system and the parity conjecture.
Theorem 5.3. Let
![]() $\mathsf {A}$
be a simple modular self-dual abelian variety of
$\mathsf {A}$
be a simple modular self-dual abelian variety of
![]() $\mathrm {GL}_2$
-type over a totally real field F with trivial central character and let K be a totally imaginary extension of F, satisfying hypotheses (ORD), (GHH+
), (TOR), (h-IMC) and (HGT). If
$\mathrm {GL}_2$
-type over a totally real field F with trivial central character and let K be a totally imaginary extension of F, satisfying hypotheses (ORD), (GHH+
), (TOR), (h-IMC) and (HGT). If
![]() $\mathcal {K}$
is a nonanticyclotomic
$\mathcal {K}$
is a nonanticyclotomic
![]() $\mathbb {Z}_p$
-extension of K and
$\mathbb {Z}_p$
-extension of K and
![]() $\mathcal {K}_n$
is the nth layer of the
$\mathcal {K}_n$
is the nth layer of the
![]() $\mathbb {Z}_p$
-extension, then
$\mathbb {Z}_p$
-extension, then
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K}_n)^\vee $
is bounded as
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K}_n)^\vee $
is bounded as
![]() $n\rightarrow \infty $
.
$n\rightarrow \infty $
.
Proof. In light of Theorem 2.2 and Corollary 2.3, it suffices to prove that
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K})^\vee $
is
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K})^\vee $
is
![]() $\Lambda _{\mathcal {K}}$
-torsion. By Proposition 5.2, there is a surjection
$\Lambda _{\mathcal {K}}$
-torsion. By Proposition 5.2, there is a surjection
Furthermore, it follows from Lemma 5.1 that
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee _{H_{\mathcal {K}}}$
is
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee _{H_{\mathcal {K}}}$
is
![]() $\Lambda _{\mathcal {K}}$
-torsion. Hence, we deduce that
$\Lambda _{\mathcal {K}}$
-torsion. Hence, we deduce that
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K})^\vee $
is
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K})^\vee $
is
![]() $\Lambda _{\mathcal {K}}$
-torsion, as desired.
$\Lambda _{\mathcal {K}}$
-torsion, as desired.
Theorem 5.4. Let
![]() $\mathsf {A}$
be a simple modular self-dual abelian variety of
$\mathsf {A}$
be a simple modular self-dual abelian variety of
![]() $\mathrm {GL}_2$
-type over a totally real field F with trivial central character and let K be a totally imaginary extension of F, satisfying hypotheses (ORD), (GHH+
) and (HGT). Let
$\mathrm {GL}_2$
-type over a totally real field F with trivial central character and let K be a totally imaginary extension of F, satisfying hypotheses (ORD), (GHH+
) and (HGT). Let
![]() $\mathcal {K}$
be a
$\mathcal {K}$
be a
![]() $\mathbb {Z}_p$
-extension of K that lies inside
$\mathbb {Z}_p$
-extension of K that lies inside
![]() $K_{\mathrm {ac}}$
and set
$K_{\mathrm {ac}}$
and set
![]() $\mathcal {K}_n$
to denote the nth layer of the
$\mathcal {K}_n$
to denote the nth layer of the
![]() $\mathbb {Z}_p$
-extension
$\mathbb {Z}_p$
-extension
![]() $\mathcal {K}/K$
. Then,
$\mathcal {K}/K$
. Then,
Proof. Under hypothesis (HGT),
![]() $z_{\mathrm {Heeg}}$
is not a torsion element of
$z_{\mathrm {Heeg}}$
is not a torsion element of
![]() $\mathsf {A}(K)$
. In particular, the main theorem of [Reference Nekovář, Burns, Buzzard and Nekovář29] implies that
$\mathsf {A}(K)$
. In particular, the main theorem of [Reference Nekovář, Burns, Buzzard and Nekovář29] implies that ![]() is finite and the
is finite and the
![]() $\mathcal {O}_{\mathfrak {p}}$
-module generated by
$\mathcal {O}_{\mathfrak {p}}$
-module generated by
![]() $z_{\mathrm {Heeg}}$
inside
$z_{\mathrm {Heeg}}$
inside
![]() $\mathsf {A}(K)$
is an
$\mathsf {A}(K)$
is an
![]() $\mathcal {O}_{\mathfrak {p}}$
-module of rank one. Therefore,
$\mathcal {O}_{\mathfrak {p}}$
-module of rank one. Therefore,
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)$
is of corank one over
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)$
is of corank one over
![]() $\mathcal {O}_{\mathfrak {p}}$
. As the restriction map
$\mathcal {O}_{\mathfrak {p}}$
. As the restriction map
has finite kernel and cokernel by Theorem 2.2, it follows that
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K})^\vee $
is of rank one or zero over
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K})^\vee $
is of rank one or zero over
![]() $\Lambda _{\mathcal {K}}$
. However, since the root number of
$\Lambda _{\mathcal {K}}$
. However, since the root number of
![]() $\mathsf {A}$
over
$\mathsf {A}$
over
![]() $\mathcal {K}_n$
is
$\mathcal {K}_n$
is
![]() $-1$
by hypothesis (GHH+
), it follows from [Reference Nekovář28, Theorem 0.4] that the
$-1$
by hypothesis (GHH+
), it follows from [Reference Nekovář28, Theorem 0.4] that the
![]() $\mathcal {O}_{\mathfrak {p}}$
-corank of
$\mathcal {O}_{\mathfrak {p}}$
-corank of
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K}_n)$
is unbounded as
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K}_n)$
is unbounded as
![]() $n\to \infty $
. By Corollary 2.3, the
$n\to \infty $
. By Corollary 2.3, the
![]() $\Lambda _{\mathcal {K}}$
-corank of
$\Lambda _{\mathcal {K}}$
-corank of
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K})$
is one and
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K})$
is one and
![]() $\mathrm {corank}_{\mathcal {O}_{\mathfrak {p}}}\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K}_n)=p^n+O(1)$
, as desired.
$\mathrm {corank}_{\mathcal {O}_{\mathfrak {p}}}\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K}_n)=p^n+O(1)$
, as desired.
6 Proof of Theorem 1.3
The main goal of this section is to prove Theorem 1.3. We adopt the method of [Reference Gajek-Leonard, Hatley, Kundu and Lei8], removing the nonanomalous hypothesis and streamlining the use of the control theorem. Instead of hypothesis (HGT) in the previous section, we consider the following hypotheses.
-
(S-C) The
 $\Lambda _\infty $
-module
$\Lambda _\infty $
-module
 $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
is a direct sum of cyclic
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_\infty )^\vee $
is a direct sum of cyclic
 $\Lambda _\infty $
modules.
$\Lambda _\infty $
modules. -
(RK) The order of vanishing of
 $\mathrm {char}_{\Lambda _{\mathrm {cyc}}}\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
at
$\mathrm {char}_{\Lambda _{\mathrm {cyc}}}\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
at
 $X_0$
is at most one.
$X_0$
is at most one.
Theorem 6.1. Let
![]() $\mathsf {A}$
be a simple modular self-dual abelian variety of
$\mathsf {A}$
be a simple modular self-dual abelian variety of
![]() $\mathrm {GL}_2$
-type over a totally real field F with trivial central character satisfying hypothesis (ORD). Let
$\mathrm {GL}_2$
-type over a totally real field F with trivial central character satisfying hypothesis (ORD). Let
![]() $K/F$
be a totally imaginary extension and
$K/F$
be a totally imaginary extension and
![]() $\mathcal {K}/K$
be a
$\mathcal {K}/K$
be a
![]() $\mathbb {Z}_p$
-extension. Suppose that assumption (CYC) and either of the following conditions holds:
$\mathbb {Z}_p$
-extension. Suppose that assumption (CYC) and either of the following conditions holds:
-
(i) the order of vanishing of
 $\mathrm {char}_{\Lambda _{\mathrm {cyc}}}\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
at
$\mathrm {char}_{\Lambda _{\mathrm {cyc}}}\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
at
 $X_0$
is zero;
$X_0$
is zero; -
(ii) hypothesis (S-C) holds and
 $\mathcal {K}$
is a nonanticyclotomic
$\mathcal {K}$
is a nonanticyclotomic
 $\mathbb {Z}_p$
-extension of K.
$\mathbb {Z}_p$
-extension of K.
Then,
![]() $\mathrm {rank}_{\mathcal {O}_{\mathfrak {p}}}\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K}_n)^\vee $
is bounded as
$\mathrm {rank}_{\mathcal {O}_{\mathfrak {p}}}\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K}_n)^\vee $
is bounded as
![]() $n\rightarrow \infty $
.
$n\rightarrow \infty $
.
Proof. In case (i), it follows from Theorem 2.2 that
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)$
is finite; hence,
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)$
is finite; hence,
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K})^\vee $
is
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K})^\vee $
is
![]() $\Lambda _{\mathcal {K}}$
-torsion. By Corollary 2.3, we conclude that the
$\Lambda _{\mathcal {K}}$
-torsion. By Corollary 2.3, we conclude that the
![]() $\mathcal {O}_{\mathfrak {p}}$
-rank of
$\mathcal {O}_{\mathfrak {p}}$
-rank of
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K}_n)^\vee $
is bounded as
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K}_n)^\vee $
is bounded as
![]() $n\rightarrow \infty $
.
$n\rightarrow \infty $
.
For the remainder of the proof, we consider case (ii). In particular, hypothesis (S-C) holds, which means that the pseudonull module N in (5.1) is trivial. Let
![]() $f_i\in \Lambda _\infty $
be a generator of
$f_i\in \Lambda _\infty $
be a generator of
![]() $I_i$
. Let us write
$I_i$
. Let us write
 $$ \begin{align*} f_i=\sum_{k=0}^\infty G_{i,k}(X_1,\ldots, X_d)X_0^k, \end{align*} $$
$$ \begin{align*} f_i=\sum_{k=0}^\infty G_{i,k}(X_1,\ldots, X_d)X_0^k, \end{align*} $$
where ![]() . By Proposition 5.2, there is a surjection
. By Proposition 5.2, there is a surjection
 $$ \begin{align} ( \mathrm{Sel}_{\mathfrak{p}^\infty}(\mathsf{A}/K_\infty)^\vee)_{H_{\mathcal{K}}}\simeq\bigoplus_{i=1}^m\frac{\Lambda_{\mathcal{K}}}{\left(\pi_{\mathcal{K}}(f_i)\right)}\twoheadrightarrow\mathrm{Sel}_{\mathfrak{p}^\infty}(\mathsf{A}/\mathcal{K})^\vee. \end{align} $$
$$ \begin{align} ( \mathrm{Sel}_{\mathfrak{p}^\infty}(\mathsf{A}/K_\infty)^\vee)_{H_{\mathcal{K}}}\simeq\bigoplus_{i=1}^m\frac{\Lambda_{\mathcal{K}}}{\left(\pi_{\mathcal{K}}(f_i)\right)}\twoheadrightarrow\mathrm{Sel}_{\mathfrak{p}^\infty}(\mathsf{A}/\mathcal{K})^\vee. \end{align} $$
Thus,
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K})^\vee $
is
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K})^\vee $
is
![]() $\Lambda _{\mathcal {K}}$
-torsion if
$\Lambda _{\mathcal {K}}$
-torsion if
![]() $\pi _{\mathcal {K}}(f_i)\ne 0$
for all
$\pi _{\mathcal {K}}(f_i)\ne 0$
for all
![]() $i=1,\ldots , m$
.
$i=1,\ldots , m$
.
When
![]() $\mathcal {K}=K_{\mathrm {cyc}}$
, Proposition 5.2 says that the kernel in (6.1) is
$\mathcal {K}=K_{\mathrm {cyc}}$
, Proposition 5.2 says that the kernel in (6.1) is
![]() $\Lambda _{\mathrm {cyc}}$
-torsion. Thus, by invoking assumption (CYC),
$\Lambda _{\mathrm {cyc}}$
-torsion. Thus, by invoking assumption (CYC),
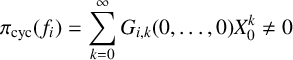 $$ \begin{align*} \pi_{\mathrm{cyc}}(f_i)=\sum_{k=0}^\infty G_{i,k}(0,\ldots, 0)X_0^k\ne0 \end{align*} $$
$$ \begin{align*} \pi_{\mathrm{cyc}}(f_i)=\sum_{k=0}^\infty G_{i,k}(0,\ldots, 0)X_0^k\ne0 \end{align*} $$
for
![]() $i\in \{1,\ldots ,m\}$
. In particular, there is an integer
$i\in \{1,\ldots ,m\}$
. In particular, there is an integer
![]() $m(i)$
such that
$m(i)$
such that
![]() $G_{i,m(i)}(0,\ldots , 0)\ne 0$
, with
$G_{i,m(i)}(0,\ldots , 0)\ne 0$
, with
![]() $G_{i,k}(0,\ldots , 0)= 0$
for all
$G_{i,k}(0,\ldots , 0)= 0$
for all
![]() $k< m(i)$
.
$k< m(i)$
.
Let
![]() $\mathcal {K}$
be a
$\mathcal {K}$
be a
![]() $\mathbb {Z}_p$
-extension of K which is not an anticyclotomic extension. Recall that
$\mathbb {Z}_p$
-extension of K which is not an anticyclotomic extension. Recall that
![]() $\mathcal {K}$
corresponds to
$\mathcal {K}$
corresponds to
![]() $(c_0:\cdots :c_d)\in \mathbb {P}^d(\mathbb {Z}_p)$
with
$(c_0:\cdots :c_d)\in \mathbb {P}^d(\mathbb {Z}_p)$
with
![]() $c_0\ne 0$
. In particular,
$c_0\ne 0$
. In particular,
Therefore,
 $$ \begin{align*} & \pi_{\mathcal{K}}(f_i)=\sum_{k\ge m(i)}G_{i,k}((1+X_{\mathcal{K}})^{{c_1}/{c_j(\mathcal{K})}}-1,\ldots, (1+X_{\mathcal{K}})^{{c_d}/{c_j(\mathcal{K})}}-1)\pi_{\mathcal{K}}(X_0)^k\\ &\quad =G_{i,m(i)}((1+X_{\mathcal{K}})^{{c_1}/{c_j(\mathcal{K})}}-1,\ldots, (1+X_{\mathcal{K}})^{{c_d}/{c_j(\mathcal{K})}}-1)\bigg(\frac{c_0}{c_j(\mathcal{K})}X_{\mathcal{K}}\bigg)^{m(i)}+O(X_{\mathcal{K}}^{m(i)+1})\\ &\quad =G_{i,m(i)}(0,\ldots, 0)\bigg(\frac{c_0}{c_j(\mathcal{K})}X_{\mathcal{K}}\bigg)^{m(i)}+O(X_{\mathcal{K}}^{m(i)+1}) \ne0. \end{align*} $$
$$ \begin{align*} & \pi_{\mathcal{K}}(f_i)=\sum_{k\ge m(i)}G_{i,k}((1+X_{\mathcal{K}})^{{c_1}/{c_j(\mathcal{K})}}-1,\ldots, (1+X_{\mathcal{K}})^{{c_d}/{c_j(\mathcal{K})}}-1)\pi_{\mathcal{K}}(X_0)^k\\ &\quad =G_{i,m(i)}((1+X_{\mathcal{K}})^{{c_1}/{c_j(\mathcal{K})}}-1,\ldots, (1+X_{\mathcal{K}})^{{c_d}/{c_j(\mathcal{K})}}-1)\bigg(\frac{c_0}{c_j(\mathcal{K})}X_{\mathcal{K}}\bigg)^{m(i)}+O(X_{\mathcal{K}}^{m(i)+1})\\ &\quad =G_{i,m(i)}(0,\ldots, 0)\bigg(\frac{c_0}{c_j(\mathcal{K})}X_{\mathcal{K}}\bigg)^{m(i)}+O(X_{\mathcal{K}}^{m(i)+1}) \ne0. \end{align*} $$
It follows that
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K})^\vee $
is
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K})^\vee $
is
![]() $\Lambda _{\mathcal {K}}$
-torsion and, from Corollary 2.3, the
$\Lambda _{\mathcal {K}}$
-torsion and, from Corollary 2.3, the
![]() $\mathcal {O}_{\mathfrak {p}}$
-rank of
$\mathcal {O}_{\mathfrak {p}}$
-rank of
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K}_n)^\vee $
is bounded as
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/\mathcal {K}_n)^\vee $
is bounded as
![]() $n\rightarrow \infty $
.
$n\rightarrow \infty $
.
Theorem 6.2. Let
![]() $\mathsf {A}$
be as in Theorem 6.1. Suppose that hypotheses (ORD), (GHH+
), (CYC) and (RK) hold. If
$\mathsf {A}$
be as in Theorem 6.1. Suppose that hypotheses (ORD), (GHH+
), (CYC) and (RK) hold. If
![]() $\mathcal {K}$
is a
$\mathcal {K}$
is a
![]() $\mathbb {Z}_p$
-extension of K that lies inside
$\mathbb {Z}_p$
-extension of K that lies inside
![]() $K_{\mathrm {ac}}$
, then
$K_{\mathrm {ac}}$
, then
Proof. As in the proof of Theorem 5.4, it suffices to show that
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)^\vee $
is of corank one over
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)^\vee $
is of corank one over
![]() $\mathcal {O}_{\mathfrak {p}}$
. Indeed, under hypothesis (GHH+
), the corank of
$\mathcal {O}_{\mathfrak {p}}$
. Indeed, under hypothesis (GHH+
), the corank of
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)^\vee $
is nonzero by [Reference Nekovář, Burns, Buzzard and Nekovář29, Theorem 0.4]. Therefore, combined with hypothesis (RK), the order of vanishing of
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)^\vee $
is nonzero by [Reference Nekovář, Burns, Buzzard and Nekovář29, Theorem 0.4]. Therefore, combined with hypothesis (RK), the order of vanishing of
![]() $\mathrm {char}_{\Lambda _{\mathrm {cyc}}}\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
at
$\mathrm {char}_{\Lambda _{\mathrm {cyc}}}\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K_{\mathrm {cyc}})^\vee $
at
![]() $X_0$
is exactly one. Thus, Theorem 2.2 implies that
$X_0$
is exactly one. Thus, Theorem 2.2 implies that
![]() $\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)^\vee $
is of corank one over
$\mathrm {Sel}_{\mathfrak {p}^\infty }(\mathsf {A}/K)^\vee $
is of corank one over
![]() $\mathcal {O}_{\mathfrak {p}}$
, as desired.
$\mathcal {O}_{\mathfrak {p}}$
, as desired.
Acknowledgements
We thank Henri Darmon and Daniel Disegni for answering our questions during the preparation of this article.