No CrossRef data available.
Article contents
FITTING SUBGROUP AND NILPOTENT RESIDUAL OF FIXED POINTS
Part of:
Representation theory of groups
Published online by Cambridge University Press: 26 December 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 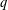 $q$ be a prime and let
$q$ be a prime and let 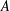 $A$ be an elementary abelian group of order at least
$A$ be an elementary abelian group of order at least 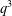 $q^{3}$ acting by automorphisms on a finite
$q^{3}$ acting by automorphisms on a finite 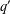 $q^{\prime }$-group
$q^{\prime }$-group 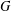 $G$. We prove that if
$G$. We prove that if 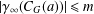 $|\unicode[STIX]{x1D6FE}_{\infty }(C_{G}(a))|\leq m$ for any
$|\unicode[STIX]{x1D6FE}_{\infty }(C_{G}(a))|\leq m$ for any 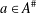 $a\in A^{\#}$, then the order of
$a\in A^{\#}$, then the order of 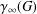 $\unicode[STIX]{x1D6FE}_{\infty }(G)$ is
$\unicode[STIX]{x1D6FE}_{\infty }(G)$ is 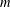 $m$-bounded. If
$m$-bounded. If 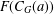 $F(C_{G}(a))$ has index at most
$F(C_{G}(a))$ has index at most 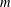 $m$ in
$m$ in 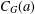 $C_{G}(a)$ for any
$C_{G}(a)$ for any 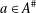 $a\in A^{\#}$, then the index of
$a\in A^{\#}$, then the index of 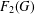 $F_{2}(G)$ is
$F_{2}(G)$ is 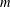 $m$-bounded.
$m$-bounded.
MSC classification
Primary:
20D45: Automorphisms
Information
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
Footnotes
The first author was supported by FEMAT; the second author was supported by FAPDF and CNPq-Brazil.
References
Acciarri, C., Shumyatsky, P. and Thillaisundaram, A., ‘Conciseness of coprime commutators in finite groups’, Bull. Aust. Math. Soc.
89 (2014), 252–258.Google Scholar
de Melo, E., Lima, A. S. and Shumyatsky, P., ‘Nilpotent residual of fixed points’, Arc. Math.
111 (2018), 13–21.Google Scholar
de Melo, E. and Shumyatsky, P., ‘Finite groups and their coprime automorphisms’, Proc. Amer. Math. Soc.
145 (2017), 3755–3760.Google Scholar
Goldschmidt, D. M., ‘Weakly embedded 2-local subgroups of finite groups’, J. Algebra
21 (1972), 341–351.10.1016/0021-8693(72)90028-2Google Scholar
Guralnick, R. and Shumyatsky, P., ‘Derived subgroups of fixed points’, Israel J. Math.
126 (2001), 345–362.10.1007/BF02784161Google Scholar
Khukhro, E. I., Nilpotent Groups and their Automorphisms (de Gruyter, Berlin–New York, 1993).Google Scholar
Shumyatsky, P., ‘Finite groups and the fixed points of coprime automorphisms’, Proc. Amer. Math. Soc.
129 (2001), 3479–3484.Google Scholar
Shumyatsky, P., ‘Positive laws in fixed points’, Trans. Amer. Math. Soc.
356 (2003), 2081–2091.Google Scholar
Shumyatsky, P., ‘Linear groups with almost right Engel elements’, Proc. Edinb. Math. Soc., to appear.Google Scholar
Ward, J. N., ‘On finite groups admitting automorphisms with nilpotent fixed-point’, Bull. Aust. Math. Soc.
5 (1971), 281–282.Google Scholar

