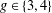Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jin, Wei
2017.
Two-geodesic-transitive graphs which are locally connected.
Discrete Mathematics,
Vol. 340,
Issue. 4,
p.
637.
Feng, Rongquan
and
Hua, Peice
2018.
A new family of Geodesic transitive graphs.
Discrete Mathematics,
Vol. 341,
Issue. 10,
p.
2700.
Jin, Wei
2018.
The pentavalent three-geodesic-transitive graphs.
Discrete Mathematics,
Vol. 341,
Issue. 5,
p.
1344.
Jin, Wei
and
Praeger, Cheryl E.
2021.
Normal quotients of diameter at most two of finite three-geodesic-transitive graphs.
Journal of Combinatorial Theory, Series A,
Vol. 178,
Issue. ,
p.
105349.
Jin, Wei
and
Tan, Li
2022.
Two-geodesic-transitive graphs which are locally self-complementary.
Discrete Mathematics,
Vol. 345,
Issue. 8,
p.
112900.
Jin, Wei
and
Tan, Li
2024.
Finite 4-geodesic-transitive graphs with bounded girth.
Journal of Algebraic Combinatorics,
Vol. 60,
Issue. 4,
p.
949.