Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-11T12:43:16.826Z Has data issue: false hasContentIssue false
  • English
  • Français

EXISTENCE OF K-MULTIMAGIC SQUARES AND MAGIC SQUARES OF kth POWERS WITH DISTINCT ENTRIES

Part of: Designs and configurations Diophantine equations Exponential sums and character sums Forms and linear algebraic groups Additive number theory; partitions

Published online by Cambridge University Press:  11 February 2025

DANIEL FLORES Open the ORCID record for DANIEL FLORES [Opens in a new window]
DANIEL FLORES*
Affiliation:
Department of Mathematics, Purdue University, 150 N. University Street, West Lafayette, IN 47907-2067, USA
*
e-mail: flore205@purdue.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We demonstrate the existence of K-multimagic squares of order N consisting of 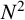$N^2$ distinct integers whenever 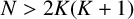$N> 2K(K+1)$. This improves our earlier result [D. Flores, ‘A circle method approach to K-multimagic squares’, preprint (2024), arXiv:2406.08161] in which we only required 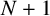$N+1$ distinct integers. Additionally, we present a direct method by which our analysis of the magic square system may be used to show the existence of $N \times N$ magic squares consisting of distinct kth powers when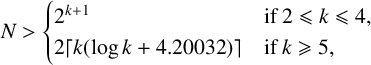

$$ \begin{align*}N> \begin{cases} 2^{k+1} & \text{if}\ 2 \leqslant k \leqslant 4, \\ 2 \lceil k(\log k + 4.20032) \rceil & \text{if}\ k \geqslant 5, \end{cases}\end{align*} $$

improving on a recent result by Rome and Yamagishi [‘On the existence of magic squares of powers’, preprint (2024), arxiv:2406.09364].

Keywords

Hardy–Littlewood methodadditive forms in differing degreesmagic squaresmultimagic squares

MSC classification

Primary: 11P55: Applications of the Hardy-Littlewood method
Secondary: 05B15: Orthogonal arrays, Latin squares, Room squares 05B20: Matrices (incidence, Hadamard, etc.) 11D45: Counting solutions of Diophantine equations 11D72: Equations in many variables 11E76: Forms of degree higher than two 11L07: Estimates on exponential sums
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 8
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author acknowledges the support of Purdue University, which provided funding for this research through the Ross–Lynn Research Scholar Fund.

References

Boyer, C., Highly Multimagic Squares, accessed 31 October 2024. http://www.multimagie.com/English/HighlyMultimagic.htm.Google Scholar
Bremner, A., ‘On squares of squares’, Acta Arith. 88(3) (1999), 289–297.CrossRefGoogle Scholar
Bremner, A., ‘On squares of squares. II’, Acta Arith. 99(3) (2001), 289–308.CrossRefGoogle Scholar
Derksen, H., Eggermont, C. and van den Essen, A., ‘Multimagic squares’, Amer. Math. Monthly 114(8) (2007), 703–713.CrossRefGoogle Scholar
Flores, D., ‘A circle method approach to $K$ -multimagic squares’, Preprint, 2024, arXiv:2406.08161.Google Scholar
Low, L., Pitman, J. and Wolff, A., ‘Simultaneous diagonal congruences’, J. Number Theory 29(1) (1988), 31–59.CrossRefGoogle Scholar
Rome, N. and Yamagishi, S., ‘On the existence of magic squares of powers’, Preprint, 2024, arXiv:2406.09364.Google Scholar
Rome, N. and Yamagishi, S., ‘Integral solutions to systems of diagonal equations’, Preprint, 2024, arXiv:2406.09256.Google Scholar
Trump, W., Trimagic Squares of Order 12, accessed 13 December 2024. https://www.trump.de/magic-squares/trimagic/12x12-trimagic-0001a.pdf.Google Scholar
Zhang, Y., Chen, K. and Lei, J., ‘Large sets of orthogonal arrays and multimagic squares’, J. Combin. Des. 21(9) (2013), 390–403.CrossRefGoogle Scholar
Zhang, Y., Chen, K. and Li, W., ‘A family of multimagic squares based on large sets of orthogonal arrays’, Ars Combin. 144 (2019), 35–47.Google Scholar