Hostname: page-component-cb9f654ff-h4f6x Total loading time: 0 Render date: 2025-08-22T07:31:54.881Z Has data issue: false hasContentIssue false
  • English
  • Français

ENUMERATION AND DIVISIBILITY OF HIGHER DIMENSIONAL KING WALKS

Part of: Algebraic combinatorics Combinatorics

Published online by Cambridge University Press:  28 July 2025

JI-CAI LIU Open the ORCID record for JI-CAI LIU [Opens in a new window]  and
YEONG-NAN YEH
JI-CAI LIU*
Affiliation:
Department of Mathematics, https://ror.org/020hxh324Wenzhou University, Wenzhou 325035, PR China
YEONG-NAN YEH
Affiliation:
Department of Mathematics, https://ror.org/020hxh324Wenzhou University, Wenzhou 325035, PR China e-mail: mayeh@wzu.edu.cn
*
e-mail: jcliu2016@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

The lattice walks in the plane starting at the origin $\mathbf {0}$ with steps in $\{-1,0,1\}^{2}\setminus \{\mathbf {0}\}$ are called king walks. We investigate enumeration and divisibility for higher dimensional king walks confined to certain regions. Specifically, we establish an explicit formula for the number of $(r+s)$-dimensional king walks of length n ending at $(a_1,\ldots ,a_r,b_1,\ldots ,b_s)$ which never dip below $x_i=0$ for 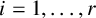$i=1,\ldots ,r$. We also derive divisibility properties for the number of $(r+s)$-dimensional king walks of length p (an odd prime) through group actions.

Keywords

king walksMotzkin numbersgroup actions

MSC classification

Primary: 05A15: Exact enumeration problems, generating functions
Secondary: 05E18: Group actions on combinatorial structures

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 12
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author was supported by the National Natural Science Foundation of China (Grant no. 12171370).

References

Amdeberhan, T., Apagodu, M. and Zeilberger, D., ‘Wilf’s “Snake Oil” method proves an identity in the Motzkin triangle’, Preprint, 2015, arXiv:1507.07660.Google Scholar
Bostan, A., Chyzak, F., van Hoeij, M., Kauers, M. and Pech, L., ‘Hypergeometric expressions for generating functions of walks with small steps in the quarter plane’, European J. Combin. 61 (2017), 242–275.10.1016/j.ejc.2016.10.010CrossRefGoogle Scholar
Bostan, A. and Kauers, M., ‘The complete generating function for Gessel walks is algebraic’, Proc. Amer. Math. Soc. 138(2010), 3063–3078; with an appendix by M. van Hoeij.10.1090/S0002-9939-2010-10398-2CrossRefGoogle Scholar
Bostan, A., Kurkova, I. and Raschel, K., ‘A human proof of Gessel’s lattice path conjecture’, Trans. Amer. Math. Soc. 369 (2017), 1365–1393.10.1090/tran/6804CrossRefGoogle Scholar
Bostan, A., Raschel, K. and Salvy, B., ‘Non- $D$ -finite excursions in the quarter plane’, J. Combin. Theory Ser. A 121 (2014), 45–63.10.1016/j.jcta.2013.09.005CrossRefGoogle Scholar
Bousquet-Mélou, M. and Mishna, M., ‘Walks with small steps in the quarter plane’, in: Algorithmic Probability and Combinatorics, Contemporary Mathematics, 520 (eds. Lladser, M. E., Maier, R. S., Mishna, M. and Rechnitzer, A.) (American Mathematical Society, Providence, RI, 2010), 1–39.Google Scholar
Dreyfus, T., Hardouin, C., Roques, J. and Singer, M. F., ‘On the nature of the generating series of walks in the quarter plane’, Invent. Math. 213 (2018), 139–203.10.1007/s00222-018-0787-zCrossRefGoogle Scholar
Gessel, I. M., ‘A probabilistic method for lattice path enumeration’, J. Statist. Plann. Inference 14 (1986), 49–58.10.1016/0378-3758(86)90009-1CrossRefGoogle Scholar
Humphreys, K., ‘A history and a survey of lattice path enumeration’, J. Statist. Plann. Inference 140 (2010), 2237–2254.10.1016/j.jspi.2010.01.020CrossRefGoogle Scholar
Kauers, M., Koutschan, C. and Zeilberger, D., ‘Proof of Ira Gessel’s lattice path conjecture’, Proc. Natl. Acad. Sci. USA 106 (2009), 11502–11505.10.1073/pnas.0901678106CrossRefGoogle Scholar
Krattenthaler, C., ‘Lattice path enumeration’, in: Handbook of Enumerative Combinatorics (ed. Bona, M.) (CRC Press, Boca Raton, FL, 2015), 589–678.Google Scholar
Kreweras, G., ‘Sur une classe de problèmes liés au treillis des partitions d’entiers’, Cahiers du B.U.R.O. 6 (1965), 5–105.Google Scholar
Kurkova, I. and Raschel, K., ‘On the functions counting walks with small steps in the quarter plane’, Publ. Math. Inst. Hautes Études Sci. 116 (2012), 69–114.10.1007/s10240-012-0045-7CrossRefGoogle Scholar
Melczer, S. and Mishna, M., ‘Singularity analysis via the iterated kernel method’, Combin. Probab. Comput. 23 (2014), 861–888.10.1017/S0963548314000145CrossRefGoogle Scholar
Melczer, S. and Wilson, M. C., ‘Higher dimensional lattice walks: connecting combinatorial and analytic behavior’, SIAM J. Discrete Math. 33 (2019), 2140–2174.10.1137/18M1220856CrossRefGoogle Scholar
Mishna, M. and Rechnitzer, A., ‘Two non-holonomic lattice walks in the quarter plane’, Theoret. Comput. Sci. 410 (2009), 3616–3630.10.1016/j.tcs.2009.04.008CrossRefGoogle Scholar
Motzkin, T., ‘Relations between hypersurface cross ratios, and a combinatorial formula for partitions of a polygon, for permanent preponderance, and for non-associative products’, Bull. Amer. Math. Soc. (N.S.) 54 (1948), 352–360.10.1090/S0002-9904-1948-09002-4CrossRefGoogle Scholar
Sloane, N. J. A., The On-Line Encyclopedia of Integer Sequences, http://oeis.org.Google Scholar
Stanley, R. P., Enumerative Combinatorics, Vol. 2 (Cambridge University Press, Cambridge, 1999).10.1017/CBO9780511609589CrossRefGoogle Scholar