Article contents
EMBEDDINGS OF FREE TOPOLOGICAL VECTOR SPACES
Published online by Cambridge University Press: 20 August 2019
Abstract
It is proved that the free topological vector space 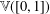 $\mathbb{V}([0,1])$ contains an isomorphic copy of the free topological vector space
$\mathbb{V}([0,1])$ contains an isomorphic copy of the free topological vector space 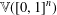 $\mathbb{V}([0,1]^{n})$ for every finite-dimensional cube
$\mathbb{V}([0,1]^{n})$ for every finite-dimensional cube 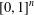 $[0,1]^{n}$, thereby answering an open question in the literature. We show that this result cannot be extended from the closed unit interval
$[0,1]^{n}$, thereby answering an open question in the literature. We show that this result cannot be extended from the closed unit interval 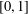 $[0,1]$ to general metrisable spaces. Indeed, we prove that the free topological vector space
$[0,1]$ to general metrisable spaces. Indeed, we prove that the free topological vector space 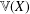 $\mathbb{V}(X)$ does not even have a vector subspace isomorphic as a topological vector space to
$\mathbb{V}(X)$ does not even have a vector subspace isomorphic as a topological vector space to 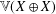 $\mathbb{V}(X\oplus X)$, where
$\mathbb{V}(X\oplus X)$, where 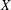 $X$ is a Cook continuum, which is a one-dimensional compact metric space. This is also shown to be the case for a rigid Bernstein set, which is a zero-dimensional subspace of the real line.
$X$ is a Cook continuum, which is a one-dimensional compact metric space. This is also shown to be the case for a rigid Bernstein set, which is a zero-dimensional subspace of the real line.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
References
- 3
- Cited by

