Published online by Cambridge University Press: 15 December 2014
Given two finitely generated groups that coarsely embed into a Hilbert space, it is known that their wreath product also embeds coarsely into a Hilbert space. We introduce a wreath product construction for general metric spaces 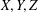 $X,Y,Z$ and derive a condition, called the (
$X,Y,Z$ and derive a condition, called the ( ${\it\delta}$-polynomial) path lifting property, such that coarse embeddability of
${\it\delta}$-polynomial) path lifting property, such that coarse embeddability of 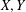 $X,Y$ and
$X,Y$ and 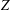 $Z$ implies coarse embeddability of
$Z$ implies coarse embeddability of 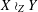 $X\wr _{Z}Y$. We also give bounds on the compression of
$X\wr _{Z}Y$. We also give bounds on the compression of 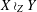 $X\wr _{Z}Y$ in terms of
$X\wr _{Z}Y$ in terms of 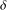 ${\it\delta}$ and the compressions of
${\it\delta}$ and the compressions of 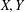 $X,Y$ and
$X,Y$ and  $Z$.
$Z$.