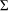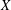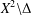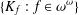Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guerrero Sánchez, David
and
Tkachuk, Vladimir V.
2016.
Domination by a Polish space of the complement of the diagonal of X implies that X is cosmic.
Topology and its Applications,
Vol. 212,
Issue. ,
p.
81.
Dow, Alan
and
Hart, Klaas Pieter
2016.
Compact spaces with a P-diagonal.
Indagationes Mathematicae,
Vol. 27,
Issue. 3,
p.
721.
Ferrando, Juan Carlos
Gabriyelyan, Saak
and
Ka̧kol, Jerzy
2019.
Bounded sets structure of CpX and quasi‐(DF)‐spaces.
Mathematische Nachrichten,
Vol. 292,
Issue. 12,
p.
2602.
Sánchez, David Guerrero
2020.
Spaces with an M-diagonal.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 114,
Issue. 1,
López-Pellicer, Manuel
2023.
Functional Analysis and Continuous Optimization.
Vol. 424,
Issue. ,
p.
1.