Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-10T23:49:13.130Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DENSE REGION IN SCATTERING DIAGRAMS

Part of: Arithmetic rings and other special rings Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  10 February 2025

TIM GRÄFNITZ Open the ORCID record for TIM GRÄFNITZ [Opens in a new window]  and
PATRICK LUO
TIM GRÄFNITZ*
Affiliation:
Institut für Algebraische Geometrie, Leibniz-Universität Hannover, Welfengarten 1, 30167 Hannover, Germany
PATRICK LUO
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WB, UK e-mail: pl485@cam.ac.uk
*
e-mail: graefnitz@math.uni-hannover.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We use deformations and mutations of scattering diagrams to show that a scattering diagram with initial functions 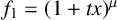$f_1=(1+tx)^\mu $ and 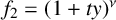$f_2=(1+ty)^\nu $ has a dense region. This answers a question asked by Gross and Pandharipande [‘Quivers, curves, and the tropical vertex’, Port. Math. 67(2) (2010), 211–259] which had been proved only for the case 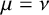$\mu =\nu $.

Keywords

scattering diagrammirror symmetrycluster algebraquiver representation

MSC classification

Primary: 14J33: Mirror symmetry
Secondary: 13F60: Cluster algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 13
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This project was financially supported by Mark Gross’ ERC Advanced Grant Mirror Symmetry in Algebraic Geometry (MSAG).

References

Argüz, H. and Gross, M., ‘The higher-dimensional tropical vertex’, Geom. Topol. 26 (2022), 2135–2235.CrossRefGoogle Scholar
Bousseau, P., ‘The quantum tropical vertex’, Geom. Topol. 24(3) (2020), 1297–1379.CrossRefGoogle Scholar
Bousseau, P., ‘Scattering diagrams, stability conditions, and coherent sheaves on ${\mathbb{P}}^2$ ’, J. Algebraic Geom. 31 (2022), 593–686.CrossRefGoogle Scholar
Bousseau, P., Brini, A. and van Garrel, M., ‘Stable maps to Looijenga pairs’, Geom. Topol. 28 (2024), 393–496.CrossRefGoogle Scholar
Bridgeland, T., ‘Scattering diagrams, Hall algebras and stability conditions’, Algebr. Geom. 4(5) (2017), 523–561.CrossRefGoogle Scholar
Gräfnitz, T., ‘Tropical correspondence for smooth del Pezzo log Calabi–Yau pairs’, J. Algebraic Geom. 31(4) (2022), 687–749.CrossRefGoogle Scholar
Gross, M., Hacking, P. and Keel, S., ‘Mirror symmetry for log Calabi–Yau surfaces I’, Publ. Math. Inst. Hautes Études Sci. 122 (2015), 65–168.CrossRefGoogle Scholar
Gross, M., Hacking, P., Keel, S. and Kontsevich, M., ‘Canonical bases for cluster algebras’, J. Amer. Math. Soc. 31(2) (2018), 497–608.CrossRefGoogle Scholar
Gross, M. and Pandharipande, R., ‘Quivers, curves, and the tropical vertex’, Port. Math. 67(2) (2010), 211–259.CrossRefGoogle Scholar
Gross, M., Pandharipande, R. and Siebert, B., ‘The tropical vertex’, Duke Math. J. 153(2) (2010), 297–362.CrossRefGoogle Scholar
Gross, M. and Siebert, B., ‘From real affine geometry to complex geometry’, Ann. of Math. (2) 174(3) (2011), 1301–1428.CrossRefGoogle Scholar
Gross, M. and Siebert, B., ‘The canonical wall structure and intrinsic mirror symmetry’, Invent. Math. 229 (2022), 1101–1202.CrossRefGoogle Scholar
Kontsevich, M. and Soibelman, Y., ‘Affine structures and non-Archimedean analytic spaces’, in: The Unity of Mathematics, Progress in Mathematics, 244 (eds. Etingof, P., Retakh, V. and Singer, I. M.) (Birkhäuser, Boston, MA, 2006), 321–385.Google Scholar
Kontsevich, M. and Soibelman, Y., ‘Stability structures, motivic Donaldson–Thomas invariants and cluster transformations’, Preprint, 2008, arXiv:0811.2435.Google Scholar
Reineke, M., ‘The Harder–Narasimhan system in quantum groups and cohomology of quiver moduli’, Invent. Math. 152 (2003), 349–368.CrossRefGoogle Scholar
Reineke, M., ‘Poisson automorphisms and quiver moduli’, J. Inst. Math. Jussieu 9(3) (2010), 653–667.CrossRefGoogle Scholar
Reineke, M., ‘Cohomology of quiver moduli, functional equations, and integrality of Donaldson–Thomas type invariants’, Compos. Math. 147(3) (2011), 943–964.CrossRefGoogle Scholar
Reineke, M. and Weist, T., ‘Refined GW/Kronecker correspondence’, Math. Ann. 355 (2013), 17–56.CrossRefGoogle Scholar