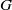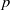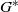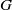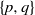Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
JIANG, QINHUI
and
SHAO, CHANGGUO
2014.
SOLVABILITY OF FINITE GROUPS WITH FOUR CONJUGACY CLASS SIZES OF CERTAIN ELEMENTS.
Bulletin of the Australian Mathematical Society,
Vol. 90,
Issue. 2,
p.
250.
KONG, QINGJUN
and
LIU, QINGFENG
2014.
‘CONJUGACY CLASS SIZE CONDITIONS WHICH IMPLY SOLVABILITY’.
Bulletin of the Australian Mathematical Society,
Vol. 89,
Issue. 3,
p.
522.