Hostname: page-component-5b777bbd6c-ks5gx Total loading time: 0 Render date: 2025-06-20T06:40:45.247Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPLEX WEIGHING MATRICES AND QUATERNARY CODES

Part of: Designs and configurations Theory of error-correcting codes and error-detecting codes

Published online by Cambridge University Press:  22 October 2024

DANNI LU Open the ORCID record for DANNI LU [Opens in a new window] ,
MINJIA SHI Open the ORCID record for MINJIA SHI [Opens in a new window] ,
RONAN EGAN Open the ORCID record for RONAN EGAN [Opens in a new window]  and
PATRICK SOLÉ Open the ORCID record for PATRICK SOLÉ [Opens in a new window]
DANNI LU
Affiliation:
Key Laboratory of Intelligent Computing and Signal Processing, Ministry of Education, School of Mathematical Sciences, Anhui University, Hefei 230601, PR China e-mail: ludanni_in@163.com
MINJIA SHI*
Affiliation:
Key Laboratory of Intelligent Computing and Signal Processing, Ministry of Education, School of Mathematical Sciences, Anhui University, Hefei 230601, PR China
RONAN EGAN
Affiliation:
School of Mathematical Sciences, Dublin City University, Dublin, Ireland e-mail: ronan.egan@dcu.ie
PATRICK SOLÉ
Affiliation:
I2M, Aix Marseille Université, CNRS, Centrale Marseille, Marseilles, France e-mail: sole@enst.fr
*
e-mail: smjwcl.good@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Weighing matrices with entries in the complex cubic and sextic roots of unity are employed to construct Hermitian self-dual codes and Hermitian linear complementary dual codes over the finite field 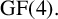$\mathrm {GF}(4).$ The parameters of these codes are explored for small matrix orders and weights.

Keywords

weighing matricesquaternary codesHermitian self-dual codesLCD codes

MSC classification

Primary: 05B20: Matrices (incidence, Hadamard, etc.)
Secondary: 94B05: Linear codes, general
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 9
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This research is supported in part by National Natural Science Foundation of China (12471490).

References

Armario, J. A. and Frau, M. D., ‘Self-dual codes from $\left(-1,1\right)$ -matrices of skew symmetric type’, Preprint, 2013, arXiv:1311.2637.Google Scholar
Assmus, E. F. and Key, J. D., Designs and their Codes (Cambridge University Press, Cambridge, 1992).CrossRefGoogle Scholar
Best, D., Kharaghani, H. and Ramp, H., ‘On unit weighing matrices with small weight’, Discrete Math. 313(7) (2013), 855–864.CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24 (1997), 235–265.CrossRefGoogle Scholar
Bruzda, W., Tadej, W. and Życzkowski, K., ‘Complex Hadamard matrices—A catalog since 2006’. https://chaos.if.uj.edu.pl// karol/hadamard/index.html.Google Scholar
Calderbank, R. A., Rains, E. M., Shor, P. W. and Sloane, N. J., ‘Quantum error correction via codes over’, IEEE Trans. Inform. Theory 44(4) (1998), 1369–1387.CrossRefGoogle Scholar
Carlet, C., Mesnager, S., Tang, C. and Qi, Y., ‘Euclidean and Hermitian LCD MDS codes’, Des. Codes Cryptogr. 86(11) (2018), 2605–2618.CrossRefGoogle Scholar
Crnković, D., Egan, R., Rodrigues, B. G. and Švob, A., ‘LCD codes from weighing matrices’, Appl. Algebra Engrg. Comm. Comput. 32(2) (2021), 175–189.CrossRefGoogle Scholar
Egan, R., ‘Generalizing pairs of complementary sequences and a construction of combinatorial structures’, Discrete Math. 343(5) (2020), Article no. 111795.CrossRefGoogle Scholar
Egan, R., ‘A survey of complex generalized weighing matrices and a construction of quantum error-correcting codes’, Discrete Math. 348(1) (2025), Article no. 114201.Google Scholar
Gaborit, P., ‘Self-dual codes’. https://www.unilim.fr/pages_perso/philippe.gaborit/SD/GF4H/GF4H.htm.Google Scholar
Harada, M., ‘New extremal ternary self-dual codes’, Australas. J. Combin. 17 (1998), 133–146.Google Scholar
Harada, M. and Munemasa, A., ‘Database of small weighing matrices’. http://www.math.is.tohoku.ac.jp/~munemasa/research/matrices/weighingmatrices.htm.Google Scholar
Li, S., Shi, M. and Liu, H., ‘Several constructions of optimal LCD codes over small finite fields’, Cryptogr. Commun. 16 (2024), 779–800.CrossRefGoogle Scholar
MacWilliams, F. J., Odlyzko, A. M., Sloane, N. J. A. and Ward, H. N., ‘Self-dual codes over GF(4)’, J. Comb. Theory Ser. A 25 (1978), 288–318.CrossRefGoogle Scholar