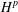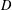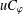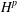Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
LO, CHING-ON
and
LOH, ANTHONY WAI-KEUNG
2022.
COMPACT AND HILBERT–SCHMIDT WEIGHTED COMPOSITION OPERATORS ON WEIGHTED BERGMAN SPACES.
Journal of the Australian Mathematical Society,
Vol. 113,
Issue. 2,
p.
208.