No CrossRef data available.
Article contents
BOUNDS ON MINORS OF BINARY MATRICES
Published online by Cambridge University Press: 23 December 2012
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We prove an upper bound on sums of squares of minors of 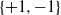 $\{+1, -1\}$-matrices. The bound is sharp for Hadamard matrices, a result due to de Launey and Levin [‘
$\{+1, -1\}$-matrices. The bound is sharp for Hadamard matrices, a result due to de Launey and Levin [‘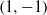 $(1,-1)$-matrices with near-extremal properties’, SIAM J. Discrete Math.23(2009), 1422–1440], but our proof is simpler. We give several corollaries relevant to minors of Hadamard matrices.
$(1,-1)$-matrices with near-extremal properties’, SIAM J. Discrete Math.23(2009), 1422–1440], but our proof is simpler. We give several corollaries relevant to minors of Hadamard matrices.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 88 , Issue 2 , October 2013 , pp. 280 - 285
- Copyright
- Copyright © 2012 Australian Mathematical Publishing Association Inc.
References
[1]Brualdi, R. A. & Schneider, H., ‘Determinantal identities: Gauss, Schur, Cauchy, Sylvester, Kronecker, Jacobi, Binet, Laplace, Muir, and Cayley’, Linear Algebra Appl. 52/53 (1983), 769–791.CrossRefGoogle Scholar
[2]de Launey, W. & Levin, D. A., ‘ $(1,-1)$-matrices with near-extremal properties’, SIAM J. Discrete Math. 23 (2009), 1422–1440.CrossRefGoogle Scholar
$(1,-1)$-matrices with near-extremal properties’, SIAM J. Discrete Math. 23 (2009), 1422–1440.CrossRefGoogle Scholar
[3]Gantmacher, F. R., The Theory of Matrices, Vol. 1 (AMS Chelsea Publishing, Providence, RI, 2000).Google Scholar
[4]Hadamard, J., ‘Résolution d’une question relative aux déterminants’, Bull. Sci. Math. 17 (1893), 240–246.Google Scholar
[5]Jacobi, C. G. J., ‘De formatione et proprietatibus determinantium’, Crelle’s J. 22 (1841), 285–318; also Gesammelte Werke, Bd. 3 (Chelsea Publishing Company, New York, 1969).Google Scholar
[6]Kahn, J., Komlós, J. & Szemerédi, E., ‘On the probability that a random  $\pm 1$-matrix is singular’, J. Amer. Math. Soc. 8 (1995), 223–240.Google Scholar
$\pm 1$-matrix is singular’, J. Amer. Math. Soc. 8 (1995), 223–240.Google Scholar
[7]Koukouvinos, C., Lappas, E., Mitrouli, M. & Seberry, J., ‘An algorithm to find formulae and values of minors for Hadamard matrices: II’, Linear Algebra Appl. 371 (2003), 111–124.CrossRefGoogle Scholar
[8]Koukouvinos, C., Mitrouli, M. & Seberry, J., ‘An algorithm to find formulae and values of minors for Hadamard matrices’, Linear Algebra Appl. 330 (2001), 129–147.CrossRefGoogle Scholar
[9]Little, C. H. C. & Thuente, D. J., ‘The Hadamard conjecture and circuits of length four in a complete bipartite graph’, J. Aust. Math. Soc. (Ser. A) 31 (1981), 252–256.CrossRefGoogle Scholar
[11]OEIS Foundation Inc., ‘The on-line encyclopedia of integer sequences’, 2012,http://oeis.org/A057982. Also A046747.Google Scholar
[12]Sharpe, F. R., ‘The maximum value of a determinant’, Bull. Amer. Math. Soc. 14 (1907), 121–123.CrossRefGoogle Scholar
[13]Szöllősi, F., ‘Exotic complex Hadamard matrices and their equivalence’, Cryptogr. Commun. 2 (2010), 187–198.CrossRefGoogle Scholar
[14]Tao, T. & Vu, V., ‘On random  $\pm 1$ matrices: singularity and determinant’, Random Structures Algorithms 28 (2006), 1–23.CrossRefGoogle Scholar
$\pm 1$ matrices: singularity and determinant’, Random Structures Algorithms 28 (2006), 1–23.CrossRefGoogle Scholar
[15]Turán, P., ‘On extremal problems concerning determinants’, Math. Naturwiss. Anz. Ungar. Akad. Wiss. 59 (1940), 95–105.Google Scholar

