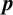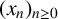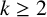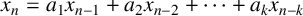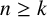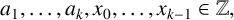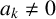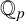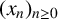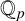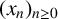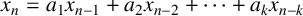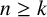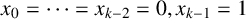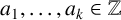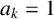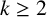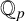1 Introduction and statement of results
For a set of integers A, the set
![]() $R(A)=\{a/b:a,b\in A, b\neq 0\}$
is called the ratio set or quotient set of A. Several authors have studied the denseness of ratio sets of different subsets of
$R(A)=\{a/b:a,b\in A, b\neq 0\}$
is called the ratio set or quotient set of A. Several authors have studied the denseness of ratio sets of different subsets of
![]() $\mathbb {N}$
in the positive real numbers (see [Reference Brown, Dairyko, Garcia, Lutz and Someck3, Reference Bukor and Csiba5–Reference Bukor and Tóth7, Reference Garcia, Poore, Selhorst-Jones and Simon15, Reference Hedman and Rose16–Reference Mišík20, Reference Šalát24, Reference Šalát25, Reference Starni29, Reference Strauch and Tóth30]). An analogous study has also been done for algebraic number fields (see [Reference Garcia12, Reference Sittinger28]).
$\mathbb {N}$
in the positive real numbers (see [Reference Brown, Dairyko, Garcia, Lutz and Someck3, Reference Bukor and Csiba5–Reference Bukor and Tóth7, Reference Garcia, Poore, Selhorst-Jones and Simon15, Reference Hedman and Rose16–Reference Mišík20, Reference Šalát24, Reference Šalát25, Reference Starni29, Reference Strauch and Tóth30]). An analogous study has also been done for algebraic number fields (see [Reference Garcia12, Reference Sittinger28]).
For a prime p, let
![]() $\mathbb {Q}_p$
denote the field of p-adic numbers. The denseness of ratio sets in
$\mathbb {Q}_p$
denote the field of p-adic numbers. The denseness of ratio sets in
![]() $\mathbb {Q}_p$
has been studied by several authors (see [Reference Antony and Barman1, Reference Antony, Barman and Miska2, Reference Donnay, Garcia and Rouse10, Reference Garcia, Hong, Luca, Pinsker, Sanna, Schechter and Starr13, Reference Garcia and Luca14, Reference Miska21–Reference Miska and Sanna23, Reference Sanna27]). Let
$\mathbb {Q}_p$
has been studied by several authors (see [Reference Antony and Barman1, Reference Antony, Barman and Miska2, Reference Donnay, Garcia and Rouse10, Reference Garcia, Hong, Luca, Pinsker, Sanna, Schechter and Starr13, Reference Garcia and Luca14, Reference Miska21–Reference Miska and Sanna23, Reference Sanna27]). Let
![]() $(F_n)_{n\geq 0}$
be the sequence of Fibonacci numbers, defined by
$(F_n)_{n\geq 0}$
be the sequence of Fibonacci numbers, defined by
![]() $F_0=0$
,
$F_0=0$
,
![]() $F_1=1$
and
$F_1=1$
and
![]() $F_n=F_{n-1}+F_{n-2}$
for all integers
$F_n=F_{n-1}+F_{n-2}$
for all integers
![]() $n\geq 2$
. In [Reference Garcia and Luca14], Garcia and Luca showed that the ratio set of Fibonacci numbers is dense in
$n\geq 2$
. In [Reference Garcia and Luca14], Garcia and Luca showed that the ratio set of Fibonacci numbers is dense in
![]() $\mathbb {Q}_p$
for all primes p. Later, Sanna [Reference Sanna27, Theorem 1.2] showed that, for any
$\mathbb {Q}_p$
for all primes p. Later, Sanna [Reference Sanna27, Theorem 1.2] showed that, for any
![]() $k\geq 2$
and any prime p, the ratio set of the k-generalised Fibonacci numbers is dense in
$k\geq 2$
and any prime p, the ratio set of the k-generalised Fibonacci numbers is dense in
![]() $\mathbb {Q}_p$
. Sanna remarked that his result could be extended to other linear recurrences over the integers. However, he used some specific properties of the k-generalised Fibonacci numbers in the proof. Therefore, he asked the following question.
$\mathbb {Q}_p$
. Sanna remarked that his result could be extended to other linear recurrences over the integers. However, he used some specific properties of the k-generalised Fibonacci numbers in the proof. Therefore, he asked the following question.
Question 1.1 [Reference Sanna27, Question 1.3].
Let
![]() $(S_n)_{n\geq 0}$
be a linear recurrence of order
$(S_n)_{n\geq 0}$
be a linear recurrence of order
![]() $k\geq 2$
satisfying
$k\geq 2$
satisfying
![]() $S_n=a_1S_{n-1}+a_2S_{n-2}+\cdots +a_kS_{n-k}$
for all integers
$S_n=a_1S_{n-1}+a_2S_{n-2}+\cdots +a_kS_{n-k}$
for all integers
![]() $n\geq k$
, where
$n\geq k$
, where
![]() $a_1,\ldots ,a_k,S_0,\ldots ,S_{k-1}\in \mathbb {Z},$
with
$a_1,\ldots ,a_k,S_0,\ldots ,S_{k-1}\in \mathbb {Z},$
with
![]() $a_k\neq 0.$
For which prime numbers p is the quotient set of
$a_k\neq 0.$
For which prime numbers p is the quotient set of
![]() $(S_n)_{n\geq 0}$
dense in
$(S_n)_{n\geq 0}$
dense in
![]() $\mathbb {Q}_p?$
$\mathbb {Q}_p?$
In [Reference Garcia, Hong, Luca, Pinsker, Sanna, Schechter and Starr13], Garcia et al. studied the quotient sets of certain second-order recurrences: given two fixed integers r and s, let
![]() $(a_n)_{n\geq 0}$
be defined by
$(a_n)_{n\geq 0}$
be defined by
![]() $a_{n}=ra_{n-1}+sa_{n-2}$
for
$a_{n}=ra_{n-1}+sa_{n-2}$
for
![]() $n\geq 2$
with initial values
$n\geq 2$
with initial values
![]() $a_0=0$
and
$a_0=0$
and
![]() $a_1=1$
, and let
$a_1=1$
, and let
![]() $(b_n)_{n\geq 0}$
be defined by
$(b_n)_{n\geq 0}$
be defined by
![]() $b_{n}=rb_{n-1}+sb_{n-2}$
for
$b_{n}=rb_{n-1}+sb_{n-2}$
for
![]() $n\geq 2$
with initial values
$n\geq 2$
with initial values
![]() $b_0=2$
and
$b_0=2$
and
![]() $b_1=r$
.
$b_1=r$
.
Theorem 1.2 [Reference Garcia, Hong, Luca, Pinsker, Sanna, Schechter and Starr13, Theorem 5.2].
With the notation as above, let
![]() $A=\{a_n: n\geq 0\}$
and
$A=\{a_n: n\geq 0\}$
and
![]() $B=\{b_n: n\geq 0\}$
.
$B=\{b_n: n\geq 0\}$
.
-
(a) If
 $p\mid s$
and
$p\mid s$
and
 $p\nmid r$
, then
$p\nmid r$
, then
 $R(A)$
is not dense in
$R(A)$
is not dense in
 $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
. -
(b) If
 $p\nmid s$
, then
$p\nmid s$
, then
 $R(A)$
is dense in
$R(A)$
is dense in
 $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
. -
(c) For all odd primes p,
 $R(B)$
is dense in
$R(B)$
is dense in
 $\mathbb {Q}_p$
if and only if there exists a positive integer n such that
$\mathbb {Q}_p$
if and only if there exists a positive integer n such that
 $p\mid b_n$
.
$p\mid b_n$
.
We study ratio sets of some other linear recurrences over the set of integers. Our results give some answers to Question 1.1. Our first result gives a sufficient condition for the denseness of the ratio sets of certain kth-order recurrence sequences. Finding a general solution to Question 1.1 seems to be a difficult problem. Hence, in Theorem 1.3, we consider kth-order recurrence sequences for which
![]() $a_k=1$
and with initial values
$a_k=1$
and with initial values
![]() $x_0=\cdots =x_{k-2}=0$
,
$x_0=\cdots =x_{k-2}=0$
,
![]() $x_{k-1}=1$
. Recall that a Pisot number is a positive algebraic integer greater than
$x_{k-1}=1$
. Recall that a Pisot number is a positive algebraic integer greater than
![]() $1$
all of whose conjugate elements have absolute value less than
$1$
all of whose conjugate elements have absolute value less than
![]() $1$
.
$1$
.
Theorem 1.3. Let
![]() $(x_n)_{n\geq 0}$
be a
$(x_n)_{n\geq 0}$
be a
![]() $kth$
-order linear recurrence satisfying
$kth$
-order linear recurrence satisfying
for all integers
![]() $n\geq k$
with initial values
$n\geq k$
with initial values
![]() $x_0=x_1=\cdots =x_{k-2}=0, x_{k-1}=1$
and
$x_0=x_1=\cdots =x_{k-2}=0, x_{k-1}=1$
and
![]() $a_1,\ldots ,a_{k-1}\in \mathbb {Z}$
. Suppose that the characteristic polynomial of the recurrence sequence has a root
$a_1,\ldots ,a_{k-1}\in \mathbb {Z}$
. Suppose that the characteristic polynomial of the recurrence sequence has a root
![]() $\pm \alpha $
, where
$\pm \alpha $
, where
![]() $\alpha $
is a Pisot number. If p is a prime such that the characteristic polynomial of the recurrence sequence is irreducible in
$\alpha $
is a Pisot number. If p is a prime such that the characteristic polynomial of the recurrence sequence is irreducible in
![]() $\mathbb {Q}_p$
, then the quotient set of
$\mathbb {Q}_p$
, then the quotient set of
![]() $(x_n)_{n\geq 0}$
is dense in
$(x_n)_{n\geq 0}$
is dense in
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
If we take
![]() $k=3$
in Theorem 1.3, then we have the following corollary.
$k=3$
in Theorem 1.3, then we have the following corollary.
Corollary 1.4. Let
![]() $(x_n)_{n\geq 0}$
be a third-order linear recurrence satisfying
$(x_n)_{n\geq 0}$
be a third-order linear recurrence satisfying
for all integers
![]() $n\geq 3$
with initial values
$n\geq 3$
with initial values
![]() $x_0=x_1=0, x_2=1$
, where the integers a and b are such that
$x_0=x_1=0, x_2=1$
, where the integers a and b are such that
![]() $(a+b)(b-a-2)<0$
. If p is a prime such that the characteristic polynomial of the recurrence sequence is irreducible in
$(a+b)(b-a-2)<0$
. If p is a prime such that the characteristic polynomial of the recurrence sequence is irreducible in
![]() $\mathbb {Q}_p$
, then the quotient set of
$\mathbb {Q}_p$
, then the quotient set of
![]() $(x_n)_{n\geq 0}$
is dense in
$(x_n)_{n\geq 0}$
is dense in
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
We discuss two examples as applications of Corollary 1.4.
Example 1.5. For
![]() $a\in \mathbb {N}$
, let
$a\in \mathbb {N}$
, let
![]() $\ell $
be an odd positive integer less than
$\ell $
be an odd positive integer less than
![]() $2a$
. Let
$2a$
. Let
![]() $(x_n)_{n\geq 0}$
be a linear recurrence satisfying
$(x_n)_{n\geq 0}$
be a linear recurrence satisfying
![]() $x_{n}=ax_{n-1}+(a-\ell )x_{n-2}+x_{n-3}$
for all integers
$x_{n}=ax_{n-1}+(a-\ell )x_{n-2}+x_{n-3}$
for all integers
![]() $n\geq 3$
with initial values
$n\geq 3$
with initial values
![]() $x_0=x_1=0, x_2=1$
. Then a and
$x_0=x_1=0, x_2=1$
. Then a and
![]() $b:=a-\ell $
satisfy
$b:=a-\ell $
satisfy
![]() $(a+b)(b-a-2) <0$
. The characteristic polynomial
$(a+b)(b-a-2) <0$
. The characteristic polynomial
![]() $p(x)=x^3-ax^2-(a-\ell )x-1$
is irreducible in
$p(x)=x^3-ax^2-(a-\ell )x-1$
is irreducible in
![]() $\mathbb {Q}_2$
because
$\mathbb {Q}_2$
because
![]() $p(0)\neq 0$
and
$p(0)\neq 0$
and
![]() $p(1)=-2a+\ell \not \equiv 0\pmod {2}$
. Therefore, by Theorem 1.3,
$p(1)=-2a+\ell \not \equiv 0\pmod {2}$
. Therefore, by Theorem 1.3,
![]() $R((x_n)_{n\geq 0})$
is dense in
$R((x_n)_{n\geq 0})$
is dense in
![]() $\mathbb {Q}_2$
.
$\mathbb {Q}_2$
.
Example 1.6. For
![]() $a\in \mathbb {N}$
such that
$a\in \mathbb {N}$
such that
![]() $3\nmid a$
, let
$3\nmid a$
, let
![]() $\ell $
be an odd positive integer less than
$\ell $
be an odd positive integer less than
![]() $2a$
and such that
$2a$
and such that
![]() $3\mid \ell $
. Let
$3\mid \ell $
. Let
![]() $(x_n)_{n\geq 0}$
be a linear recurrence satisfying
$(x_n)_{n\geq 0}$
be a linear recurrence satisfying
![]() $x_{n}=ax_{n-1}+(a-\ell )x_{n-2}+ x_{n-3}$
for all integers
$x_{n}=ax_{n-1}+(a-\ell )x_{n-2}+ x_{n-3}$
for all integers
![]() $n\geq 3$
with initial values
$n\geq 3$
with initial values
![]() $x_0=x_1=0, x_2=1$
. Then a and
$x_0=x_1=0, x_2=1$
. Then a and
![]() $b=a-\ell $
satisfy
$b=a-\ell $
satisfy
![]() $(a+b)(b-a-2)<0$
. The characteristic polynomial
$(a+b)(b-a-2)<0$
. The characteristic polynomial
![]() $p(x)=x^3-ax^2-(a-\ell ) x-1$
is irreducible in
$p(x)=x^3-ax^2-(a-\ell ) x-1$
is irreducible in
![]() $\mathbb {Q}_3$
because
$\mathbb {Q}_3$
because
![]() $p(0)\neq 0$
,
$p(0)\neq 0$
,
![]() $p(1)=-2a+\ell \not \equiv 0\pmod {3}$
and
$p(1)=-2a+\ell \not \equiv 0\pmod {3}$
and
![]() $p(2)=-6a+2\ell +7\not \equiv 0\pmod {3}$
. Therefore, by Theorem 1.3,
$p(2)=-6a+2\ell +7\not \equiv 0\pmod {3}$
. Therefore, by Theorem 1.3,
![]() $R((x_n)_{n\geq 0})$
is dense in
$R((x_n)_{n\geq 0})$
is dense in
![]() $\mathbb {Q}_3$
.
$\mathbb {Q}_3$
.
Next, we consider recurrence sequences whose nth term depends on all the previous
![]() $n-1$
terms and obtain the following results.
$n-1$
terms and obtain the following results.
Theorem 1.7. Let
![]() $(x_n)_{n\geq 0}$
be a linear recurrence satisfying
$(x_n)_{n\geq 0}$
be a linear recurrence satisfying
for all integers
![]() $n\geq 1$
with initial value
$n\geq 1$
with initial value
![]() $x_0=1$
. Then the quotient set of
$x_0=1$
. Then the quotient set of
![]() $(x_n)_{n\geq 0}$
is dense in
$(x_n)_{n\geq 0}$
is dense in
![]() $\mathbb {Q}_p$
for all primes p.
$\mathbb {Q}_p$
for all primes p.
The recurrence relation given in Theorem 1.7 generates a subsequence of the Fibonacci sequence.
Theorem 1.8. Let
![]() $(x_n)_{n\geq 0}$
be a linear recurrence satisfying
$(x_n)_{n\geq 0}$
be a linear recurrence satisfying
for all integers
![]() $n\geq 1$
, with
$n\geq 1$
, with
![]() $x_0, a,r\in \mathbb {Z}$
. Then the quotient set of
$x_0, a,r\in \mathbb {Z}$
. Then the quotient set of
![]() $(x_n)_{n\geq 0}$
is not dense in
$(x_n)_{n\geq 0}$
is not dense in
![]() $\mathbb {Q}_p$
for all primes p.
$\mathbb {Q}_p$
for all primes p.
In Theorem 1.2, Garcia et al. studied second-order recurrence relations with specific initial values. In the following result, we consider a particular second-order recurrence sequence with arbitrary initial values
![]() $x_0$
and
$x_0$
and
![]() $x_1$
in the set of integers.
$x_1$
in the set of integers.
Theorem 1.9. Let
![]() $(x_n)_{n\geq 0}$
be a second-order linear recurrence satisfying
$(x_n)_{n\geq 0}$
be a second-order linear recurrence satisfying
![]() $x_{n}=2ax_{n-1}-a^2x_{n-2}$
for all integers
$x_{n}=2ax_{n-1}-a^2x_{n-2}$
for all integers
![]() $n\geq 2$
, where
$n\geq 2$
, where
![]() $a,x_0,x_1\in \mathbb {Z}$
. Then the quotient set of
$a,x_0,x_1\in \mathbb {Z}$
. Then the quotient set of
![]() $(x_n)_{n\geq 0}$
is dense in
$(x_n)_{n\geq 0}$
is dense in
![]() $\mathbb {Q}_p$
for all primes p satisfying
$\mathbb {Q}_p$
for all primes p satisfying
![]() $p\nmid a(x_1-ax_0)$
.
$p\nmid a(x_1-ax_0)$
.
For a prime p, let
![]() $\nu _p$
denote the p-adic valuation. The following theorem gives a set of linear recurrence sequences of order k whose ratio sets are not dense in
$\nu _p$
denote the p-adic valuation. The following theorem gives a set of linear recurrence sequences of order k whose ratio sets are not dense in
![]() $\mathbb {Q}_p.$
$\mathbb {Q}_p.$
Theorem 1.10. Let
![]() $(x_n)_{n\geq 0}$
be a linear recurrence of order
$(x_n)_{n\geq 0}$
be a linear recurrence of order
![]() $k\geq 2$
satisfying
$k\geq 2$
satisfying
for all integers
![]() $n\geq k$
, where
$n\geq k$
, where
![]() $x_0,\ldots ,x_{k-1}, a_1,\ldots ,a_k\in \mathbb {Z}$
. If p is a prime such that
$x_0,\ldots ,x_{k-1}, a_1,\ldots ,a_k\in \mathbb {Z}$
. If p is a prime such that
![]() $p\nmid a_k$
and
$p\nmid a_k$
and
![]() $\min \{\nu _p(a_j):1\leq j<k\}>\max \{\nu _p(x_m)-\nu _p(x_n):0\leq m,n<k\}$
, then the quotient set of
$\min \{\nu _p(a_j):1\leq j<k\}>\max \{\nu _p(x_m)-\nu _p(x_n):0\leq m,n<k\}$
, then the quotient set of
![]() $(x_n)_{n\geq 0}$
is not dense in
$(x_n)_{n\geq 0}$
is not dense in
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
The next example is an application of Theorem 1.10. Given a prime p, this example gives infinitely many recurrence sequences of order
![]() $k\geq 2$
whose quotient sets are not dense in
$k\geq 2$
whose quotient sets are not dense in
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
Example 1.11. Let
![]() $(x_n)_{n\geq 0}$
be a linear recurrence of order
$(x_n)_{n\geq 0}$
be a linear recurrence of order
![]() $k\geq 2$
satisfying
$k\geq 2$
satisfying
for all integers
![]() $n\geq k$
, where
$n\geq k$
, where
![]() $x_0=x_1=\cdots =x_{k-1}=1$
and
$x_0=x_1=\cdots =x_{k-1}=1$
and
![]() $a_1,\ldots ,a_k\in \mathbb {Z}$
. If p is a prime such that
$a_1,\ldots ,a_k\in \mathbb {Z}$
. If p is a prime such that
![]() $p\mid a_j,1\leq j\leq k-1$
, and
$p\mid a_j,1\leq j\leq k-1$
, and
![]() $p\nmid a_k$
, then by Theorem 1.10, the quotient set of
$p\nmid a_k$
, then by Theorem 1.10, the quotient set of
![]() $(x_n)_{n\geq 0}$
is not dense in
$(x_n)_{n\geq 0}$
is not dense in
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
2 Preliminaries
Let p be a prime and r be a nonzero rational number. Then r has a unique representation of the form
![]() $r= \pm p^k a/b$
, where
$r= \pm p^k a/b$
, where
![]() $k\in \mathbb {Z}, a, b \in \mathbb {N}$
and
$k\in \mathbb {Z}, a, b \in \mathbb {N}$
and
![]() $\gcd (a,p)= \gcd (p,b)=\gcd (a,b)=1$
. The p-adic valuation of r is
$\gcd (a,p)= \gcd (p,b)=\gcd (a,b)=1$
. The p-adic valuation of r is
![]() $\nu _p(r)=k$
and its p-adic absolute value is
$\nu _p(r)=k$
and its p-adic absolute value is
![]() $\|r\|_p=p^{-k}$
. By convention,
$\|r\|_p=p^{-k}$
. By convention,
![]() $\nu _p(0)=\infty $
and
$\nu _p(0)=\infty $
and
![]() $\|0\|_p=0$
. The p-adic metric on
$\|0\|_p=0$
. The p-adic metric on
![]() $\mathbb {Q}$
is
$\mathbb {Q}$
is
![]() $d(x,y)=\|x-y\|_p$
. The field
$d(x,y)=\|x-y\|_p$
. The field
![]() $\mathbb {Q}_p$
of p-adic numbers is the completion of
$\mathbb {Q}_p$
of p-adic numbers is the completion of
![]() $\mathbb {Q}$
with respect to the p-adic metric. The p-adic absolute value can be extended to a finite normal extension field K over
$\mathbb {Q}$
with respect to the p-adic metric. The p-adic absolute value can be extended to a finite normal extension field K over
![]() $\mathbb {Q}_p$
of degree n. For
$\mathbb {Q}_p$
of degree n. For
![]() $\alpha \in K$
, define
$\alpha \in K$
, define
![]() $\|\alpha \|_p$
as the nth root of the determinant of the matrix of the linear transformation from the vector space K over
$\|\alpha \|_p$
as the nth root of the determinant of the matrix of the linear transformation from the vector space K over
![]() $\mathbb {Q}_p$
to itself defined by
$\mathbb {Q}_p$
to itself defined by
![]() $x\mapsto \alpha x$
for all
$x\mapsto \alpha x$
for all
![]() $x\in K$
. Also, define
$x\in K$
. Also, define
![]() $\nu _p(\alpha )$
as the unique rational number satisfying
$\nu _p(\alpha )$
as the unique rational number satisfying
![]() $\|\alpha \|_p=p^{-\nu _p(\alpha )}$
.
$\|\alpha \|_p=p^{-\nu _p(\alpha )}$
.
The following results will be used in the proofs of our theorems.
Lemma 2.1 [Reference Garcia, Hong, Luca, Pinsker, Sanna, Schechter and Starr13, Lemma 2.1].
If S is dense in
![]() $\mathbb {Q}_p$
, then for each finite value of the p-adic valuation, there is an element of S with that valuation.
$\mathbb {Q}_p$
, then for each finite value of the p-adic valuation, there is an element of S with that valuation.
Lemma 2.2 [Reference Garcia, Hong, Luca, Pinsker, Sanna, Schechter and Starr13, Lemma 2.3].
Let
![]() $A\subset \mathbb {N}$
.
$A\subset \mathbb {N}$
.
-
(1) If A is p-adically dense in
 $\mathbb {N}$
, then
$\mathbb {N}$
, then
 $R(A)$
is dense in
$R(A)$
is dense in
 $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
. -
(2) If
 $R(A)$
is p-adically dense in
$R(A)$
is p-adically dense in
 $\mathbb {N}$
, then
$\mathbb {N}$
, then
 $R(A)$
is dense in
$R(A)$
is dense in
 $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
Theorem 2.3 [Reference Brumer4, Theorem 1].
Let
![]() $\alpha _1,\ldots ,\alpha _n$
be units in
$\alpha _1,\ldots ,\alpha _n$
be units in
![]() $\Omega _p$
, the completion of the algebraic closure of
$\Omega _p$
, the completion of the algebraic closure of
![]() $\mathbb {Q}_p,$
which are algebraic over the rationals
$\mathbb {Q}_p,$
which are algebraic over the rationals
![]() $\mathbb {Q}$
and whose p-adic logarithms are linearly independent over
$\mathbb {Q}$
and whose p-adic logarithms are linearly independent over
![]() $\mathbb {Q}$
. These logarithms are then linearly independent over the algebraic closure of
$\mathbb {Q}$
. These logarithms are then linearly independent over the algebraic closure of
![]() $\mathbb {Q}$
in
$\mathbb {Q}$
in
![]() $\Omega _p$
.
$\Omega _p$
.
3 Proof of the theorems
Proof of Theorem 1.3.
Let
![]() $p(x)=x^k-a_1x^{k-1}-a_2x^{k-2}-\cdots -a_{k-1}x-1$
be the characteristic polynomial of the recurrence. Let
$p(x)=x^k-a_1x^{k-1}-a_2x^{k-2}-\cdots -a_{k-1}x-1$
be the characteristic polynomial of the recurrence. Let
![]() $\alpha _1,\ldots ,\alpha _{k}$
be the k distinct roots of the characteristic polynomial in its splitting field, say, K over
$\alpha _1,\ldots ,\alpha _{k}$
be the k distinct roots of the characteristic polynomial in its splitting field, say, K over
![]() $\mathbb {Q}_p$
. The generating function of the sequence is
$\mathbb {Q}_p$
. The generating function of the sequence is
 $$ \begin{align*} t(x)=\frac{x^{k-1}}{1-a_1x-a_2x^2-\cdots-x^k}=\sum_{i=1}^k\frac{1}{q(\alpha_i)}\sum_{n=0}^{\infty}\alpha_i^nx^n, \end{align*} $$
$$ \begin{align*} t(x)=\frac{x^{k-1}}{1-a_1x-a_2x^2-\cdots-x^k}=\sum_{i=1}^k\frac{1}{q(\alpha_i)}\sum_{n=0}^{\infty}\alpha_i^nx^n, \end{align*} $$
where
![]() $q(x):=p'(x)$
, the derivative of the polynomial
$q(x):=p'(x)$
, the derivative of the polynomial
![]() $p(x)$
. Hence, the nth term of the sequence is given by
$p(x)$
. Hence, the nth term of the sequence is given by
 $$ \begin{align*} x_n=\sum_{i=1}^{k}\frac{1}{q(\alpha_i)}\alpha_i^n,\quad n\geq0. \end{align*} $$
$$ \begin{align*} x_n=\sum_{i=1}^{k}\frac{1}{q(\alpha_i)}\alpha_i^n,\quad n\geq0. \end{align*} $$
Since
![]() $p(0)=-1$
, the roots of
$p(0)=-1$
, the roots of
![]() $p(x)$
are units in the ring formed by elements in K with p-adic absolute value less than or equal to
$p(x)$
are units in the ring formed by elements in K with p-adic absolute value less than or equal to
![]() $1$
. Following Sanna’s proof of [Reference Sanna27, Theorem 1.2], we can choose an even
$1$
. Following Sanna’s proof of [Reference Sanna27, Theorem 1.2], we can choose an even
![]() $t\in \mathbb {N}$
such that the function
$t\in \mathbb {N}$
such that the function
 $$ \begin{align*} G(z):=\sum_{i=1}^{k}\frac{1}{q(\alpha_i)}\exp_p(z\log_p(\alpha_i^t)) \end{align*} $$
$$ \begin{align*} G(z):=\sum_{i=1}^{k}\frac{1}{q(\alpha_i)}\exp_p(z\log_p(\alpha_i^t)) \end{align*} $$
is analytic over
![]() $\mathbb {Z}_p$
and the Taylor series of
$\mathbb {Z}_p$
and the Taylor series of
![]() $G(z)$
around
$G(z)$
around
![]() $0$
converges for all
$0$
converges for all
![]() $z\in \mathbb {Z}_p$
. Also, note that
$z\in \mathbb {Z}_p$
. Also, note that
![]() $x_{nt}=G(n)$
for
$x_{nt}=G(n)$
for
![]() $n\geq 0$
.
$n\geq 0$
.
We now use a variant of the following lemma which gives the multiplicative independence of any
![]() $k-1$
roots among the k roots
$k-1$
roots among the k roots
![]() $\alpha _1,\ldots ,\alpha _k$
of the characteristic polynomial
$\alpha _1,\ldots ,\alpha _k$
of the characteristic polynomial
![]() $x^k-x^{k-1}-\cdots -x-1$
of the k-generalised Fibonacci sequence in the field of complex numbers.
$x^k-x^{k-1}-\cdots -x-1$
of the k-generalised Fibonacci sequence in the field of complex numbers.
Lemma 3.1 [Reference Fuchs, Hutle, Luca and Szalay11, Lemma 1].
With the notation above, each set of
![]() $k-1$
different roots
$k-1$
different roots
![]() $\alpha _1,\ldots ,\alpha _{k-1}$
is multiplicatively independent, that is,
$\alpha _1,\ldots ,\alpha _{k-1}$
is multiplicatively independent, that is,
![]() $\alpha _1^{e_1}\cdots \alpha _{k-1}^{e_{k-1}}=1$
for some integers
$\alpha _1^{e_1}\cdots \alpha _{k-1}^{e_{k-1}}=1$
for some integers
![]() $e_1,\ldots ,e_{k-1}$
if and only if
$e_1,\ldots ,e_{k-1}$
if and only if
![]() $e_1=\cdots =e_{k-1}=0$
.
$e_1=\cdots =e_{k-1}=0$
.
Let
![]() $\sigma(\alpha_1) = \pm \alpha$
, where
$\sigma(\alpha_1) = \pm \alpha$
, where
![]() $\alpha$
is a Pisot number with absolute value greater than 1, the other roots,
$\alpha$
is a Pisot number with absolute value greater than 1, the other roots,
![]() $\sigma (\alpha _2),\ldots ,\sigma (\alpha _k)$
, having absolute values less than
$\sigma (\alpha _2),\ldots ,\sigma (\alpha _k)$
, having absolute values less than
![]() $1$
, where
$1$
, where
![]() $\sigma $
is an isomorphism from
$\sigma $
is an isomorphism from
![]() $\mathbb {Q}(\alpha _1,\ldots ,\alpha _k)$
to the splitting field of
$\mathbb {Q}(\alpha _1,\ldots ,\alpha _k)$
to the splitting field of
![]() $p(x)$
over
$p(x)$
over
![]() $\mathbb {Q}$
in the field of complex numbers. Therefore, the proof of Lemma 3.1 holds true for the roots of
$\mathbb {Q}$
in the field of complex numbers. Therefore, the proof of Lemma 3.1 holds true for the roots of
![]() $p(x)$
, which are
$p(x)$
, which are
![]() $\sigma (\alpha _1),\ldots , \sigma (\alpha _k)$
, since
$\sigma (\alpha _1),\ldots , \sigma (\alpha _k)$
, since
![]() $\log |\sigma (\alpha _1)|$
is positive and
$\log |\sigma (\alpha _1)|$
is positive and
![]() $\log |\sigma (\alpha _2)|,\ldots ,\log |\sigma (\alpha _k)|$
are negative. Hence,
$\log |\sigma (\alpha _2)|,\ldots ,\log |\sigma (\alpha _k)|$
are negative. Hence,
![]() $\sigma (\alpha _1),\ldots ,\sigma (\alpha _{k-1}$
) are multiplicatively independent, implying that
$\sigma (\alpha _1),\ldots ,\sigma (\alpha _{k-1}$
) are multiplicatively independent, implying that
![]() $\alpha _1^t,\ldots , \alpha _{k-1}^t$
are multiplicatively independent. Thus,
$\alpha _1^t,\ldots , \alpha _{k-1}^t$
are multiplicatively independent. Thus,
![]() $\log _p(\alpha _1^t),\ldots ,\log _p(\alpha _{k-1}^t)$
are linearly independent over
$\log _p(\alpha _1^t),\ldots ,\log _p(\alpha _{k-1}^t)$
are linearly independent over
![]() $\mathbb {Z}$
and hence linearly independent over the algebraic numbers by Theorem 2.3.
$\mathbb {Z}$
and hence linearly independent over the algebraic numbers by Theorem 2.3.
Suppose
![]() $G'(0)=\sum _{i=0}^{k}({1}/{q(\alpha _i)})\log _p(\alpha _i^t)=0$
. Since
$G'(0)=\sum _{i=0}^{k}({1}/{q(\alpha _i)})\log _p(\alpha _i^t)=0$
. Since
![]() $\log _p(\alpha _k^t)=-\log _p(\alpha _1^t)-\cdots -\log _p(\alpha _k^t)$
as the product of the roots is
$\log _p(\alpha _k^t)=-\log _p(\alpha _1^t)-\cdots -\log _p(\alpha _k^t)$
as the product of the roots is
![]() $-1$
and t is even, we obtain
$-1$
and t is even, we obtain
 $$ \begin{align*} \sum_{i=1}^{k-1} \bigg(\frac{1}{q(\alpha_i)}-\frac{1}{q(\alpha_k)}\bigg)\log_p(\alpha_i^t)=0. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{k-1} \bigg(\frac{1}{q(\alpha_i)}-\frac{1}{q(\alpha_k)}\bigg)\log_p(\alpha_i^t)=0. \end{align*} $$
By linear independence of
![]() $\log _p(\alpha _1^t),\ldots ,\log _p(\alpha _{k-1}^t)$
, we have
$\log _p(\alpha _1^t),\ldots ,\log _p(\alpha _{k-1}^t)$
, we have
![]() ${1}/{q(\alpha _1)}=\cdots = {1}/{q(\alpha _k)}=c$
, for some p-adic number c. This gives k distinct roots
${1}/{q(\alpha _1)}=\cdots = {1}/{q(\alpha _k)}=c$
, for some p-adic number c. This gives k distinct roots
![]() $\alpha _1,\ldots ,\alpha _k$
of the (
$\alpha _1,\ldots ,\alpha _k$
of the (
![]() $k-1$
)-degree polynomial
$k-1$
)-degree polynomial
![]() $q(x)-{1}/{c}$
, which is not possible.Therefore,
$q(x)-{1}/{c}$
, which is not possible.Therefore,
![]() $G'(0)\neq 0$
. Since
$G'(0)\neq 0$
. Since
 $$ \begin{align*} G(z)=\sum_{j=0}^\infty\frac{G^{(\,j)}(0)}{j!}z^{\,j} \end{align*} $$
$$ \begin{align*} G(z)=\sum_{j=0}^\infty\frac{G^{(\,j)}(0)}{j!}z^{\,j} \end{align*} $$
converges at
![]() $z=1$
, it follows that
$z=1$
, it follows that
![]() $\|{G^{(\,j)}(0)}/{j!}\|_p\rightarrow 0$
. Hence, there exists an integer
$\|{G^{(\,j)}(0)}/{j!}\|_p\rightarrow 0$
. Hence, there exists an integer
![]() $\ell $
such that
$\ell $
such that
![]() $\nu _p(G^{(\,j)}(0)/j!)\geq -\ell $
for all j. Thus, we obtain
$\nu _p(G^{(\,j)}(0)/j!)\geq -\ell $
for all j. Thus, we obtain
![]() $G(mp^h)=G'(0)mp^h+d$
where
$G(mp^h)=G'(0)mp^h+d$
where
![]() $\nu _p(d)\geq 2h-\ell $
for all
$\nu _p(d)\geq 2h-\ell $
for all
![]() $m,h\geq 0$
. Also,
$m,h\geq 0$
. Also,
![]() $G(0)=0$
for
$G(0)=0$
for
![]() $h>h_0:=\ell +\nu _p(G'(0))$
and hence
$h>h_0:=\ell +\nu _p(G'(0))$
and hence
 $$ \begin{align*} \nu_p\bigg( \frac{G(mp^h)}{G(p^h)}-m\bigg)\geq h-h_0. \end{align*} $$
$$ \begin{align*} \nu_p\bigg( \frac{G(mp^h)}{G(p^h)}-m\bigg)\geq h-h_0. \end{align*} $$
This yields
 $$ \begin{align*} \lim_{h\rightarrow\infty}\bigg\lVert\frac{G(mp^h)}{G(p^h)}-m\bigg\rVert_p=0, \end{align*} $$
$$ \begin{align*} \lim_{h\rightarrow\infty}\bigg\lVert\frac{G(mp^h)}{G(p^h)}-m\bigg\rVert_p=0, \end{align*} $$
and hence
![]() $R(G(n)_{n\geq 0})$
is p-adically dense in
$R(G(n)_{n\geq 0})$
is p-adically dense in
![]() $\mathbb {N}$
. Since
$\mathbb {N}$
. Since
![]() $x_{nt}=G(n),n\geq 0$
, we find that
$x_{nt}=G(n),n\geq 0$
, we find that
![]() $R((x_n)_{n\geq 0})$
is also p-adically dense in
$R((x_n)_{n\geq 0})$
is also p-adically dense in
![]() $\mathbb {N}$
. Therefore, by Lemma 2.2,
$\mathbb {N}$
. Therefore, by Lemma 2.2,
![]() $R((x_n)_{n\geq 0})$
is dense in
$R((x_n)_{n\geq 0})$
is dense in
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
Proof of Corollary 1.4.
Since
![]() $p(1)p(-1){\kern-1pt}={\kern-1pt}(-a{\kern-1pt}-{\kern-1pt}b)(b{\kern-1pt}-{\kern-1pt}a{\kern-1pt}-{\kern-1pt}2){\kern-1pt}>{\kern-1pt}0$
and
$p(1)p(-1){\kern-1pt}={\kern-1pt}(-a{\kern-1pt}-{\kern-1pt}b)(b{\kern-1pt}-{\kern-1pt}a{\kern-1pt}-{\kern-1pt}2){\kern-1pt}>{\kern-1pt}0$
and
![]() $p(0){\kern-1pt}=-1$
, by continuity of the polynomial function in
$p(0){\kern-1pt}=-1$
, by continuity of the polynomial function in
![]() $\mathbb {R}$
,
$\mathbb {R}$
,
![]() $p(x)$
has one real root with absolute value greater than 1 and two other roots with absolute values less than
$p(x)$
has one real root with absolute value greater than 1 and two other roots with absolute values less than
![]() $1$
. Hence, the characteristic polynomial has a root
$1$
. Hence, the characteristic polynomial has a root
![]() $\pm \alpha$
, where
$\pm \alpha$
, where
![]() $\alpha$
is a Pisot number, and the corollary follows from Theorem 1.3.
$\alpha$
is a Pisot number, and the corollary follows from Theorem 1.3.
We need the following result to prove Theorem 1.7.
Corollary 3.2 [Reference Cîrnu9, Corollary 2.2].
The linear recurrence relation
![]() $x_{n+1}=x_n+2x_{n-1}+\cdots +nx_1+(n+1)x_0,n\geq 0$
, with the initial data
$x_{n+1}=x_n+2x_{n-1}+\cdots +nx_1+(n+1)x_0,n\geq 0$
, with the initial data
![]() $x_0=1$
has the solution
$x_0=1$
has the solution
 $$ \begin{align*}x_n=\frac{1}{\sqrt{5}}\bigg({\bigg(\frac{3+\sqrt{5}}{2}\bigg)}^n-{\bigg(\frac{3-\sqrt{5}}{2}\bigg)}^n\bigg),\quad n\geq 1.\end{align*} $$
$$ \begin{align*}x_n=\frac{1}{\sqrt{5}}\bigg({\bigg(\frac{3+\sqrt{5}}{2}\bigg)}^n-{\bigg(\frac{3-\sqrt{5}}{2}\bigg)}^n\bigg),\quad n\geq 1.\end{align*} $$
Proof of Theorem 1.7.
By Corollary 3.2, for
![]() $n\geq 1$
,
$n\geq 1$
,
 $$ \begin{align*} x_n=\frac{1}{\sqrt{5}}\bigg({\bigg(\frac{3+\sqrt{5}}{2}\bigg)}^n-{\bigg(\frac{3-\sqrt{5}}{2}\bigg)}^n\bigg) =\frac{\alpha^{2n}-\beta^{2n}}{\sqrt{5}} =F_{2n}, \end{align*} $$
$$ \begin{align*} x_n=\frac{1}{\sqrt{5}}\bigg({\bigg(\frac{3+\sqrt{5}}{2}\bigg)}^n-{\bigg(\frac{3-\sqrt{5}}{2}\bigg)}^n\bigg) =\frac{\alpha^{2n}-\beta^{2n}}{\sqrt{5}} =F_{2n}, \end{align*} $$
where
![]() $\alpha ={(1+\sqrt {5})}/{2}, \beta ={(1-\sqrt {5})}/{2}$
and
$\alpha ={(1+\sqrt {5})}/{2}, \beta ={(1-\sqrt {5})}/{2}$
and
![]() $F_n$
denotes the nth Fibonacci number which is obtained by the Binet formula. From [Reference Garcia and Luca14], the ratio set of the Fibonacci numbers is dense in
$F_n$
denotes the nth Fibonacci number which is obtained by the Binet formula. From [Reference Garcia and Luca14], the ratio set of the Fibonacci numbers is dense in
![]() $\mathbb {Q}_p$
for all primes p. Therefore, by Lemma 2.1,
$\mathbb {Q}_p$
for all primes p. Therefore, by Lemma 2.1,
![]() $\nu _p(F_n)$
is not bounded. Hence, for any
$\nu _p(F_n)$
is not bounded. Hence, for any
![]() $j\in \mathbb {N}$
, there exists
$j\in \mathbb {N}$
, there exists
![]() $F_m$
such that
$F_m$
such that
![]() $\nu _p(F_m)\geq j$
, that is,
$\nu _p(F_m)\geq j$
, that is,
![]() ${(\alpha ^{m}-\beta ^{m})}/{\sqrt {5}}\equiv 0 \pmod {p^{\,j}}$
which gives
${(\alpha ^{m}-\beta ^{m})}/{\sqrt {5}}\equiv 0 \pmod {p^{\,j}}$
which gives
![]() $\alpha ^m\equiv \beta ^m\pmod {p^{\,j}}$
. This yields
$\alpha ^m\equiv \beta ^m\pmod {p^{\,j}}$
. This yields
Since
![]() $\alpha \beta =-1$
, by using Euler’s theorem, we find that
$\alpha \beta =-1$
, by using Euler’s theorem, we find that
This gives
![]() $\alpha ^{2k}\equiv \beta ^{2k}\equiv 1\pmod {p^{\,j}}$
, where
$\alpha ^{2k}\equiv \beta ^{2k}\equiv 1\pmod {p^{\,j}}$
, where
![]() $k=mp^{\,j-1}(p-1)$
. Hence,
$k=mp^{\,j-1}(p-1)$
. Hence,
 $$ \begin{align*} \frac{x_{kn}}{x_{k}}=\frac{F_{2kn}}{F_{2k}}=\frac{(\alpha^{2k})^n-(\beta^{2k})^n}{\alpha^{2k}-\beta^{2k}}=(\alpha^{2k})^{(n-1)}+(\alpha^{2k})^{n-2}\beta^{2k}+\cdots+(\beta^{2k})^{n-1}, \end{align*} $$
$$ \begin{align*} \frac{x_{kn}}{x_{k}}=\frac{F_{2kn}}{F_{2k}}=\frac{(\alpha^{2k})^n-(\beta^{2k})^n}{\alpha^{2k}-\beta^{2k}}=(\alpha^{2k})^{(n-1)}+(\alpha^{2k})^{n-2}\beta^{2k}+\cdots+(\beta^{2k})^{n-1}, \end{align*} $$
which is congruent to n modulo
![]() $p^{\,j}$
. Since, for
$p^{\,j}$
. Since, for
![]() $n\in \mathbb {N}$
, there exists
$n\in \mathbb {N}$
, there exists
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $\|{x_{kn}}/{x_k}-n\|_p\leq p^{-j}$
,
$\|{x_{kn}}/{x_k}-n\|_p\leq p^{-j}$
,
![]() $R((x_n)_{n\geq 0})$
is p-adically dense in
$R((x_n)_{n\geq 0})$
is p-adically dense in
![]() $\mathbb {N}$
. Therefore, by Lemma 2.2,
$\mathbb {N}$
. Therefore, by Lemma 2.2,
![]() $R((x_n)_{n\geq 0})$
is dense in
$R((x_n)_{n\geq 0})$
is dense in
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
We need the following results to prove Theorem 1.8.
Theorem 3.3 [Reference Cîrnu9, Theorem 3.1].
The numbers
![]() $x_n$
are solutions of the linear recurrence relation with constant coefficients in geometric progression
$x_n$
are solutions of the linear recurrence relation with constant coefficients in geometric progression
![]() $x_{n+1}=ax_n+aqx_{n-1}+\cdots +aq^{n-1}x_1+aq^nx_0,n\geq 0$
, with initial data
$x_{n+1}=ax_n+aqx_{n-1}+\cdots +aq^{n-1}x_1+aq^nx_0,n\geq 0$
, with initial data
![]() $x_0$
, if and only if they form the geometric progression given by the formula
$x_0$
, if and only if they form the geometric progression given by the formula
![]() $x_n=ax_0(a+q)^{n-1},n\geq 1$
.
$x_n=ax_0(a+q)^{n-1},n\geq 1$
.
Lemma 3.4 [Reference Garcia, Hong, Luca, Pinsker, Sanna, Schechter and Starr13, Lemma 2.2].
If A is a geometric progression in
![]() $\mathbb {Z}$
, then
$\mathbb {Z}$
, then
![]() $R(A)$
is not dense in any
$R(A)$
is not dense in any
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
Proof of Theorem 1.8.
By Theorem 3.3,
![]() $(x_n)_{n\geq 1}$
forms a geometric progression whose nth term is
$(x_n)_{n\geq 1}$
forms a geometric progression whose nth term is
![]() $ax_0(a+r)^{n-1}$
for
$ax_0(a+r)^{n-1}$
for
![]() $n\geq 1$
. Hence, by Lemma 3.4,
$n\geq 1$
. Hence, by Lemma 3.4,
![]() $R((x_n)_{n\geq 0})$
is not dense in
$R((x_n)_{n\geq 0})$
is not dense in
![]() $\mathbb {Q}_p$
for any prime p.
$\mathbb {Q}_p$
for any prime p.
To prove Theorem 1.9 we need some results on the uniform distribution of sequences of integers. Recall that a sequence
![]() $(x_n)_{n\geq 0}$
is said to be uniformly distributed modulo m if each residue occurs equally often, that is,
$(x_n)_{n\geq 0}$
is said to be uniformly distributed modulo m if each residue occurs equally often, that is,
Proposition 3.5 [Reference Bumby8, Proposition 1].
Suppose
![]() $(G_n)_{n\ge 0}$
is the sequence of integers determined by the recurrence relation
$(G_n)_{n\ge 0}$
is the sequence of integers determined by the recurrence relation
![]() $G_{n+1}=AG_n-BG_{n-1}$
with initial values
$G_{n+1}=AG_n-BG_{n-1}$
with initial values
![]() $G_0,G_1$
where
$G_0,G_1$
where
![]() $A,B,G_0,G_1\in \mathbb {Z}$
. If
$A,B,G_0,G_1\in \mathbb {Z}$
. If
![]() $A=2a,B=a^2$
, then
$A=2a,B=a^2$
, then
![]() $(G_n)_{n\ge 0}$
is uniformly distributed modulo a prime p if and only if
$(G_n)_{n\ge 0}$
is uniformly distributed modulo a prime p if and only if
![]() $p\nmid a(G_1-aG_0)$
.
$p\nmid a(G_1-aG_0)$
.
Theorem 3.6 [Reference Bumby8, Theorem].
Suppose
![]() $(G_n)_{n\ge 0}$
is the sequence of integers determined by the recurrence relation
$(G_n)_{n\ge 0}$
is the sequence of integers determined by the recurrence relation
![]() $G_{n+1}=AG_n-BG_{n-1}$
with initial values
$G_{n+1}=AG_n-BG_{n-1}$
with initial values
![]() $G_0,G_1$
where
$G_0,G_1$
where
![]() $A,B,G_0,G_1\in \mathbb {Z}$
. If
$A,B,G_0,G_1\in \mathbb {Z}$
. If
![]() $(G_n)_{n\ge 0}$
is uniformly distributed modulo p, then
$(G_n)_{n\ge 0}$
is uniformly distributed modulo p, then
![]() $(G_n)_{n\ge 0}$
is uniformly distributed modulo
$(G_n)_{n\ge 0}$
is uniformly distributed modulo
![]() $p^h$
with
$p^h$
with
![]() $h>1$
if and only if
$h>1$
if and only if
-
(1)
 $p>3$
; or
$p>3$
; or -
(2)
 $p=3$
and
$p=3$
and
 $A^2\not \equiv B\pmod {9}$
; or
$A^2\not \equiv B\pmod {9}$
; or -
(3)
 $p=2, A\equiv 2\pmod {4},B\equiv 1\pmod {4}$
.
$p=2, A\equiv 2\pmod {4},B\equiv 1\pmod {4}$
.
Proof of Theorem 1.9.
Let p be a prime. The given recurrence sequence
![]() $(x_n)_{n\geq 0}$
satisfies the hypotheses of Proposition 3.5, and hence
$(x_n)_{n\geq 0}$
satisfies the hypotheses of Proposition 3.5, and hence
![]() $(x_n)_{n\geq 0}$
is uniformly distributed modulo p. If
$(x_n)_{n\geq 0}$
is uniformly distributed modulo p. If
![]() $p>3$
, then by Theorem 3.6(1),
$p>3$
, then by Theorem 3.6(1),
![]() $(x_n)_{n\geq 0}$
is uniformly distributed modulo
$(x_n)_{n\geq 0}$
is uniformly distributed modulo
![]() $p^k$
with
$p^k$
with
![]() $k>1$
, that is,
$k>1$
, that is,
 $$ \begin{align*}\lim_{N\rightarrow\infty}\frac{\# \{n\leq N\mid x _n\equiv t \pmod{p^k}\}}{N}=\frac{1}{p^k}>0.\end{align*} $$
$$ \begin{align*}\lim_{N\rightarrow\infty}\frac{\# \{n\leq N\mid x _n\equiv t \pmod{p^k}\}}{N}=\frac{1}{p^k}>0.\end{align*} $$
Therefore, for all
![]() $t\in \mathbb {N}$
and for all
$t\in \mathbb {N}$
and for all
![]() $k>1$
, there exists
$k>1$
, there exists
![]() $x_n$
such that
$x_n$
such that
![]() $\| x_n-t\|_p\leq p^{-k}$
. Hence,
$\| x_n-t\|_p\leq p^{-k}$
. Hence,
![]() $R((x_n)_{n\geq 0})$
is p-adically dense in
$R((x_n)_{n\geq 0})$
is p-adically dense in
![]() $\mathbb {N}$
. Therefore, by Lemma 2.2,
$\mathbb {N}$
. Therefore, by Lemma 2.2,
![]() $R((x_n)_{n\geq 0})$
is dense in
$R((x_n)_{n\geq 0})$
is dense in
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
We next consider the remaining primes
![]() $p=2,3$
. Since
$p=2,3$
. Since
![]() $p\nmid a(x_1-ax_0)$
, we have
$p\nmid a(x_1-ax_0)$
, we have
![]() $p\nmid a$
. It is easy to check that
$p\nmid a$
. It is easy to check that
![]() $p=3$
satisfies the condition given in Theorem 3.6(2) and
$p=3$
satisfies the condition given in Theorem 3.6(2) and
![]() $p=2$
satisfies the condition given in Theorem 3.6(3). The rest of the proof follows similarly as shown in the case
$p=2$
satisfies the condition given in Theorem 3.6(3). The rest of the proof follows similarly as shown in the case
![]() $p>3$
. This completes the proof of the theorem.
$p>3$
. This completes the proof of the theorem.
We need the following lemma to prove Theorem 1.10.
Lemma 3.7 [Reference Sanna26, Lemma 3.3].
Let
![]() $(r_n)_{n\geq 0}$
be a linearly recurring sequence of order
$(r_n)_{n\geq 0}$
be a linearly recurring sequence of order
![]() $k\geq 2$
given by
$k\geq 2$
given by
![]() $r_n=a_1r_{n-1}+\cdots +a_k r_{n-k}$
for each integer
$r_n=a_1r_{n-1}+\cdots +a_k r_{n-k}$
for each integer
![]() $n\geq k$
, where
$n\geq k$
, where
![]() $r_0,\ldots ,r_{k-1}$
and
$r_0,\ldots ,r_{k-1}$
and
![]() $a_1,\ldots ,a_k$
are all integers. Suppose that there exists a prime number p such that
$a_1,\ldots ,a_k$
are all integers. Suppose that there exists a prime number p such that
![]() $p\nmid a_k$
and
$p\nmid a_k$
and
![]() $\min \{\nu _p(a_j):1\leq j<k\}>\max \{\nu _p(r_m)-\nu _p(r_n):0\leq m,n<k\}$
. Then
$\min \{\nu _p(a_j):1\leq j<k\}>\max \{\nu _p(r_m)-\nu _p(r_n):0\leq m,n<k\}$
. Then
![]() $\nu _p(r_n)=\nu _p(r_{n\pmod {k}})$
for each nonnegative integer n.
$\nu _p(r_n)=\nu _p(r_{n\pmod {k}})$
for each nonnegative integer n.
Proof of Theorem 1.10.
By Lemma 3.7,
for all
![]() $n,m\in \mathbb {N}\cup \{0\}$
, where
$n,m\in \mathbb {N}\cup \{0\}$
, where
![]() $M=\max \{\nu _p(x_i):i=0,1,\ldots ,k-1\}$
. Therefore, by Lemma 2.1,
$M=\max \{\nu _p(x_i):i=0,1,\ldots ,k-1\}$
. Therefore, by Lemma 2.1,
![]() $R((x_n)_{n\geq 0})$
is not dense in
$R((x_n)_{n\geq 0})$
is not dense in
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
Acknowledgements
We are very grateful to the referee for a careful reading of the paper and for comments which helped us to make improvements. We thank Piotr Miska for many helpful discussions.