No CrossRef data available.
Article contents
BINARY AND TERNARY CONGRUENCES INVOLVING INTERVALS AND SETS MODULO A PRIME
Published online by Cambridge University Press: 18 March 2025
Abstract
Let s be a fixed positive integer constant and let 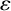 $\varepsilon $ be a fixed small positive number. Then, provided that a prime p is large enough, we prove that, for any set
$\varepsilon $ be a fixed small positive number. Then, provided that a prime p is large enough, we prove that, for any set 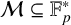 ${\mathcal M}\subseteq \mathbb {F}_p^*$ of size
${\mathcal M}\subseteq \mathbb {F}_p^*$ of size 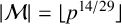 $|{\mathcal M}|= \lfloor { p^{14/29}}\rfloor $ and integer
$|{\mathcal M}|= \lfloor { p^{14/29}}\rfloor $ and integer 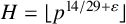 $H=\lfloor {p^{14/29+\varepsilon }}\rfloor $, any integer
$H=\lfloor {p^{14/29+\varepsilon }}\rfloor $, any integer 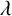 $\lambda $ can be represented in the form
$\lambda $ can be represented in the form 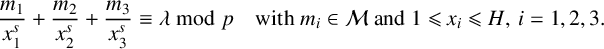 $$ \begin{align*} \frac{m_1}{x_1^s}+\frac{m_2}{x_2^s}+\frac{m_3}{x_3^s}\equiv \lambda \bmod p \quad\text{with } m_i\in {\mathcal M} \text{ and } 1\leqslant x_i\leqslant H, \, i=1,2,3. \end{align*} $$
$$ \begin{align*} \frac{m_1}{x_1^s}+\frac{m_2}{x_2^s}+\frac{m_3}{x_3^s}\equiv \lambda \bmod p \quad\text{with } m_i\in {\mathcal M} \text{ and } 1\leqslant x_i\leqslant H, \, i=1,2,3. \end{align*} $$
When 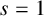 $s=1$, we show that, for almost all primes p, if
$s=1$, we show that, for almost all primes p, if 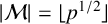 $|{\mathcal M}|= \lfloor p^{1/2}\rfloor $ and
$|{\mathcal M}|= \lfloor p^{1/2}\rfloor $ and 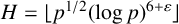 $H=\lfloor p^{1/2}(\log p)^{6+\varepsilon }\rfloor $, then any integer
$H=\lfloor p^{1/2}(\log p)^{6+\varepsilon }\rfloor $, then any integer 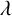 $\lambda $ can be represented in the form
$\lambda $ can be represented in the form 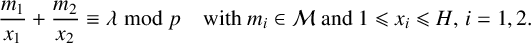 $$ \begin{align*} \frac{m_1}{x_1}+\frac{m_2}{x_2}\equiv \lambda \bmod p \quad\text{with } m_i\in {\mathcal M} \text{ and } 1\leqslant x_i\leqslant H, \, i=1,2. \end{align*} $$
$$ \begin{align*} \frac{m_1}{x_1}+\frac{m_2}{x_2}\equiv \lambda \bmod p \quad\text{with } m_i\in {\mathcal M} \text{ and } 1\leqslant x_i\leqslant H, \, i=1,2. \end{align*} $$
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc
Footnotes
The third author was partially supported by ARC Grants DP230100530 and DP230100534.


