No CrossRef data available.
Article contents
Beurling's ordinary value
Published online by Cambridge University Press: 17 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let n(w, f) be the number of w-points of f meromorphic in D = {|z| < 1}. Beurling defined the quantity 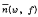 and called w an ordinary value of f if
and called w an ordinary value of f if 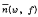 < ∞. We shall consider the intermediate quantity ṉ(w, f) in the sense that n(w, f) ≤ ṉ(w, f)
< ∞. We shall consider the intermediate quantity ṉ(w, f) in the sense that n(w, f) ≤ ṉ(w, f) 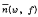 , and construct two bounded holo-morphic functions f1 and f2 of finite Dirichlet integrals in D for which
, and construct two bounded holo-morphic functions f1 and f2 of finite Dirichlet integrals in D for which
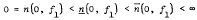
and
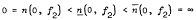 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1983
References
[2]Saks, Stanislaw, Theory of the integral, second revised edition (translated by Young, L.C.. Monografie Matematyczne, 7. Hafner, New York, 1937).Google Scholar

