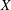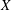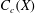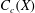Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
FERRANDO, JUAN CARLOS
2015.
BARRELLEDNESS OF SOME SPACES OF VECTOR MEASURES AND BOUNDED LINEAR OPERATORS.
Bulletin of the Korean Mathematical Society,
Vol. 52,
Issue. 5,
p.
1579.
Saxon, Stephen A.
2016.
(LF)-spaces with more-than-separable quotients.
Journal of Mathematical Analysis and Applications,
Vol. 434,
Issue. 1,
p.
12.
Ka̧kol, Jerzy
Leiderman, Arkady G.
and
Morris, Sidney A.
2017.
Nonseparable closed vector subspaces of separable topological vector spaces.
Monatshefte für Mathematik,
Vol. 182,
Issue. 1,
p.
39.
Ka̧kol, Jerzy
and
Saxon, Stephen
2017.
Separable quotients in 𝐶_{𝑐}(𝑋), 𝐶_{𝑝}(𝑋), and their duals.
Proceedings of the American Mathematical Society,
Vol. 145,
Issue. 9,
p.
3829.
Ka̧kol, Jerzy
and
Saxon, Stephen A.
2018.
Separable quotients for less-than-barrelled function spaces.
Journal of Mathematical Analysis and Applications,
Vol. 459,
Issue. 2,
p.
1102.
Ka̧kol, J.
and
Śliwa, W.
2018.
Efimov spaces and the separable quotient problem for spaces C(K).
Journal of Mathematical Analysis and Applications,
Vol. 457,
Issue. 1,
p.
104.
Banakh, Taras
Ka̧kol, Jerzy
and
Śliwa, Wiesław
2018.
Metrizable quotients of C-spaces.
Topology and its Applications,
Vol. 249,
Issue. ,
p.
95.
Ferrando, Juan C.
Kąkol, Jerzy
López-Pellicer, Manuel
and
Śliwa, Wiesław
2018.
On the separable quotient problem for Banach spaces.
Functiones et Approximatio Commentarii Mathematici,
Vol. 59,
Issue. 2,
Leiderman, Arkady
and
Morris, Sidney
2018.
Separability of Topological Groups: A Survey with Open Problems.
Axioms,
Vol. 8,
Issue. 1,
p.
3.
Leiderman, Arkady G.
Morris, Sidney A.
and
Tkachenko, Mikhail G.
2019.
The separable quotient problem for topological groups.
Israel Journal of Mathematics,
Vol. 234,
Issue. 1,
p.
331.
Gabriyelyan, Saak S.
and
Morris, Sidney A.
2019.
A topological group observation on the Banach–Mazur separable quotient problem.
Topology and its Applications,
Vol. 259,
Issue. ,
p.
283.
Kąkol, Jerzy
and
Saxon, Stephen A.
2019.
The quotient/codimension problems.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 113,
Issue. 2,
p.
1429.
Kumar, Akshay
and
Jindal, Varun
2024.
Extended locally convex spaces: Barreledness, equicontinuity and Banach-Steinhaus theorem.
Topology and its Applications,
Vol. 348,
Issue. ,
p.
108890.