No CrossRef data available.
Article contents
BACKWARD 3-STEP EXTENSIONS OF RECURSIVELY GENERATED WEIGHTED SHIFTS: A RANGE OF QUADRATIC HYPONORMALITY
Part of:
Special classes of linear operators
Published online by Cambridge University Press: 20 November 2013
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 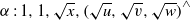 $\alpha : 1, 1, \sqrt{x} , \mathop{( \sqrt{u} , \sqrt{v} , \sqrt{w} )}\nolimits ^{\wedge } $ be a backward 3-step extension of a recursively generated weighted sequence of positive real numbers with
$\alpha : 1, 1, \sqrt{x} , \mathop{( \sqrt{u} , \sqrt{v} , \sqrt{w} )}\nolimits ^{\wedge } $ be a backward 3-step extension of a recursively generated weighted sequence of positive real numbers with 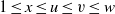 $1\leq x\leq u\leq v\leq w$ and let
$1\leq x\leq u\leq v\leq w$ and let 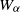 ${W}_{\alpha } $ be the associated weighted shift with weight sequence
${W}_{\alpha } $ be the associated weighted shift with weight sequence  $\alpha $. The set of positive real numbers
$\alpha $. The set of positive real numbers  $x$ such that
$x$ such that 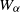 ${W}_{\alpha } $ is quadratically hyponormal for some
${W}_{\alpha } $ is quadratically hyponormal for some 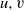 $u, v$ and
$u, v$ and 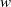 $w$ is described, solving an open problem due to Curto and Jung [‘Quadratically hyponormal weighted shifts with two equal weights’, Integr. Equ. Oper. Theory 37 (2000), 208–231].
$w$ is described, solving an open problem due to Curto and Jung [‘Quadratically hyponormal weighted shifts with two equal weights’, Integr. Equ. Oper. Theory 37 (2000), 208–231].
Information
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
Bae, J. Y., Exner, G. and Jung, I. B., ‘Criteria for positively quadratically hyponormal weighted shifts’, Proc. Amer. Math. Soc. 130 (2002), 3287–3294.CrossRefGoogle Scholar
Curto, R., ‘Joint hyponormality: a bridge between hyponormality and subnormality’, Proc. Sympos. Pure Math. 51 (1990), 69–91.CrossRefGoogle Scholar
Curto, R., ‘Quadratically hyponormal weighted shifts’, Integr. Equ. Oper. Theory 13 (1990), 49–66.CrossRefGoogle Scholar
Curto, R., ‘Polynomially hyponormal operators on Hilbert space’, Proc. ELAM VII Revista Union Mat. Arg. 37 (1991), 29–56.Google Scholar
Curto, R. and Fialkow, L., ‘Recursively generated weighted shifts and the subnormal completion problem, II’, Integr. Equ. Oper. Theory 18 (1994), 369–426.Google Scholar
Curto, R. and Jung, I. B., ‘Quadratically hyponormal weighted shifts with two equal weights’, Integr. Equ. Oper. Theory 37 (2000), 208–231.Google Scholar
Curto, R. and Lee, W. Y., ‘Solution of the quadratically hyponormal completion problem’, Proc. Amer. Math. Soc. 131 (2003), 2479–2489.Google Scholar
Exner, G., Jung, I. B., Lee, M. R. and Park, S. H., ‘Quadratically hyponormal weighted shifts with recursive tail’, J. Math. Anal. Appl. 408 (2013), 298–305.Google Scholar
Exner, G., Jung, I. B. and Park, D. W., ‘Some quadratically hyponormal weighted shifts’, Integr. Equ. Oper. Theory 60 (2008), 13–36.CrossRefGoogle Scholar
Jung, I. B. and Park, S. S., ‘Quadratically hyponormal weighted shifts and their examples’, Integr. Equ. Oper. Theory 36 (2002), 480–498.Google Scholar
Poon, Y. T. and Yoon, J., ‘Quadratically hyponormal recursively generated weighted shifts need not be positively quadratically hyponormal’, Integr. Equ. Oper. Theory 58 (2007), 551–562.Google Scholar
Stampfli, J., ‘Which weighted shifts are subnormal’, Pacific J. Math. 17 (1966), 367–379.CrossRefGoogle Scholar

