Article contents
(ANTI)COMMUTATIVE ALGEBRAS WITH A MULTIPLICATIVE BASIS
Published online by Cambridge University Press: 15 December 2014
Abstract
A basis 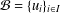 ${\mathcal{B}}=\{u_{i}\}_{i\in I}$ of a commutative or anticommutative algebra
${\mathcal{B}}=\{u_{i}\}_{i\in I}$ of a commutative or anticommutative algebra  $\mathfrak{C},$ over an arbitrary base field
$\mathfrak{C},$ over an arbitrary base field 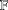 $\mathbb{F}$, is called multiplicative if for any
$\mathbb{F}$, is called multiplicative if for any 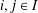 $i,j\in I$ we have that
$i,j\in I$ we have that 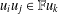 $u_{i}u_{j}\in \mathbb{F}u_{k}$ for some
$u_{i}u_{j}\in \mathbb{F}u_{k}$ for some 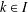 $k\in I$. We show that if a commutative or anticommutative algebra
$k\in I$. We show that if a commutative or anticommutative algebra 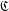 $\mathfrak{C}$ admits a multiplicative basis then it decomposes as the direct sum
$\mathfrak{C}$ admits a multiplicative basis then it decomposes as the direct sum 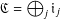 $\mathfrak{C}=\bigoplus _{j}\mathfrak{i}_{j}$ of well-described ideals each one of which admits a multiplicative basis. Also the minimality of
$\mathfrak{C}=\bigoplus _{j}\mathfrak{i}_{j}$ of well-described ideals each one of which admits a multiplicative basis. Also the minimality of 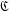 $\mathfrak{C}$ is characterised in terms of the multiplicative basis and it is shown that, under a mild condition, the above direct sum is indexed by the family of its minimal ideals admitting a multiplicative basis.
$\mathfrak{C}$ is characterised in terms of the multiplicative basis and it is shown that, under a mild condition, the above direct sum is indexed by the family of its minimal ideals admitting a multiplicative basis.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © 2014 Australian Mathematical Publishing Association Inc.
References
- 2
- Cited by

