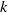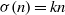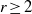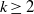Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vavilov, N. A.
2023.
Computers As a Novel Mathematical Reality: III. Mersenne Numbers and Sums of Divisors.
Doklady Mathematics,
Vol. 107,
Issue. 3,
p.
173.