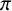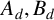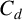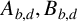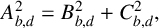1 Introduction
One of the most famous identities of Jacobi states that
$$ \begin{align} \bigg(\sum_{m,n=-\infty}^\infty q^{m^2+n^2}\bigg)^2=\bigg(\sum_{m,n=-\infty}^\infty (-1)^{m+n} q^{m^2+n^2}\bigg)^2+\bigg(\sum_{m,n=-\infty}^\infty q^{(m+1/2)^2+(n+1/2)^2}\bigg)^2. \end{align} $$
One can view (1.1) as a solution to
$$ \begin{align} A^2=B^2+C^2, \end{align} $$
where
$A,B$
and C are theta series of weight one. This identity is instrumental in the parametrisation of Gauss’ arithmetic–geometric mean by modular forms [Reference Borwein and Borwein2, Reference Solé and Loyer8].
In [Reference Chan, Chua and Solé5], Chan et al., motivated by the study of codes and lattices, found that, for any positive integer d,
$$ \begin{align} \bigg(\sum_{m,n=-\infty}^\infty q^{2(m^2+mn+dn^2)}\bigg)^2 & =\bigg(\sum_{m,n=-\infty}^\infty (-1)^{m+n} q^{m^2+mn+dn^2}\bigg)^2 \notag \\ &\quad +\bigg(\sum_{m,n=-\infty}^\infty q^{2((m+1/2)^2+(m+1/2)n+dn^2)}\bigg)^2. \end{align} $$
Identity (1.3) provides an infinite number of solutions in theta functions of weight one to (1.2). For more information on this generalised Jacobi identity, see [Reference Chan, Chua and Solé6, Reference Chua and Solé7].
Recently, while studying theta series associated with binary quadratic forms of discriminant
$-15$
, we discovered the identity
$$ \begin{align} \bigg(\sum_{m,n=-\infty}^\infty q^{2m^2+mn+2n^2}\bigg)^2 & = \bigg(\sum_{m,n=-\infty}^\infty (-1)^{m+n} q^{2m^2+mn+2n^2}\bigg)^2 \notag \\ &\quad +\bigg(2\sum_{m,n=-\infty}^\infty q^{2(2(m+1/2)^2+(m+1/2)n+2n^2)}\bigg)^2. \end{align} $$
We establish the following analogue of (1.3) for which (1.4) is a special case.
Theorem 1.1. Let d be any positive integer and let
$1\leq b\leq d-1$
. Then
$$ \begin{align} \bigg(\sum_{m,n=-\infty}^\infty q^{dm^2+bmn+dn^2} \bigg)^2 &=\bigg(\sum_{m,n=-\infty}^\infty (-1)^{m+n} q^{dm^2+bmn+dn^2}\bigg)^2 \notag \\ &\quad + \bigg(2\sum_{m,n=-\infty}^\infty q^{2(d(m+1/2)^2+b(m+1/2)n+dn^2)}\bigg)^2. \end{align} $$
When
$d=2$
and
$b=1$
, we recover (1.4) from (1.5). The proof of (1.5) is given in Section 2.
Our discovery of (1.5) provides a motivation for deriving the following two-variable version of (1.3): that is,
$$ \begin{align} \bigg(\sum_{m,n=-\infty}^\infty q^{2(bm^2+bmn+dn^2)}\bigg)^2 & =\bigg(\sum_{m,n=-\infty}^\infty (-1)^{m+n} q^{bm^2+bmn+dn^2}\bigg)^2 \notag \\ &\quad +\bigg(\sum_{m,n=-\infty}^\infty q^{2(b(m+1/2)^2+b(m+1/2)n+dn^2)}\bigg)^2. \end{align} $$
Observe that, when
$b=1$
, (1.6) implies (1.3). We give a proof of (1.6) in Section 3.
2 Proof of (1.5)
The Jacobi one-variable theta functions are defined by
$$ \begin{align*} \vartheta_2(q) &= \sum_{j=-\infty}^\infty q^{(j+1/2)^2},\\ \vartheta_3(q) &= \sum_{j=-\infty}^\infty q^{j^2}\end{align*} $$
and
$$ \begin{align*} \vartheta_4(q) &= \sum_{j=-\infty}^\infty (-1)^jq^{j^2}. \end{align*} $$
We first express the theta functions in (1.5) in terms of
$\vartheta _j(q), j=2,3,4$
.
Lemma 2.1. For
$|q|<1$
,
$$ \begin{align} &\mathcal A_{b,d}=\sum_{m,n=-\infty}^\infty q^{dm^2+bmn+dn^2} = \vartheta_3(q^{2d+b})\vartheta_3(q^{2d-b}) +\vartheta_2(q^{2d+b})\vartheta_2(q^{2d-b}),\quad\qquad \end{align} $$
$$ \begin{align} &\mathcal B_{b,d}=\sum_{m,n=-\infty}^\infty (-1)^{m+n}q^{dm^2+bmn+dn^2} = \vartheta_3(q^{2d+b})\vartheta_3(q^{2d-b}) -\vartheta_2(q^{2d+b})\vartheta_2(q^{2d-b}) \end{align} $$
and
$$ \begin{align} &\mathcal C_{b,d}=2\sum_{m,n=-\infty}^\infty q^{2(d(m+1/2)^2+b(m+1/2)n+dn^2)} = \vartheta_2(q^{d+b/2})\vartheta_2(q^{d-b/2}). \end{align} $$
Proof. We observe that
$$ \begin{align*}dm^2+bmn+dn^2 =\begin{pmatrix} m & n \end{pmatrix}\begin{pmatrix} d & b/2 \\ b/2 & d\end{pmatrix} \begin{pmatrix} m \\ n \end{pmatrix}.\end{align*} $$
Next, since
$$ \begin{align*}\begin{pmatrix} d & b/2 \\ b/2 & d\end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} d+b/2 & 0 \\ 0 & d-b/2 \end{pmatrix} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix},\end{align*} $$
we find that
$$ \begin{align*}dm^2+bmn+dn^2 = \dfrac{2d+b}{4}(m+n)^2 +\dfrac{2d-b}{4}(m-n)^2.\end{align*} $$
Therefore,
$$ \begin{align*} &\sum_{m,n=-\infty}^\infty q^{dm^2+bmn+dn^2} = \sum_{m,n=-\infty}^\infty q^{(2d+b)(m+n)^2/4+(2d-b)(m-n)^2/4}\\ &\quad =\sum_{\substack{m,n=-\infty\\ m+n \text{ even}}}^\infty q^{(2d+b)(m+n)^2/4+(2d-b)(m-n)^2/4}+ \sum_{\substack{m,n=-\infty\\ m+n \text{ odd}}}^\infty q^{(2d+b)(m+n)^2/4+(2d-b)(m-n)^2/4}\\ &\quad =\vartheta_3(q^{2d+b})\vartheta_3(q^{2d-b})+\vartheta_2(q^{2d+b})\vartheta_2(q^{2d-b}), \end{align*} $$
which completes the proof of (2.1). The proof of (2.2) is similar to the proof of (2.1).
To prove (2.3), we need the identity
$$ \begin{align} \sum_{m=-\infty}^\infty (-1)^mq^{(m+1/2)^2} = 0.\end{align} $$
Identity (2.4) is true because
$$ \begin{align*}\sum_{m=-\infty}^\infty (-1)^m q^{(m+1/2)^2} = \sum_{s=-\infty}^\infty (-1)^s q^{(s-1/2)^2} =\sum_{t=-\infty}^\infty (-1)^{t+1} q^{(t+1/2)^2}.\end{align*} $$
From (2.4), we deduce that, for any integer
$\ell $
,
$$ \begin{align} \sum_{m=-\infty}^\infty (-1)^mq^{(m+\ell+1/2)^2} = 0.\end{align} $$
A consequence of (2.5) is that
$$ \begin{align} \sum_{n=-\infty}^\infty q^{(2n+\ell+1/2)^2}=\sum_{n=-\infty}^\infty q^{(2n+1+\ell+1/2)^2}. \end{align} $$
We are now ready to prove (2.3). Write
$$ \begin{align*}\mathcal C_{b,d} = 2\sum_{m,n=-\infty}^\infty q^{(2d+b)(m+1/2+n)^2/2+(2d-b)(m+1/2-n)^2/2}.\end{align*} $$
Let
$k=m-n.$
Then
$$ \begin{align*}\mathcal C_{b,d} &= 2\sum_{k=-\infty}^\infty q^{(2d-b)(k+1/2)^2/2}\sum_{n=-\infty}^\infty q^{(2d+b)(2n+k+1/2)^2/2}\\ &=\sum_{k=-\infty}^\infty q^{(2d-b)(k+1/2)^2/2}\sum_{s=-\infty}^\infty q^{(2d+b)(s+1/2)^2/2}=\vartheta_2(q^{(2d-b)/2})\vartheta_2(q^{(2d+b)/2}), \end{align*} $$
which is (2.3). The last equality follows by writing
$$ \begin{align*} 2\sum_{n=-\infty}^\infty q^{(2d+b)(2n+k+1/2)^2/2}&= \sum_{n=-\infty}^\infty q^{(2d+b)(2n+k+1/2)^2/2}+\sum_{n=-\infty}^\infty q^{(2d+b)(2n+k+1+1/2)^2/2}\\ &=\sum_{s=-\infty}^\infty q^{(2d+b)(s+1/2)^2/2}, \end{align*} $$
where we have used (2.6) in the first equality.
Using (2.1) and (2.2), we deduce that
$$ \begin{align*}\mathcal A_{b,d}^2 -\mathcal B_{b,d}^2 = 4\vartheta_2(q^{2d+b})\vartheta_2(q^{2d-b})\vartheta_3(q^{2d+b})\vartheta_3(q^{2d-b}) .\end{align*} $$
Next, it is known from Jacobi’s triple product identity that
$$ \begin{align*} \vartheta_2(q) = 2q^{1/4}\prod_{j=1}^\infty (1-q^{2j})(1+q^{2j})^2 \end{align*} $$
and
$$ \begin{align*}\vartheta_3(q) = \prod_{j=1}^\infty (1-q^{2j})(1+q^{2j-1})^2.\end{align*} $$
Therefore,
$$ \begin{align} 2\vartheta_2(q^2)\vartheta_3(q^2) = \vartheta_2^2(q).\end{align} $$
Replacing
$q^2$
by q and using (2.3), we deduce that
$$ \begin{align*}\mathcal A_{b,d}^2 -\mathcal B_{b,d}^2 =\mathcal C_{b,d}^2\end{align*} $$
and the proof of (1.5) is complete.
It is possible to derive (2.7) without using Jacobi’s triple product identity. For more details, see [Reference Chan4, page 58].
When
$d=1$
and
$b=0$
, (1.5) becomes
$$ \begin{align*} \bigg(\sum_{m,n=-\infty}^\infty q^{m^2+n^2} \bigg)^2 =\bigg(\sum_{m,n=-\infty}^\infty (-1)^{m+n} q^{m^2+n^2}\bigg)^2 + \bigg(2\sum_{m,n=-\infty}^\infty q^{2((m+1/2)^2+n^2)}\bigg)^2, \end{align*} $$
which reduces to
$$ \begin{align} \vartheta_3^4(q)=\vartheta_4^4(q) + 4\vartheta_2^2(q^2)\vartheta_3^2(q^2).\end{align} $$
By (2.7), we arrive at (1.1). Next, (2.8) can then be written as
$$ \begin{align}\vartheta_3^4(q)+\vartheta_2^4(q)=\vartheta_3^4(q)-\vartheta_2^4(q) + 8 \vartheta_2^2(q^2)\vartheta_3^2(q^2). \end{align} $$
Identity (2.9) appeared in [Reference Berndt, Chan and Liaw1, page 140] and the functions
$$ \begin{align*}\vartheta_3^4(q)+\vartheta_2^4(q), \quad \vartheta_3^4(q)-\vartheta_2^4(q) =\vartheta_4^4(q) \quad\text{and} \quad 2\vartheta_2^2(q)\vartheta_3^2(q)\end{align*} $$
play important roles in Ramanujan’s theory of elliptic functions to the quartic base (see [Reference Borwein and Borwein3, Theorem 2.6(b)] and [Reference Berndt, Chan and Liaw1, (1.10) and (1.11)]).
3 Proof of (1.6)
The proof of (1.6) is similar to the proof of (1.3). First, we need a lemma.
Lemma 3.1. Let
$0< b<4d$
. Then
$$ \begin{align} A_{b,d}&=\sum_{m,n=-\infty}^\infty q^{2(bm^2+bmn+dn^2)} = \vartheta_3(q^{2b})\vartheta_3(q^{2(4d-b)})+\vartheta_2(q^{2b})\vartheta_2(q^{2(4d-b)}), \end{align} $$
$$ \begin{align}\ B_{b,d}&=\sum_{m,n=-\infty}^\infty (-1)^{m-n}q^{bm^2+bmn+dn^2} = \vartheta_4(q^{b})\vartheta_4(q^{4d-b})\qquad\qquad\qquad\qquad \end{align} $$
and
$$ \begin{align} C_{b,d}&=\sum_{m,n=-\infty}^\infty q^{2(b(m+1/2)^2+b(m+1/2)n+dn^2)}=\vartheta_2(q^{2b})\vartheta_3(q^{2(4d-b)})+ \vartheta_3(q^{2b})\vartheta_2(q^{2(4d-b)}). \end{align} $$
Proof. The proof of (3.1) follows by writing
$A_{b,d}$
as
$$ \begin{align*} A_{b,d} = \sum_{m,n=-\infty}^\infty q^{2b(m+n/2)^2+n^2(4d-b)/2}. \end{align*} $$
Splitting the sum into two sums with one summing over even integers
$n=2\ell $
and the other summing over odd integers
$n=2\ell +1$
, we find that
$$ \begin{align*} A_{b,d} &= \sum_{m,\ell=-\infty}^\infty q^{2b(m+\ell)^2+2\ell^2(4d-b)}+ \sum_{m,\ell=-\infty}^\infty q^{2b(m+\ell+1/2)^2+2(\ell+1/2)^2(4d-b)}\\ &=\vartheta_3(q^{2b})\vartheta_3(q^{2(4d-b)})+\vartheta_2(q^{2b})\vartheta_2(q^{2(4d-b)}), \end{align*} $$
and this completes the proof of (3.1). Next, write
$B_{b,d}$
as
$$ \begin{align*}B_{b,d} = \sum_{m,n=-\infty}^\infty (-1)^{m-n} q^{b(m+n/2)^2+n^2(4d-b)/4}.\end{align*} $$
Splitting the sum into two sums with one summing over even integers
$n=2\ell $
and the other summing over odd integers
$n=2\ell +1$
and using (2.5), we find that
$$ \begin{align*} B_{b,d} &= \sum_{m,\ell=-\infty}^\infty (-1)^m q^{2b(m+\ell)^2+2\ell^2(4d-b)}+ \sum_{m,\ell=-\infty}^\infty q^{2b(m+\ell+1/2)^2+2(\ell+1/2)^2(4d-b)}\\ &=\sum_{m,\ell=-\infty}^\infty (-1)^\ell q^{(4d-b)\ell^2}\sum_{m=-\infty}^\infty (-1)^{m+\ell} q^{b(m+\ell)^2}\\ &=\vartheta_4(q^{4d-b})\vartheta_4(q^b), \end{align*} $$
and (3.2) follows. Finally, to prove (3.3), write
$$ \begin{align*} C_{b,d} = \sum_{m,n=-\infty}^\infty q^{2 b(m+1/2+n/2)^2+2n^2(4d-b)/4}. \end{align*} $$
Splitting the sum into two sums with one summing over even integers
$n=2\ell $
and the other summing over odd integers
$n=2\ell +1$
, we deduce that
$$ \begin{align*} C_{b,d} &= \sum_{m,\ell=-\infty}^\infty q^{2b(m+\ell+1/2)^2+2(2\ell)^2(4d-b)/4}+ \sum_{m,\ell=-\infty}^\infty q^{2b(m+\ell+1)^2+2(2\ell+1)^2(4d-b)/4}\\ &=\vartheta_2(q^{2b})\vartheta_3(q^{8d-2b})+\vartheta_3(q^{2b})\vartheta_2(q^{8d-2b}), \end{align*} $$
and the proof of (3.3) is complete.
To complete the proof of (1.6), we note that
$$ \begin{align*}A_{b,d}-C_{b,d} = (\vartheta_3(q^{2b})-\vartheta_2(q^{2b})) (\vartheta_3(q^{8d-2b})-\vartheta_2(q^{8d-2b}))\end{align*} $$
and
$$ \begin{align*}A_{b,d}+C_{b,d} = (\vartheta_3(q^{2b})+\vartheta_2(q^{2b})) (\vartheta_3(q^{8d-2b})+\vartheta_2(q^{8d-2b})).\end{align*} $$
But it is immediate that
$$ \begin{align*}\vartheta_3(q^4)-\vartheta_2(q^4) = \vartheta_4(q)\end{align*} $$
and
$$ \begin{align*}\vartheta_3(q^4)+\vartheta_2(q^4) = \vartheta_3(q).\end{align*} $$
Therefore,
$$ \begin{align*}(\vartheta_3(q^4)-\vartheta_2(q^4))(\vartheta_3(q^4)+\vartheta_2(q^4))= \vartheta_4(q)\vartheta_3(q)=\vartheta_4^2(q^2),\end{align*} $$
where the last equality follows from [Reference Borwein and Borwein2, page 34]. Therefore,
$$ \begin{align*} A_{b,d}^2-C_{b,d}^2& = (\vartheta_3(q^{2b})-\vartheta_2(q^{2b})) (\vartheta_3(q^{8d-2b})-\vartheta_2(q^{8d-2b}))\\ &\quad\times (\vartheta_3(q^{2b})+\vartheta_2(q^{2b})) (\vartheta_3(q^{8d-2b})+\vartheta_2(q^{8d-2b}))\\ &=\vartheta_4^2(q^b)\vartheta_4^2(q^{4d-b})=B_{b,d}^2, \end{align*} $$
and the proof of (1.6) is complete.
4 Concluding remarks
We have found infinitely many solutions to
$X^2+Y^2=Z^2$
, where
$X,Y$
and Z are theta series of weight one. The Borweins’ identity states that
$$ \begin{align} \bigg(\sum_{m,n=-\infty}^\infty q^{m^2+mn+n^2}\bigg)^3 &=\bigg(\sum_{m,n=-\infty}^\infty \omega^{m-n}q^{m^2+mn+n^2}\bigg)^3 \notag \\ &\quad +\bigg(\sum_{m,n=-\infty}^\infty q^{(m+1/3)^2+(m+1/3)(n+1/3)+(n+1/3)^2}\bigg)^3, \end{align} $$
where
$\omega =e^{2\pi i/3}.$
This is the only example of a solution to
$X^3+Y^3=Z^3$
with X, Y and Z being theta series of weight one. Are there infinitely many solutions to
$X^3+Y^3=Z^3$
, where
$X,Y$
and Z are theta series of weight one, apart from (4.1)? This appears to be an interesting question.
Open access
