No CrossRef data available.
Published online by Cambridge University Press: 13 September 2019
Given a finite group 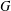 $G$, define the minimal degree
$G$, define the minimal degree 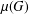 $\unicode[STIX]{x1D707}(G)$ of
$\unicode[STIX]{x1D707}(G)$ of 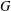 $G$ to be the least
$G$ to be the least  $n$ such that
$n$ such that 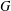 $G$ embeds into
$G$ embeds into 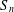 $S_{n}$. We call
$S_{n}$. We call 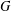 $G$ exceptional if there is some
$G$ exceptional if there is some 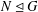 $N\unlhd G$ with
$N\unlhd G$ with 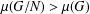 $\unicode[STIX]{x1D707}(G/N)>\unicode[STIX]{x1D707}(G)$, in which case we call
$\unicode[STIX]{x1D707}(G/N)>\unicode[STIX]{x1D707}(G)$, in which case we call 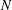 $N$ distinguished. We prove here that a subgroup with no abelian composition factors is not distinguished.
$N$ distinguished. We prove here that a subgroup with no abelian composition factors is not distinguished.
This work was supported by the Engineering and Physical Sciences Research Council.