Hostname: page-component-7dd5485656-wxk4p Total loading time: 0 Render date: 2025-10-28T09:48:34.919Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE LOWEST ZERO OF THE DEDEKIND ZETA FUNCTION

Part of: Algebraic number theory: global fields Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  22 October 2024

SUSHANT KALA Open the ORCID record for SUSHANT KALA [Opens in a new window]
SUSHANT KALA*
Affiliation:
Department of Mathematics, Institute of Mathematical Sciences (HBNI), CIT Campus, IV Cross Road, Chennai 600113, India
*
e-mail: sushant@imsc.res.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 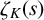$\zeta _K(s)$ denote the Dedekind zeta-function associated to a number field K. We give an effective upper bound for the height of the first nontrivial zero other than 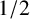$1/2$ of $\zeta _K(s)$ under the generalised Riemann hypothesis. This is a refinement of the earlier bound obtained by Sami [‘Majoration du premier zéro de la fonction zêta de Dedekind’, Acta Arith. 99(1) (2000), 61–65].

Keywords

Dedekind zeta functionlow-lying zerosgeneralised Riemann hypothesisexplicit formula

MSC classification

Primary: 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses
Secondary: 11R42: Zeta functions and $L$-functions of number fields

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 111 , Issue 3 , June 2025 , pp. 460 - 468
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Armitage, J. V., ‘Zeta functions with a zero at $s=\frac{1}{2}$ ’, Invent. Math. 15 (1971/72), 199–205.CrossRefGoogle Scholar
Bllaca, K. H., ‘On properties of certain special zeros of functions in the Selberg class’, Bull. Malays. Math. Sci. Soc. 41 (2018), 1429–1448.CrossRefGoogle Scholar
Carneiro, E., Chandee, V. and Milinovich, M. B., ‘A note on the zeros of zeta and $L$ -functions’, Math. Z. 281 (2015), 315–332.CrossRefGoogle Scholar
Dixit, A. B. and Kala, S., ‘Lower bound on height of algebraic numbers and low lying zeros of the Dedekind zeta-function’, Preprint, 2023, arXiv:2309.15872.Google Scholar
Hoffstein, J., ‘Some results related to minimal discriminants’, in: Number Theory, Carbondale 1979: Proceedings of the Southern Illinois Number Theory Conference, Lecture Notes in Mathematics, 751 (ed. Nathanson, M. B.) (Springer, Berlin–Heidelberg–New York, 1979), 185–194.CrossRefGoogle Scholar
Mestre, J.-F., ‘Formules explicites et minorations de conducteurs de variétés algébriques’, Compos. Math. 58 (1986), 209–232.Google Scholar
Neugebauer, A., On Zeros of Zeta Functions in Low Rectangles in the Critical Strip, PhD Thesis (A. Mickiewicz University, Poznań, Poland, 1985).Google Scholar
Neugebauer, A., ‘On the zeros of the Dedekind zeta function near the real axis’, Funct. Approx. Comment. Math. 16 (1988), 165–167.Google Scholar
Odlyzko, A. M., ‘Bounds for discriminants and related estimates for class numbers, regulators and zeros of zeta functions: a survey of recent results’, J. Théor. Nombres Bordeaux 2 (1990), 119–141.CrossRefGoogle Scholar
Poitou, G., ‘Sur les petits discriminants’, Séminaire Delange–Pisot–Poitou, Théor. Nombres 18(1) (1977), Exp. 6.Google Scholar
Rosser, J. B. and Schoenfeld, L., ‘Approximate formulas for some functions of prime numbers’. Illinois J. Math. 6 (1962), 64–94.CrossRefGoogle Scholar
Sami, O., ‘Majoration du premier zéro de la fonction zêta de Dedekind’, Acta Arith. 99(1) (2000), 61–65.Google Scholar
Soundararajan, K., ‘Nonvanishing of quadratic Dirichlet $L$ -functions at $s=1/2$ ’, Ann. of Math. (2) 152(2) (2000), 447–488.CrossRefGoogle Scholar
Tollis, E., ‘Zeros of Dedekind zeta functions in the critical strip’, Math. Comp. 66 (1997), 1295–1321.CrossRefGoogle Scholar
Tsfasman, M. A. and Vlăduţ, S. G., ‘Infinite global fields and the generalized Brauer–Siegel theorem’, Mosc. Math. J. 2(2) (2002), 329–402.CrossRefGoogle Scholar