Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-10T10:14:52.445Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE EULER CHARACTERISTICS OF SIGNED SELMER GROUPS

Part of: Algebraic number theory: local and $p$-adic fields Algebraic number theory: global fields Arithmetic algebraic geometry

Published online by Cambridge University Press:  09 July 2019

SUMAN AHMED Open the ORCID record for SUMAN AHMED [Opens in a new window]  and
MENG FAI LIM Open the ORCID record for MENG FAI LIM [Opens in a new window]
SUMAN AHMED
Affiliation:
School of Mathematics and Statistics, Central China Normal University, Wuhan, 430079, PR China email npur.suman@gmail.com
MENG FAI LIM*
Affiliation:
School of Mathematics and Statistics and Hubei Key Laboratory of Mathematical Sciences, Central China Normal University, Wuhan, 430079, PR China email limmf@mail.ccnu.edu.cn
*
✉limmf@mail.ccnu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 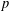$p$ be an odd prime number and 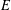$E$ an elliptic curve defined over a number field 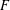$F$ with good reduction at every prime of 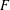$F$ above 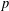$p$. We compute the Euler characteristics of the signed Selmer groups of 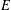$E$ over the cyclotomic 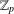$\mathbb{Z}_{p}$-extension. The novelty of our result is that we allow the elliptic curve to have mixed reduction types for primes above 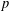$p$ and mixed signs in the definition of the signed Selmer groups.

Keywords

Euler characteristicssigned Selmer groups

MSC classification

Primary: 11R23: Iwasawa theory
Secondary: 11G05: Elliptic curves over global fields 11S25: Galois cohomology
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 2 , April 2020 , pp. 238 - 246
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

M. F. Lim is supported by the National Natural Science Foundation of China under Grant Nos. 11550110172 and 11771164.

References

Büyükboduk, K. and Lei, A., ‘Integral Iwasawa theory of Galois representations for non-ordinary primes’, Math. Z. 286 (2017), 361–398.Google Scholar
Coates, J. and Sujatha, R., Galois Cohomology of Elliptic Curves, 2nd edn, Tata Institute of Fundamental Research Lectures on Mathematics, 88 (Narosa, New Delhi–Mumbai, 2010).Google Scholar
Greenberg, R., ‘Iwasawa theory for p-adic representations’, in: Algebraic Number Theory—in Honor of K. Iwasawa, Advanced Studies in Pure Mathematics, 17 (eds. Coates, J., Greenberg, R., Mazur, B. and Satake, I.) (Kinokuniya–Mathematical Society of Japan, Tokyo, 1989), 97–137.Google Scholar
Greenberg, R., ‘Trivial zeros of p-adic L-functions’, in: p-adic Monodromy and the Birch and Swinnerton-Dyer Conjecture (Boston, MA, 1991), Contemporary Mathematics, 165 (American Mathematical Society, Providence, RI, 1994), 149–174.Google Scholar
Greenberg, R., ‘Iwasawa theory for elliptic curves’, in: Arithmetic Theory of Elliptic Curves (Cetraro, 1997), Lecture Notes in Mathematics, 1716 (ed. Viola, C.) (Springer, Berlin, 1999), 51–144.Google Scholar
Kato, K., ‘p-adic Hodge theory and values of zeta functions of modular forms’, in: Cohomologies p-adiques et applications arithmétiques. III, Astérisque, 295 (Société Mathématique de France, Paris, 2004), 117–290.Google Scholar
Kim, B. D., ‘The parity conjecture for elliptic curves at supersingular reduction primes’, Compos. Math. 143 (2007), 47–72.Google Scholar
Kim, B. D., ‘The plus/minus Selmer groups for supersingular primes’, J. Aust. Math. Soc. 95(2) (2013), 189–200.Google Scholar
Kitajima, T. and Otsuki, R., ‘On the plus and the minus Selmer groups for elliptic curves at supersingular primes’, Tokyo J. Math. 41(1) (2018), 273–303.Google Scholar
Kobayashi, S., ‘Iwasawa theory for elliptic curves at supersingular primes’, Invent. Math. 152(1) (2003), 1–36.Google Scholar
Lei, A. and Sujatha, R., ‘On Selmer groups in the supersingular reduction case’, Preprint.Google Scholar
Mattuck, A., ‘Abelian varieties over p-adic ground fields’, Ann. of Math. (2) 62 (1955), 92–119.Google Scholar
Mazur, B., ‘Rational points of abelian varieties with values in towers of number fields’, Invent. Math. 18 (1972), 183–266.Google Scholar
Mazur, B., Tate, J. and Teitelbaum, J., ‘On p-adic analogues of the conjectures of Birch and Swinnerton-Dyer’, Invent. Math. 84 (1986), 1–48.Google Scholar
Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of Number Fields, 2nd edn, Grundlehren der Mathematischen Wissenschaften, 323 (Springer, Berlin, 2008).Google Scholar
Perrin-Riou, B., ‘Arithmétique des courbes elliptiques et theórie d’Iwasawa’, Mém. Soc. Math. Fr. 17 (1984), 1–129.Google Scholar
Schneider, P., ‘Iwasawa L-functions of varieties over algebraic number fields. A first approach’, Invent. Math. 71 (1983), 251–293.Google Scholar