No CrossRef data available.
Article contents
ON THE CENTRAL KERNEL OF A GROUP
Published online by Cambridge University Press: 13 October 2022
Abstract
The central kernel 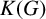 $K(G)$ of a group G is the (characteristic) subgroup consisting of all elements
$K(G)$ of a group G is the (characteristic) subgroup consisting of all elements  $x\in G$ such that
$x\in G$ such that 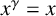 $x^{\gamma }=x$ for every central automorphism
$x^{\gamma }=x$ for every central automorphism 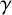 $\gamma $ of G. We prove that if G is a finite-by-nilpotent group whose central kernel has finite index, then the full automorphism group
$\gamma $ of G. We prove that if G is a finite-by-nilpotent group whose central kernel has finite index, then the full automorphism group 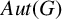 $Aut(G)$ of G is finite. Some applications of this result are given.
$Aut(G)$ of G is finite. Some applications of this result are given.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 108 , Issue 2 , October 2023 , pp. 283 - 289
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The author is a member of GNSAGA-INdAM and ADV-AGTA. This work was carried out within the ‘VALERE: VAnviteLli pEr la RicErca’ project.
References
Alperin, J. L., ‘Groups with finitely many automorphisms’, Pacific J. Math. 12 (1962), 1–5.10.2140/pjm.1962.12.1CrossRefGoogle Scholar
Baer, R., ‘Endlichkeitskriterien für Kommutatorgruppen’, Math. Ann. 124 (1952), 161–177.10.1007/BF01343558CrossRefGoogle Scholar
Brescia, M. and Russo, A., ‘On cyclic automorphisms of a group’, J. Algebra Appl. 20(10) (2021), Article no. 2150183.10.1142/S0219498821501838CrossRefGoogle Scholar
Catino, F., de Giovanni, F. and Miccoli, M. M., ‘On fixed points of central automorphisms of finite-by-nilpotent groups’, J. Algebra 409 (2014), 1–10.10.1016/j.jalgebra.2014.03.031CrossRefGoogle Scholar
Cooper, C. D. H., ‘Power automorphisms of a group’, Math. Z. 107 (1968), 335–356.10.1007/BF01110066CrossRefGoogle Scholar
de Giovanni, F., Newell, M. L. and Russo, A., ‘A note on fixed points of automorphisms of infinite groups’, Int. J. Group Theory 3(4) (2014), 57–61.Google Scholar
de Giovanni, F., Newell, M. L. and Russo, A., ‘On a class of normal endomorphisms of groups’, J. Algebra Appl. 13(1) (2014), Article no. 135001.Google Scholar
Haimo, F., ‘Normal automorphisms and their fixed points’, Trans. Amer. Math. Soc. 78 (1955), 150–167.10.1090/S0002-9947-1955-0067894-0CrossRefGoogle Scholar
Hegarty, P., ‘The absolute centre of a group’, J. Algebra 169 (1994), 929–935.10.1006/jabr.1994.1318CrossRefGoogle Scholar
Nagrebeckiĭ, V. T., ‘On the periodic part of a group with finite number of automorphisms’, Soviet Math. Dokl. 13 (1972), 953–956.Google Scholar
Pettet, M. R., ‘Central automorphisms of periodic groups’, Arch. Math. (Basel) 51 (1988), 20–33.10.1007/BF01194150CrossRefGoogle Scholar
Robinson, D. J. S., A Course in the Theory of Groups (Springer-Verlag, Berlin, 1982).10.1007/978-1-4684-0128-8CrossRefGoogle Scholar
Stammbach, U., Homology in Group Theory (Springer-Verlag, Berlin, 1973).10.1007/BFb0067177CrossRefGoogle Scholar


