No CrossRef data available.
Article contents
ON MINIMAL RESTRICTED ASYMPTOTIC BASES
Part of:
Sequences and sets
Published online by Cambridge University Press: 06 October 2022
Abstract
Let 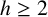 $h \geq 2$ be a positive integer. We introduce the concept of minimal restricted asymptotic bases and obtain some examples of minimal restricted asymptotic bases of order h.
$h \geq 2$ be a positive integer. We introduce the concept of minimal restricted asymptotic bases and obtain some examples of minimal restricted asymptotic bases of order h.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This work was supported by the National Natural Science Foundation of China (Grant No. 11971033), Top Talents Project of Anhui Department of Education (Grant No. gxbjZD05) and Key Project of Anhui Department of Education (Grant No. KJ2021A0099).
References
Alladi, K. and Krantz, S., ‘Reflections on Paul Erdős on his birth centenary’, Notices Amer. Math. Soc. 62 (2015), 121–143.Google Scholar
Chen, Y. G. and Tang, M., ‘On a problem of Nathanson’, Acta Arith. 185 (2018), 275–280.10.4064/aa171031-26-4CrossRefGoogle Scholar
Jańczak, M. and Schoen, T., ‘Dense minimal asymptotic bases of order two’, J. Number Theory 130 (2010), 580–585.10.1016/j.jnt.2009.09.010CrossRefGoogle Scholar
Nathanson, M. B., ‘Minimal bases and maximal nonbases in additive number theory’, J. Number Theory 6 (1974), 324–333.10.1016/0022-314X(74)90028-6CrossRefGoogle Scholar
Nathanson, M. B., ‘Cassels bases’, in: Additive Number Theory (eds. Chudnovsky, D. and Chudnovsky, G.) (Springer, New York, 2010), 259–285.10.1007/978-0-387-68361-4_19CrossRefGoogle Scholar
Nathanson, M. B., ‘A new class of minimal asymptotic bases’, Preprint, 2022, arXiv:2006.14562v2.CrossRefGoogle Scholar
Sun, C. F., ‘On a problem of Nathanson on minimal asymptotic bases’, J. Number Theory 218 (2021), 152–160.10.1016/j.jnt.2020.07.014CrossRefGoogle Scholar
Sun, C. F. and Tao, T. T., ‘On
 $g$
-adic minimal asymptotic bases of order
$g$
-adic minimal asymptotic bases of order
 $h$
’, Int. J. Number Theory 15 (2019), 389–406.10.1142/S1793042119500209CrossRefGoogle Scholar
$h$
’, Int. J. Number Theory 15 (2019), 389–406.10.1142/S1793042119500209CrossRefGoogle Scholar


