Hostname: page-component-857557d7f7-qdphv Total loading time: 0 Render date: 2025-12-12T09:22:01.522Z Has data issue: false hasContentIssue false
  • English
  • Français

A NEW PROOF OF THE SINGULAR CONTINUITY OF THE MINKOWSKI $?$-FUNCTION

Part of: Basic linear algebra Stochastic analysis Real functions

Published online by Cambridge University Press:  04 December 2025

MICHAEL COONS Open the ORCID record for MICHAEL COONS [Opens in a new window] ,
SAMUEL COYLE Open the ORCID record for SAMUEL COYLE [Opens in a new window] ,
ARI PINCUS KAZMAR ,
ADAM STOUT  and
DYLAN WOOD
MICHAEL COONS*
Affiliation:
Department of Mathematics and Statistics, California State University, 400 West First Street, Chico, California, USA
SAMUEL COYLE
Affiliation:
School of Mathematics, University of Minnesota, 206 Church Street SE, Minneapolis, Minnesota, USA e-mail: coyle158@umn.edu
ARI PINCUS KAZMAR
Affiliation:
Department of Mathematics, Statistics and Computer Science, Macalester College, 1600 Grand Avenue, St. Paul, Minnesota, USA e-mail: aripincuskazmar@gmail.com
ADAM STOUT
Affiliation:
Department of Mathematics and Statistics, California State University, 400 West First Street, Chico, California, USA e-mail: astout@csuchico.edu
DYLAN WOOD
Affiliation:
Department of Mathematics and Statistics, California State University, 400 West First Street, Chico, California, USA e-mail: drwood@csuchico.edu
*
e-mail: mjcoons@csuchico.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We give a new proof of the singular continuity of Minkowski’s 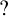$?$-function. Our proof follows by showing that the maximal Lyapunov exponent of a specific pair of $3\times 3$ nonnegative integer matrices related to Stern’s diatomic sequence is strictly greater than $\log 2$.

Keywords

singular functionLyapunov exponentMinkowski ?-functionStern’s sequence

MSC classification

Primary: 26A30: Singular functions, Cantor functions, functions with other special properties
Secondary: 60H25: Random operators and equations 15A60: Norms of matrices, numerical range, applications of functional analysis to matrix theory

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 6
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was supported by the National Science Foundation under grant DMS-2244020. The first author was supported by a David W. and Helen E. F. Lantis Endowment.

References

Allouche, J.-P. and Shallit, J., ‘The ring of $k$ -regular sequences’, Theoret. Comput. Sci. 98 (1992), 163–197.10.1016/0304-3975(92)90001-VCrossRefGoogle Scholar
Allouche, J.-P. and Shallit, J., Automatic Sequences (Cambridge University Press, Cambridge, 2003).10.1017/CBO9780511546563CrossRefGoogle Scholar
Berg, L. and Krüppel, M., ‘De Rham’s singular function and related functions’, Z. Anal. Anwend. 19(1) (2000), 227–237.10.4171/zaa/947CrossRefGoogle Scholar
Brocot, A., ‘Calcul des rouages par approximation, nouvelle méthode’, Revue Chronométrique 3 (1861), 186–194.Google Scholar
Coons, M., Evans, J., Gohlke, P. and Mañibo, N., ‘Spectral theory of regular sequences: parametrisation and spectral classification’, Preprint, 2023, arXiv:2307.15185.10.4171/dm/880CrossRefGoogle Scholar
Coons, M., Evans, J., Groth, Z. and Mañibo, N., ‘Zaremba, Salem and the fractal nature of ghost distributions’, Bull. Aust. Math. Soc. 107(3) (2023), 374–389.10.1017/S0004972722001046CrossRefGoogle Scholar
Coons, M., Evans, J. and Mañibo, N., ‘Spectral theory of regular sequences’, Doc. Math. 27 (2022), 629–653.10.4171/dm/880CrossRefGoogle Scholar
Dovgoshei, A. A. and Martio, O., ‘Mutually singular functions and the calculation of the lengths of curves’, Izv. Ross. Akad. Nauk Ser. Mat. 70(4) (2006), 53–76; translation in Izv. Math. 70(40) (2006), 693–716.Google Scholar
Dushistova, A. A., Kan, I. D. and Moshchevitin, N. G., ‘Differentiability of the Minkowski question mark function’, J. Math. Anal. Appl. 401(2) (2013), 774–794.10.1016/j.jmaa.2012.12.058CrossRefGoogle Scholar
Minkowski, H., ‘Zur Geometrie der Zahlen’, in: Verhandlungen des dritten Intern. Math.-Kongr. Heidelberg, 1904 (ed. A. Krazer) (Teubner, Berlin, 1905), 164–173.Google Scholar
Northshield, S., ‘Stern’s diatomic sequence $0,1,1,2,1,3,2,3,1,4,\dots$ ’, Amer. Math. Monthly 117(7) (2010), 581–598.10.4169/000298910x496714CrossRefGoogle Scholar
Protasov, V. Yu., ‘Asymptotics of products of nonnegative random matrices’, Funktsional. Anal. i Prilozhen. 47(2) (2013), 68–79; translation in Funct. Anal. Appl. 47(2) (2013), 138–147.10.1007/s10688-013-0018-8CrossRefGoogle Scholar
Protasov, V. Yu. and Jungers, R. M., ‘Lower and upper bounds for the largest Lyapunov exponent of matrices’, Linear Algebra Appl. 438(11) (2013), 4448–4468.10.1016/j.laa.2013.01.027CrossRefGoogle Scholar
Salem, R., ‘On some singular monotonic functions which are strictly increasing’, Trans. Amer. Math. Soc. 53 (1943), 427–439.10.1090/S0002-9947-1943-0007929-6CrossRefGoogle Scholar
Stern, M. A., ‘Ueber eine zahlentheoretische Funktion’, J. reine angew. Math. 55 (1858), 193–220.Google Scholar