Article contents
A RECONSTRUCTION OF STEEL’S MULTIVERSE PROJECT
Published online by Cambridge University Press: 11 June 2020
Abstract
This paper reconstructs Steel’s multiverse project in his ‘Gödel’s program’ (Steel, 2014), first by comparing it to those of Hamkins (2012) and Woodin (2011), then by detailed analysis what’s presented in Steel’s brief text. In particular, we reconstruct his notion of a ‘natural’ theory, describe his multiverse axioms and his translation function, and assess the resulting status of the Continuum Hypothesis. In the end, we reconceptualize the defect that Steel thinks 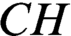 $CH$ might suffer from and isolate what it would take to remove it while working within his framework. As our goal is to present as coherent and compelling a philosophical and mathematical story as we can, we allow ourselves to augment Steel’s story in places (e.g., in the treatment of Amalgamation) and to depart from it in others (e.g., the removal of ‘meaning’ from the account). The relevant mathematics is laid out in the appendices.
$CH$ might suffer from and isolate what it would take to remove it while working within his framework. As our goal is to present as coherent and compelling a philosophical and mathematical story as we can, we allow ourselves to augment Steel’s story in places (e.g., in the treatment of Amalgamation) and to depart from it in others (e.g., the removal of ‘meaning’ from the account). The relevant mathematics is laid out in the appendices.
Keywords
Information
- Type
- Articles
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 22
- Cited by

