No CrossRef data available.
Published online by Cambridge University Press: 16 January 2023
Locality is a property of logics, whose origins lie in the works of Hanf and Gaifman, having their utility in the context of finite model theory. Such a property is quite useful in proofs of inexpressibility, but it is also useful in establishing normal forms for logical formulas. There are generally two forms of locality: (i’) if two structures
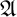 $\mathfrak {A}$
and
$\mathfrak {A}$
and
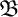 $\mathfrak {B}$
realize the same multiset of types of neighborhoods of radius d, then they agree on a given sentence
$\mathfrak {B}$
realize the same multiset of types of neighborhoods of radius d, then they agree on a given sentence
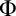 $\Phi $
. Here d depends only on
$\Phi $
. Here d depends only on
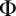 $\Phi $
; (ii’) if the d-neighborhoods of two tuples
$\Phi $
; (ii’) if the d-neighborhoods of two tuples
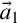 $\vec {a}_1$
and
$\vec {a}_1$
and
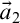 $\vec {a}_2$
in a structure
$\vec {a}_2$
in a structure
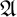 $\mathfrak {A}$
are isomorphic, then
$\mathfrak {A}$
are isomorphic, then
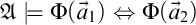 $\mathfrak {A} \models \Phi (\vec {a}_1) \Leftrightarrow \Phi (\vec {a}_2)$
. Again, d depends on
$\mathfrak {A} \models \Phi (\vec {a}_1) \Leftrightarrow \Phi (\vec {a}_2)$
. Again, d depends on
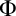 $\Phi $
, and not on
$\Phi $
, and not on
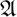 $\mathfrak {A}$
. Form (i’) originated from Hanf’s works. Form (ii’) came from Gaifman’s theorem. There is no doubt about the usefulness of the notion of locality, which as seen applies to a huge number of situations. However, there is a deficiency in such a notion: all versions of the notion of locality refer to isomorphism of neighborhoods, which is a fairly strong property. For example, where structures simply do not have sufficient isomorphic neighborhoods, versions of the notion of locality obviously cannot be applied. So the question that immediately arises is: would it be possible to weaken such a condition and maintain Hanf/Gaifman-localities? Arenas, Barceló, and Libkin establish a new condition for the notions of locality, weakening the requirement that neighborhoods should be isomorphic, establishing only the condition that they must be indistinguishable in a given logic. That is, instead of requiring
$\mathfrak {A}$
. Form (i’) originated from Hanf’s works. Form (ii’) came from Gaifman’s theorem. There is no doubt about the usefulness of the notion of locality, which as seen applies to a huge number of situations. However, there is a deficiency in such a notion: all versions of the notion of locality refer to isomorphism of neighborhoods, which is a fairly strong property. For example, where structures simply do not have sufficient isomorphic neighborhoods, versions of the notion of locality obviously cannot be applied. So the question that immediately arises is: would it be possible to weaken such a condition and maintain Hanf/Gaifman-localities? Arenas, Barceló, and Libkin establish a new condition for the notions of locality, weakening the requirement that neighborhoods should be isomorphic, establishing only the condition that they must be indistinguishable in a given logic. That is, instead of requiring
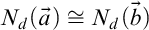 $N_d(\vec {a}) \cong N_d(\vec {b})$
, you should only require
$N_d(\vec {a}) \cong N_d(\vec {b})$
, you should only require
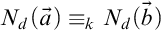 $N_d(\vec {a}) \equiv _k N_d(\vec {b})$
, for some
$N_d(\vec {a}) \equiv _k N_d(\vec {b})$
, for some
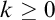 $k \geq 0$
. Using the fact that logical equivalence is often captured by Ehrenfeucht–Fraïssé games, the authors formulate a game-based framework in which logical equivalence-based locality can be defined. Thus, the notion defined by the authors is that of game-based locality. Although quite promising as well as easy to apply, the game-based framework (used to define locality under logical equivalence) has the following problem: if a logic
$k \geq 0$
. Using the fact that logical equivalence is often captured by Ehrenfeucht–Fraïssé games, the authors formulate a game-based framework in which logical equivalence-based locality can be defined. Thus, the notion defined by the authors is that of game-based locality. Although quite promising as well as easy to apply, the game-based framework (used to define locality under logical equivalence) has the following problem: if a logic
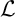 $\mathcal {L}$
is local (Hanf-, or Gaifman-, or weakly) under isomorphisms, and
$\mathcal {L}$
is local (Hanf-, or Gaifman-, or weakly) under isomorphisms, and
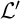 $\mathcal {L}'$
is a sub-logic of
$\mathcal {L}'$
is a sub-logic of
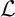 $\mathcal {L}$
, then
$\mathcal {L}$
, then
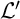 $\mathcal {L}'$
is local as well. The same, however, is not true for game-based locality: properties of games guaranteeing locality need not be preserved if one passes to weaker games. The question that immediately arises is: is it possible to define the notion of locality under logical equivalence without resorting to game-based frameworks? In this thesis, I present a homotopic variation for locality under logical equivalence, namely a Quillen model category-based framework for locality under k-logical equivalence, for every primitive-positive sentence of quantifier-rank k.
$\mathcal {L}'$
is local as well. The same, however, is not true for game-based locality: properties of games guaranteeing locality need not be preserved if one passes to weaker games. The question that immediately arises is: is it possible to define the notion of locality under logical equivalence without resorting to game-based frameworks? In this thesis, I present a homotopic variation for locality under logical equivalence, namely a Quillen model category-based framework for locality under k-logical equivalence, for every primitive-positive sentence of quantifier-rank k.
Abstract prepared by Hendrick Maia.
E-mail: hendrickmaia@gmail.com
URL: http://repositorio.unicamp.br/jspui/handle/REPOSIP/334956
Supervised by Marcelo Esteban Coniglio.