Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fontanella, Laura
and
Hayut, Yair
2016.
Square and Delta reflection.
Annals of Pure and Applied Logic,
Vol. 167,
Issue. 8,
p.
663.
Hayut, Yair
and
Karagila, Asaf
2016.
Restrictions on forcings that change cofinalities.
Archive for Mathematical Logic,
Vol. 55,
Issue. 3-4,
p.
373.
Brodsky, Ari Meir
and
Rinot, Assaf
2017.
A microscopic approach to Souslin-tree constructions, Part I.
Annals of Pure and Applied Logic,
Vol. 168,
Issue. 11,
p.
1949.
RINOT, ASSAF
and
SCHINDLER, RALF
2017.
SQUARE WITH BUILT-IN DIAMOND-PLUS.
The Journal of Symbolic Logic,
Vol. 82,
Issue. 3,
p.
809.
Hayut, Yair
and
Lambie-Hanson, Chris
2017.
Simultaneous stationary reflection and square sequences.
Journal of Mathematical Logic,
Vol. 17,
Issue. 02,
p.
1750010.
Hayut, Yair
2017.
Magidor–Malitz reflection.
Archive for Mathematical Logic,
Vol. 56,
Issue. 3-4,
p.
253.
Larson, J. A.
2017.
In memoriam: James Earl Baumgartner (1943–2011).
Archive for Mathematical Logic,
Vol. 56,
Issue. 7-8,
p.
877.
Rinot, Assaf
2017.
Higher Souslin trees and the GCH, revisited.
Advances in Mathematics,
Vol. 311,
Issue. ,
p.
510.
Cox, Sean
and
Lücke, Philipp
2017.
Characterizing large cardinals in terms of layered posets.
Annals of Pure and Applied Logic,
Vol. 168,
Issue. 5,
p.
1112.
Usuba, Toshimichi
2018.
New combinatorial principle on singular cardinals and normal ideals.
Mathematical Logic Quarterly,
Vol. 64,
Issue. 4-5,
p.
395.
LAMBIE-HANSON, CHRIS
and
LÜCKE, PHILIPP
2018.
SQUARES, ASCENT PATHS, AND CHAIN CONDITIONS.
The Journal of Symbolic Logic,
Vol. 83,
Issue. 04,
p.
1512.
Lambie-Hanson, Chris
and
Rinot, Assaf
2018.
Knaster and friends I: closed colorings and precalibers.
Algebra universalis,
Vol. 79,
Issue. 4,
Lambie-Hanson, Chris
and
Rinot, Assaf
2019.
Reflection on the Coloring and Chromatic Numbers.
Combinatorica,
Vol. 39,
Issue. 1,
p.
165.
Rinot, Assaf
and
Zhang, Jing
2021.
Transformations of the transfinite plane.
Forum of Mathematics, Sigma,
Vol. 9,
Issue. ,
Lambie-Hanson, Chris
and
Rinot, Assaf
2021.
Knaster and friends II: The C-sequence number.
Journal of Mathematical Logic,
Vol. 21,
Issue. 01,
p.
2150002.
Poveda, Alejandro
Rinot, Assaf
and
Sinapova, Dima
2021.
Sigma-Prikry forcing I: The Axioms.
Canadian Journal of Mathematics,
Vol. 73,
Issue. 5,
p.
1205.
Kojman, Menachem
Rinot, Assaf
and
Steprāns, Juris
2022.
Ramsey theory over partitions III: Strongly Luzin sets and partition relations.
Proceedings of the American Mathematical Society,
Vol. 151,
Issue. 1,
p.
369.
Lücke, Philipp
2022.
Strong unfoldability, shrewdness and combinatorial consequences.
Proceedings of the American Mathematical Society,
Vol. 150,
Issue. 9,
p.
4005.
Jarden, Adi
and
Shami, Ziv
2022.
A note on edge colorings and trees.
Mathematical Logic Quarterly,
Vol. 68,
Issue. 4,
p.
447.
Inamdar, Tanmay
and
Rinot, Assaf
2023.
Was Ulam right? I: Basic theory and subnormal ideals.
Topology and its Applications,
Vol. 323,
Issue. ,
p.
108287.
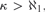 $\kappa> \aleph _1 {\rm{,}}$ the principle □(k) is equivalent to the existence of a certain strong coloring
$\kappa> \aleph _1 {\rm{,}}$ the principle □(k) is equivalent to the existence of a certain strong coloring 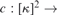 $c\,:\,[k]^2 \, \to $k for which the family of fibers
$c\,:\,[k]^2 \, \to $k for which the family of fibers 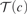 ${\cal T}\left( c \right)$ is a nonspecial κ-Aronszajn tree.
${\cal T}\left( c \right)$ is a nonspecial κ-Aronszajn tree.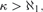 $\kappa> \aleph _1 {\rm{,}}$ then κ is weakly compact in some inner model of ZFC. This provides a partial converse to the fact that if κ is a weakly compact cardinal, then the κ-chain condition is productive.
$\kappa> \aleph _1 {\rm{,}}$ then κ is weakly compact in some inner model of ZFC. This provides a partial converse to the fact that if κ is a weakly compact cardinal, then the κ-chain condition is productive.
