Article contents
An Interpolation Theorem
Published online by Cambridge University Press: 15 January 2014
Abstract
Lyndon's Interpolation Theorem asserts that for any valid implication between two purely relational sentences of first-order logic, there is an interpolant in which each relation symbol appears positively (negatively) only if it appears positively (negatively) in both the antecedent and the succedent of the given implication. We prove a similar, more general interpolation result with the additional requirement that, for some fixed tuple 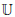 of unary predicates U, all formulae under consideration have all quantifiers explicitly relativised to one of the U. Under this stipulation, existential (universal) quantification over U contributes a positive (negative) occurrence of U.
of unary predicates U, all formulae under consideration have all quantifiers explicitly relativised to one of the U. Under this stipulation, existential (universal) quantification over U contributes a positive (negative) occurrence of U.
It is shown how this single new interpolation theorem, obtained by a canonical and rather elementary model theoretic proof, unifies a number of related results: the classical characterisation theorems concerning extensions (substructures) with those concerning monotonicity, as well as a many-sorted interpolation theorem focusing on positive vs. negative occurrences of predicates and on existentially vs. universally quantified sorts.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2000
References
REFERENCES
- 16
- Cited by

