Systematic reviews with meta-analyses have the potential to play an important role in quantitatively synthesising evidence when numerous studies on a similar topic exist, especially when disagreement persists among those studies. The potential strengths of meta-analysis include (1) increased statistical power for primary outcomes, (2) ability to reach agreement when original studies yield conflicting findings, (3) improving effect size estimates and (4) answering questions not addressed in original trials(Reference Sacks, Berrier and Reitman1). In addition, meta-analyses provide the opportunity to generate hypotheses that can be tested in subsequent original trials. Furthermore, systematic reviews, with or without meta-analysis, often play a major role in guideline development(Reference Zhang, Akl and Schunemann2). In a recent special issue devoted entirely to P values in the American Statistician, Wasserstein et al. suggested that since one study is usually not definitive, meta-analysis is critical to determining the uncertainty in the evidence(Reference Wasserstein, Schirm and Lazar3). Recognising their potential value, the number of systematic reviews, with or without meta-analysis, has increased dramatically over approximately the last 40 years. For example, a simple PubMed search conducted by the authors on 10 May 2019, using the search phrase “systematic review” OR meta-analy* yielded four citations in 1978 v. 31 295 in 2018, the most recent complete year for which data were available. The number of systematic reviews with meta-analyses in the area of nutrition has also increased dramatically over the same time period. A simple PubMed search conducted by the authors on 10 May 2019, using the search phrase (“systematic review” OR meta-analy*) AND (food OR beverages OR diet OR nutrition) yielded one citation in 1978 v. 2743 in 2018, the most recent complete year in which data were available.
Types of systematic reviews
Table 1 lists the different types of systematic reviews with a description provided hereafter.
Table 1. Types of systematic reviews

AD, aggregate data; IPD, individual participant/patient data.
Scoping reviews
While no one universal definition exists, a scoping review may be best defined as a type of research synthesis that aims to ‘map the literature on a particular topic or research area and provide an opportunity to identify key concepts; gaps in the research; and types and sources of evidence to inform practice, policymaking, and research’(Reference Daudt, van Mossel and Scott4). Thus, scoping reviews can be beneficial from both a research and practice perspective. To illustrate its use in the field of nutrition, Amouzandeh et al. recently conducted a scoping review of the validity, reliability and conceptual alignment of food literacy measures for adults(Reference Amouzandeh, Fingland and Vidgen5). The authors concluded that most tools provided a theoretical framework, which is valid and reliable(Reference Amouzandeh, Fingland and Vidgen5). In addition, they believed that their results will assist practitioners in selecting and developing tools for the measurement of food literacy(Reference Amouzandeh, Fingland and Vidgen5). Congruent with other types of reviews, the number of scoping reviews in the field of nutrition is increasing. As an example, a PubMed search conducted on 11 May 2019, using the search phrase (“scoping review” OR “systematic scoping review” OR “scoping report” OR “scope of the evidence” OR “rapid scoping review” OR “structured literature review” OR “scoping project” OR “scoping meta review”) AND (food OR beverages OR diet OR nutrition) demonstrated that the number of citations has increased from one in 1981 to 161 in 2018, the most recent complete year for which data were available. The Preferred Reporting Items for Systematic Reviews and Meta-Analyses extension for Scoping Reviews (PRISMA-ScR) provides an excellent guide, including a checklist, for conducting and reporting a scoping review(Reference Tricco, Lillie and Zarin7). Checklists such as the PRISMA series provide very helpful information to producers, reviewers and consumers (clinicians, guideline developers, etc.) for ensuring that high-quality reviews are conducted. Therefore, the authors advocate that journals require the appropriate checklist when authors submit their manuscript for publication consideration.
Systematic reviews of previous systematic reviews
Given the proliferation of systematic reviews, with or without meta-analysis, on the same topic, there is now a need to assess these previous reviews. As an example of a systematic review of previous systematic reviews (SRPSR) in nutrition, Agostoni et al. recently conducted a SRPSR on the long-term effects of dietary nutrient intake during the first 2 years of life in healthy infants from developed countries(Reference Agostoni, Guz-Mark and Marderfeld8). The overall conclusion of the authors was that a large degree of uncertainty currently exists on the health effects of differences in early nutrition among healthy full-term infants(Reference Agostoni, Guz-Mark and Marderfeld8).
There are at least two important reasons for conducting a SRPSR. First, for those desiring to conduct their own systematic review, with or without meta-analysis, such a review can help justify the conduct of a new or updated review. If an updated or new review is deemed warranted, then this information should be included in the introduction section of the new or updated review. Ideally, this should include reference to a previously published SRPSR. If after searching the literature the authors believe that no previous reviews exist, then this should be stated. The inclusion of this information may be especially important given the recent criticism regarding the publication of redundant reviews on the same topic(Reference Ioannidis9). Fig. 1 depicts a stepwise process suggested by the authors for moving from a SRPSR to one’s own review, details of which can be found elsewhere(Reference Kelley and Kelley10). Briefly, a major decision that needs to be made is whether a new systematic review, with or without meta-analysis, is needed. The Cochrane Collaboration recommends that another systematic review be based on needs and priorities, with consideration of strategic importance, practical aspects as it pertains to organising the review, and impact of another review(11). The Agency for Healthcare Research and Quality in the United States approaches this from a needs-based perspective in which the focus is on stakeholder impact as well as currency and necessity(Reference Shojania, Sampson and Ansari12). A determination is then made to create, archive or continue surveillance(Reference Shojania, Sampson and Ansari12). The Panel for Updating Guidance for Systematic Reviews (PUGS) created a consensus and checklist for when and how to perform another systematic review(Reference Garner, Hopewell and Chandler13). This process includes assessing the currency as well as previous review(s), if any exist, identifying relevant new methods, studies or other information that may justify another review, and assessing the potential impact of another review(Reference Garner, Hopewell and Chandler13). The PUGS guidelines and checklist may be the most suitable method for researchers interested in conducting another systematic review, with or without meta-analysis. Any new reviews should also address an important research question, something that should be explained in the introduction section of the manuscript.
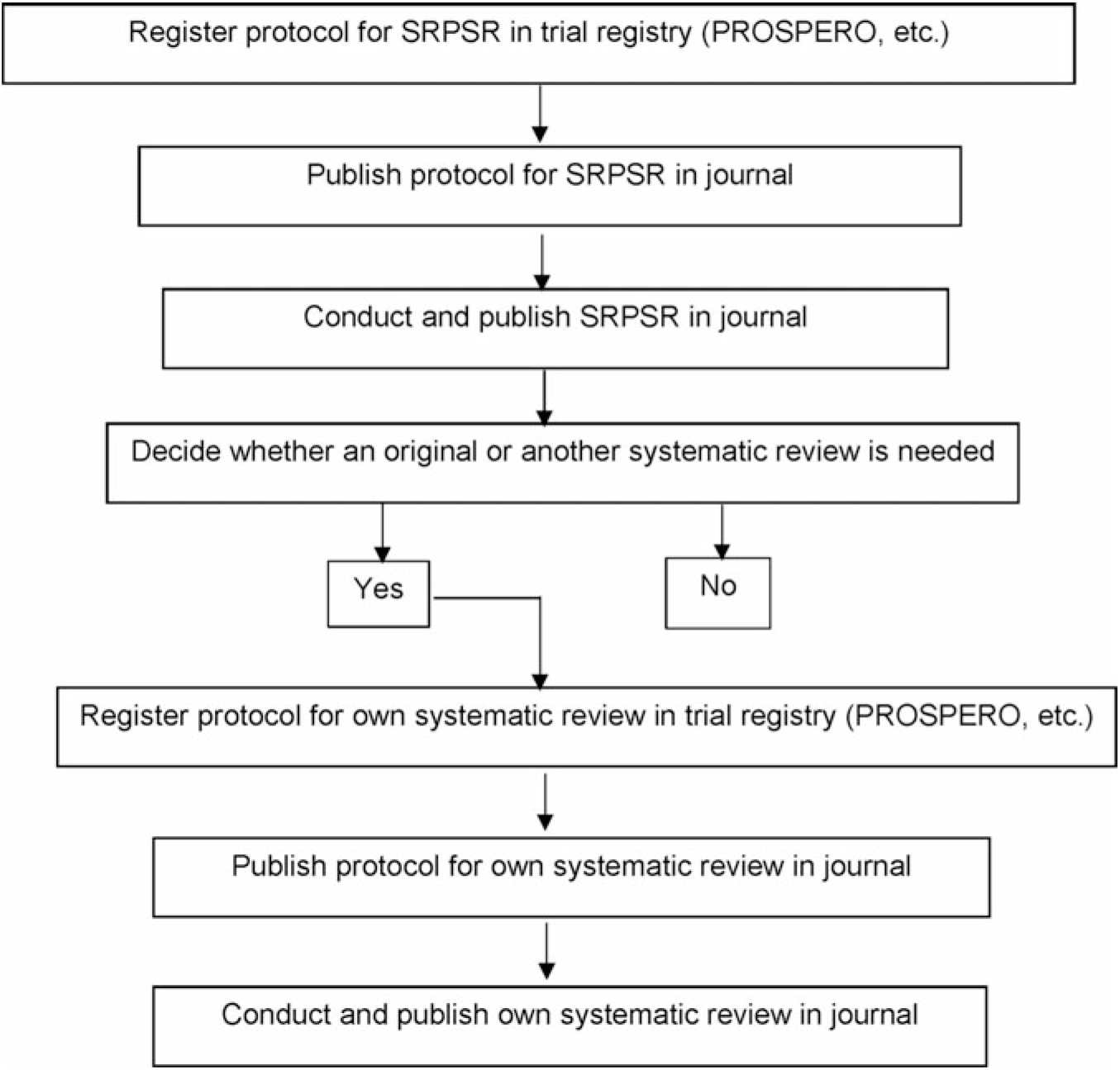
Fig. 1. Suggested stepwise approach for deciding whether a new or updated systematic review, with or without meta-analysis, should be conducted. Adapted from Kelley & Kelley(Reference Kelley and Kelley10). SRPSR, systematic reviews of previous systematic reviews.
A second reason for conducting a SRPSR is that given the large number of reviews of this type on many of the same topics, a need exists to evaluate these in order to provide decision makers (clinicians, guideline developers, policymakers, etc.) with the information they need to make informed choices on the topic of interest. A simple PubMed search conducted by the authors on 10 May 2019, using the search criteria ‘(“systematic review of previous systematic reviews” OR “umbrella review” OR “overview of reviews” OR “review of reviews” OR “summary of systematic reviews” OR “meta-reviews”) AND (food OR beverages OR diet OR nutrition)’ yielded 173 citations associated with nutrition-related SRPSR in 2018, the most recent complete year for which data were available. As part of the conduct of a SRPSR, an evaluation regarding the quality and/or risk of bias of each included systematic review, with or without meta-analysis, should be included. Instruments for assessing such include, but are not limited to, (1) a MeaSurement Tool to Assess systematic Reviews 2(Reference Shea, Reeves and Wells14), (2) Risk of Bias in Systematic Reviews(Reference Whiting, Savovic and Higgins15) (3) Grading of Recommendations, Assessment, Development and Evaluations (GRADE)(Reference Guyatt, Oxman and Akl16) and (4) Quality Assessment of Diagnostic Accuracy Studies 2(Reference Whiting, Rutjes and Westwood17). The importance of SRPSR is supported by a recent thematic series devoted to this topic(Reference McKenzie and Brennan18–Reference Lunny, Brennan and McDonald20). In addition, Ballard & Montgomery also provide methodological guidance, including a four-item checklist, for evaluating a SRPSR(Reference Ballard and Montgomery21). Finally, for the reasons previously given as well as to improve efficiencies and avoid research waste(Reference McKenzie and Brennan18), the authors believe that funding agencies should support high-quality SRPSR. Detailed information regarding SRPSR can be found elsewhere(Reference McKenzie and Brennan18–Reference Pollock, Fernandes and Becker28).
Systematic review without meta-analysis
The Cochrane Collaboration defines a systematic review as a ‘review of a clearly formulated question that uses systematic and explicit methods to identify, select, and critically appraise relevant research, and to collect and analyse data from the studies that are included in the review(Reference Higgins and Green6)’. The key characteristics of a systematic review include (1) clearly stated objectives with predefined eligibility criteria for studies, (2) an explicit, reproducible methodology, (3) a systematic search that attempts to identify all studies that meet the eligibility criteria, (4) an assessment of the validity of the findings of the included studies (risk of bias, etc.) and (5) a systematic presentation and synthesis of the characteristics and findings of the included studies(Reference Higgins and Green6). A systematic review without a meta-analysis is often conducted because the authors feel that the studies are not combinable quantitatively given that they are too different and/or cannot be combined into some type of common metric. This is usually not an easy task since no one study is exactly alike, nor should they be. For example, some people may decide a priori that the studies will be too different to combine quantitatively (apples and oranges) while others may decide that the eligible studies can be combined (fruit salad). If a meta-analysis is not included, then the reason for not doing so should be stated in the research synthesis sub-section of the Methods section of the manuscript. When a meta-analysis is not included, the results are synthesised qualitatively. As an example, Calder et al. conducted a systematic review without meta-analysis with respect to increasing arachidonic acid intake and PUFA status, metabolism and health-related outcomes in humans(Reference Calder, Campoy and Eilander29). Based on twenty-two articles from fourteen randomised controlled trials, the authors concluded that insufficient evidence currently exists to support any recommendation regarding the specific health effects of arachidonic acid intake(Reference Calder, Campoy and Eilander29). The original PRISMA statement provides guidance, including a checklist, for conducting and reporting a systematic review, with or without meta-analysis(Reference Liberati, Altman and Tetzlaff30).
Systematic review with meta-analysis
A systematic review with meta-analysis is similar to a systematic review without a meta-analysis with the exception that the former includes a quantitative synthesis, that is, meta-analysis of the data. Generally, systematic reviews with a meta-analysis consist of the following types: (1) aggregate data (AD) meta-analysis, (2) individual participant/patient data (IPD) meta-analysis, (3) network meta-analysis (NMA), which can be based on either AD or IPD and (4) non-inferiority (NI) meta-analysis (AD or IPD).
Aggregate data meta-analysis. An AD meta-analysis is a quantitative approach in which summary data, for example, sample sizes, means and standard deviations are abstracted for outcomes of interest (kJ consumed, cholesterol intake, etc.) from previously published studies and then pooled for analysis. These are by far the most common types of meta-analyses conducted today and often focus on pairwise comparisons, for example, changes in an intervention v. control group. A simple PubMed search conducted by the authors on 13 May 2019, using the search string (“systematic review” OR meta-analy*) AND (food OR beverages OR diet OR nutrition) NOT (“individual participant data” OR “individual patient data” OR “IPD” OR “systematic review of previous systematic reviews” OR “umbrella review” OR “overview of reviews” OR “review of reviews” OR “summary of systematic reviews” OR “meta-reviews”) yielded a total of one citation in 1978 v. 2557 in 2018, the most recent and complete year in which data were available. As an example of an AD meta-analysis in nutrition, Zhang et al., conducted a systematic review with meta-analysis on the efficacy and safety of iron supplementation in patients with heart failure and iron deficiency(Reference Zhang, Zhang and Du31). Based on nine randomised controlled trials representing 789 patients who received iron therapy, significant improvements were observed for the 6-min walk test and peak maximum oxygen consumption as well as fewer patients being hospitalised for heart failure(Reference Zhang, Zhang and Du31). No associations were found for total re-hospitalisation or mortality(Reference Zhang, Zhang and Du31).
As previously mentioned, the original PRISMA statement provides guidance, including a checklist, for conducting and reporting a systematic review with AD meta-analysis(Reference Liberati, Altman and Tetzlaff30). In addition, recent guidance for conducting systematic reviews and meta-analyses of observational studies in aetiology is also available(Reference Dekkers, Vandenbroucke and Cevallos32) and the Cochrane Handbook provides extensive information on the conduct of systematic reviews with AD meta-analysis(Reference Higgins and Green6).
Individual participant/patient data meta-analysis. An IPD meta-analysis is a systematic review that includes a meta-analysis based on IPD and often comprises a consortium made up of a large number of investigators such as the European Consortium that recently conducted an IPD meta-analysis on vitamin D and mortality(Reference Gaksch, Jorde and Grimnes33). Since de-identified IPD is usually not available in the original studies, it needs to be requested from the author(s). Considered the ‘gold standard’ of meta-analyses, the potential advantages of an IPD meta-analysis, described in detail elsewhere(Reference Riley, Lambert and Abo-Zaid34), include, but are not limited to, ‘standardizing statistical analyses in each study; deriving desired summary results directly, independent of study reporting; checking modelling assumptions; and assessing participant-level effects, interactions and non-linear trends’(Reference Riley35). However, one of the major disadvantages of an IPD meta-analysis is the ability to retrieve original data from study authors, with ranges of 25–100 % reported across different subject areas(Reference Kelley, Kelley and Tran36–Reference Polanin39). As a result, this can lead to an increased risk of bias. While at least one approach has been recommended for integrating both IPD and AD(Reference Riley, Lambert and Staessen40), one is still left with AD from those studies in which IPD cannot be retrieved. A second disadvantage of an IPD v. AD meta-analysis is the increased time and resources associated with such analysis. For example, one study estimated the costs of a previous IPD meta-analysis(Reference Steinberg, Smith and Stroup41) to be eight times greater than an AD meta-analysis(Reference Cooper and Patall42). Finally, several studies have shown a lack of statistically and practically important differences between AD and IPD meta-analyses when an indistinguishable, or nearly indistinguishable, number of studies are included(Reference Steinberg, Smith and Stroup41, Reference Olkin and Sampson43–Reference Tudur Smith, Marcucci and Nolan45). Despite these disadvantages, the number of IPD meta-analyses is increasing, including the field of nutrition. A simple PubMed search conducted by the authors on 13 May 2019, using the search string (“systematic review” OR meta-analy*) AND (food OR beverages OR diet OR nutrition) AND (“individual participant data” OR “individual patient data” OR “IPD”) NOT (“systematic review of previous systematic reviews” OR “umbrella review” OR “overview of reviews” OR “review of reviews” OR “summary of systematic reviews” OR “meta-reviews”) yielded one citation in the year 2002 v. twenty-six in 2018, the most recent year in which complete data were available. As an example in the field of nutrition, Smelt et al. recently conducted an IPD meta-analysis of randomised controlled trials on the effects of vitamin B12 and folic supplementation on routine haematological parameters in adults 60 years of age and older(Reference Smelt, Gussekloo and Bermingham46). The authors concluded that there is currently a lack of evidence to support the effects of supplementation of low concentrations of vitamin B12 and folate on haematological parameters in community-dwelling adults 60 years of age and older(Reference Smelt, Gussekloo and Bermingham46). A set of PRISMA guidelines, including a checklist, for conducting and reporting an IPD meta-analysis (PRISMA-IPD) are available(Reference Stewart, Clarke and Rovers47). Additional details regarding the conduct of an IPD have been reported elsewhere(Reference Higgins and Green6, Reference Riley, Lambert and Abo-Zaid34, Reference Tierney, Vale and Riley48).
Network meta-analysis. A more recent and increasingly used approach, including the field of nutrition(Reference Schwingshackl, Buyken and Chaimani49), is the conduct of a systematic review with NMA, usually in the form of an AD NMA v. IPD NMA. NMA, also known as ‘multiple treatments meta-analysis’ or ‘mixed treatment comparisons meta-analysis’, is a type of meta-analysis that compares at least three treatments and includes both direct (comparing two treatments head to head) and indirect (comparing two treatments via a comparative control group) evidence. One of the major reasons for its increased use is the ability to include multiple treatments in the same analysis, thereby facilitating treatment recommendations. For example, Galaviz et al. recently conducted an NMA on the real-world impact of global diabetes prevention interventions on diabetes incidence, body weight and glucose(Reference Galaviz, Weber and Straus50). The overall conclusion of the authors’ NMA of sixty-three studies was that real-world lifestyle modification strategies can reduce diabetes risk(Reference Galaviz, Weber and Straus50). A simple PubMed search conducted by the authors on 14 May 2019, using the search string (“network meta-analysis” OR “multiple treatments meta-analysis” OR “mixed treatment comparisons meta-analysis”) AND (food OR beverages OR diet OR nutrition) NOT (“systematic review of previous systematic reviews” OR “umbrella review” OR “overview of reviews” OR “review of reviews” OR “summary of systematic reviews” OR “meta-reviews”) yielded one initial citation in the year 2007 v. thirty-three in 2018, the most recent year in which complete data were available. Not surprisingly, NMA is more time and resource intensive than a traditional AD meta-analysis given the large number of treatments that are usually included as well as the inclusion of both direct and indirect evidence. PRISMA guidelines, including a checklist, for conducting and reporting a NMA (PRISMA-NMA) are available(Reference Hutton, Salanti and Caldwell51). Additional details regarding this emerging and important approach have been described elsewhere(Reference Laws, Kendall and Hawkins52–Reference Doi and Barendregt55).
Non-inferiority meta-analysis. The most recent, but still infrequent type of meta-analysis to emerge is a NI meta-analysis. A NI meta-analysis attempts to assess whether a new intervention is no worse than a reference intervention(Reference Brittain, Fay and Follmann56). A major challenge of a NI meta-analysis is the NI margin used(Reference Brittain, Fay and Follmann56). These types of meta-analyses could be based on either AD or IPD and could also take the form of a NMA (AD or IPD)(Reference Schmidli, Wandel and Neuenschwander57). While the authors are not aware of any NI meta-analyses in the field of nutrition, Acuna et al. recently conducted a NI meta-analysis that examined the quality of surgical outcomes using laparoscopic v. open resection for rectal cancer(Reference Acuna, Chesney and Ramjist58). Based on their analysis of fourteen randomised controlled trials, the authors concluded that laparoscopy was non-inferior to open surgery for rectal cancer(Reference Acuna, Chesney and Ramjist58, Reference Acuna, Chesney and Amarasekera59). More detailed information regarding NI meta-analyses can be found elsewhere(Reference Brittain, Fay and Follmann56, Reference Schmidli, Wandel and Neuenschwander57, Reference Liberati and D’Amico60).
Primary components of systematic reviews with meta-analysis
Given that traditional AD meta-analyses still dominate the literature, the emphasis of the rest of this manuscript will centre on this type of quantitative review but while noting that much of this information can be applied to many of the other types of systematic reviews with meta-analyses that have been previously described. For more detailed information, readers are referred to the PRISMA Guidelines, including a twenty-seven-item checklist, for the conduct and reporting of systematic reviews with AD meta-analysis(Reference Liberati, Altman and Tetzlaff30).
Overview
Similar to most research studies, a systematic review with meta-analysis manuscript (broadly) should consist of an abstract, introduction, methods, results, discussion and conclusion(s) section.
Abstract
The structure of the abstract of a systematic review with meta-analysis generally mirrors that of an original study. The PRISMA guidelines provide specific information, including a twelve-item checklist, regarding information to report in the abstract of a systematic review, with or without meta-analysis(Reference Beller, Glasziou and Altman61). However, adherence to all items in the checklist may be difficult given the word limitations on abstracts imposed by journals and conference abstracts. Thus, one may have to prioritise the most important information to be included, especially since many readers may not read beyond the abstract. For example, Saint et al. reported that almost two thirds (63 %) of internists only read the abstracts of medical journal articles(Reference Saint, Christakis and Saha62). Given the former, a clear and concise abstract would seem to be important.
Introduction
In the introduction section of the manuscript, the authors should provide a strong rationale for why the present study is needed. This should include the importance of the issue to be addressed as well as a review of prior research on the topic. Based on the authors’ experiences, producers of systematic reviews with meta-analysis usually provide an adequate description of the importance of the topic to be addressed but often lack information regarding previous original studies on the topic as well as previous systematic reviews with meta-analysis, if any, to justify their own systematic review with meta-analysis. The former is important because the conflicting findings of previous original studies are often one of the very reasons for conducting reviews of this nature. The latter is equally important because of the increasing concern about redundant systematic reviews, with or without meta-analysis, that is, value added(Reference Ioannidis9). If the authors are not aware of any previous systematic reviews with meta-analysis on the topic, then it should be stated. For example, in a systematic review with AD meta-analysis of randomised controlled trials examining the impact of modified dietary interventions on maternal glucose control and neonatal birth weight, Yamamoto et al. cited three previous systematic reviews and meta-analyses related to the topic but none specific to their proposed work regarding the impact of modified dietary interventions on detailed maternal glycaemic parameters, including changes in glucose-related variables(Reference Yamamoto, Kellett and Balsells63). As previously mentioned, one approach to help justify one’s own work, though more time-consuming and resource intensive, is to conduct and publish a systematic review of previous systematic reviews with meta-analysis on the topic and describe this in the introduction section of the manuscript(Reference Kelley and Kelley10). Finally, the end of the introduction should clearly delineate the purpose/objective(s)/research question(s) of the intended systematic review with AD meta-analysis.
Methods and results
Any systematic review, with or without meta-analysis, should include an a priori research plan and at a minimum, register the protocol in a systematic review trials registry such as PROSPERO(Reference Page, Shamseer and Tricco64). At the beginning of the methods section of the paper, the registration number should be reported. Registering a systematic review with meta-analysis is important for (1) promoting transparency, (2) helping to reduce potential bias and (3) helping to avoid unintended duplication of effort(Reference Stewart, Moher and Shekelle65). Registration is beneficial for researchers, commissioning and funding organisations, journal editors and peer reviewers(Reference Stewart, Moher and Shekelle65). Based on these benefits, the authors would advocate that journals require all manuscript submissions to include a registration number before being considered for peer review. In addition to the protocol being registered in PROSPERO, it is suggested that authors consider publishing their protocol in a peer-reviewed journal, thereby enhancing reach and possibly improving their study design. As an example, Asghari et al. recently published a protocol for a systematic review with AD meta-analysis in which they plan to examine the effects of vitamin D supplementation on serum 25-hydroxyvitamin D concentration in children and adolescents(Reference Asghari, Farhadnejad and Hosseinpanah66). The PRISMA group provides detailed guidelines, including a seventeen-item checklist, for developing and reporting the protocol for a systematic review, with or without meta-analysis (PRISMA-P)(Reference Shamseer, Moher and Clarke67). To enhance the field of research, the authors would also advocate that peer-reviewed journals consider publishing high-quality protocols, including requiring a completed PRISMA-P checklist upon submission.
Congruent with PRISMA guidelines,(Reference Liberati, Altman and Tetzlaff30) the methods section of a systematic review with AD meta-analysis should usually be partitioned into the following sections: (1) study eligibility, (2) data sources, (3) study selection, (4) data abstraction, (5) risk of bias assessment and (6) data synthesis.
Study eligibility. This section should describe the studies that should be included in a systematic review with AD meta-analysis. To aid in determining eligible studies as well as searching the literature, one may consider using the PICO or PICOS framework(Reference Liberati, Altman and Tetzlaff30). Where applicable, the PICO/PICOS structure includes participants/population (P), interventions (I), comparisons (C), outcomes (O) and study design/setting (S)(Reference Liberati, Altman and Tetzlaff30). For example, in a recent systematic review with AD meta-analysis on dietary patterns, bone mineral density and fracture risk, the PICOS framework included an open population (P), dietary patterns as the intervention (I), other dietary patterns as the comparison (C), bone mineral density, bone mineral content or fracture as the outcomes (O) and observational study designs (S)(Reference Denova-Gutierrez, Mendez-Sanchez and Munoz-Aguirre68). For observational studies dealing with aetiology, the population, exposure, control and outcomes framework has recently been suggested(Reference Dekkers, Vandenbroucke and Cevallos32). In addition, the type of study designs included should also be reported. For example, in a meta-analysis that examined the effects of Ca intake on breast cancer risk, the population consisted of females, the exposure was Ca intake (dietary and/or supplemental), the control/comparator was no dietary or supplemental Ca intake, the outcome was breast cancer risk and the study designs included were prospective cohort, case–control or case–cohort studies(Reference Hidayat, Chen and Zhang69).
In addition to providing a description of potential eligible studies, reasons for excluding studies may also be provided, though it is perfectly reasonable to assume that any study not meeting one’s eligibility criteria would be excluded. However, this does not exclude one from including a supplementary file of excluded citations, including the reasons for exclusion after each reference. A systematic review may include studies in any language, especially given the free online language translators that are currently available. However, there is no clear consensus regarding increased bias whether a systematic review is limited to English-language articles published in peer-reviewed journals(Reference Higgins and Green6). In addition, studies may be derived from both published and unpublished sources (master’s theses, dissertations, abstracts from conference proceedings, clinical trials registries, etc.). However, van Driel et al. concluded that (1) the difficulty in retrieving unpublished work could lead to selection bias, (2) many unpublished trials are eventually published, (3) the methodological quality of such studies are poorer than those that are published and (4) the effort and resources required to obtain unpublished work may not be warranted(Reference van Driel, De Sutter and De Maeseneer70).
Data sources. The data sources subsection of the methods describes the sources that are to be used to try and locate potential eligible studies. While there will always be a margin of search error, the goal is to try and obtain as many studies as possible that meets one’s eligibility criteria. To achieve this goal, a list of electronic databases that were searched should be provided (PubMed, Embase, etc.) as well as the search criteria for the databases. While there is no clear consensus, it has been suggested that at least two electronic databases be searched(Reference Higgins and Green6) because no one database indexes all journals. While a minimum of two databases is one suggestion(Reference Higgins and Green6), Bramer et al. recently suggested that at least Embase, MEDLINE, Web of Science and Google Scholar be searched to ensure adequate coverage(Reference Bramer, Rethlefsen and Kleijnen71). However, Google Scholar may not be worth the time and effort, given its lack of sensitivity and specificity(Reference Vine72). For those researchers who do not have easy access to Embase but can access Scopus, searching the latter may be acceptable since Scopus has been reported to provide 100 % coverage of both MEDLINE and Embase(Reference Burnham73). It is also relevant to point out that MEDLINE is nested within the PubMed database. If grey literature is included, sources such as ProQuest master’s theses and dissertations and the System for Information on Grey Literature in Europe databases could be searched. When searching electronic databases, the detailed search strategy for at least one of them, for example, PubMed, should be included. This may be embedded in the text or included as a supplementary file. To ensure adequate coverage, it is recommended that nutritionists search a minimum of three databases, inclusive of the following: (1) PubMed, (2) Embase or Scopus and (3) Web of Science.
In addition to searching electronic databases, other methods should be used. These include such things as cross referencing from retrieved studies, searching clinical trials databases, hand-searching selected journals and expert review. The start and end dates for all searches should be provided, including the reason(s) for the chosen start date. Finally, the name(s) of the individual(s) who conducted the searches should also be provided(Reference Liberati, Altman and Tetzlaff30).
Study selection. The study selection section describes the process that was used to select studies. To avoid study selection bias, studies should be reviewed by at least two people, independent of each other. Those individuals should then meet and review their selections for agreement. However, prior to doing so, one may provide data on the level of agreement before addressing discrepancies. One common statistic used to address this is the kappa statistic (κ)(Reference Cohen74). If agreement cannot be reached for one or more studies when the selectors meet, at least one other person should make a recommendation. For all excluded studies, the reason(s) for exclusion should be recorded. One broad way to address exclusions is to follow the PICOS structure: (1) participants/population, (2) intervention, (3) comparison, (4) outcomes, (5) study design/setting and (6) other. The names of all individuals involved in the study selection process, including their role, should also be provided.
Data abstraction. The data abstraction/extraction section describes the process used to code the eligible studies. A first step is to provide a brief description of how the codebooks were developed to abstract data, including a list and description of the information that was coded. Generally, this may include (1) study characteristics (authors, year of publication, journal, study design, etc.), (2) participant characteristics (age, gender, race/ethnicity, morbidities, etc.), (3) intervention characteristics (length of study, etc.) and (4) outcome characteristics (sample sizes, means, standard deviations, etc.). Additional information for abstracting data, including for complex meta-analyses, is provided elsewhere(Reference Pedder, Sarri and Keeney75). The same process for selecting studies should be used for abstracting data. In addition, the authors should provide information on the process used for obtaining missing data. If no attempt was made to obtain missing data, then this should be stated.
Risk of bias assessment. A systematic review, with or without meta-analysis, should usually include some type of risk of bias assessment for each included study. It is important here to distinguish between the risk of bias and study quality, something that appears to often be overlooked given the authors’ more than 25 years of experience in reviewing manuscripts and grant proposals. The Cochrane Collaboration recommends that the focus be on the risk of bias, amongst other factors, given that the ultimate goal should be the degree to which the results of the concluded studies are to be believed(Reference Higgins and Green6). It also overcomes the uncertainty in differentiating between the quality in the conduct of a study v. the conduct in the reporting of a study(Reference Higgins and Green6). While this does not negate the use of study quality scales, the potential limitations should be clearly delineated in the manuscript. However, the use of quality scales to decide what studies should be included or excluded is strongly discouraged, as previously mentioned, given the difficulty in distinguishing between the quality of the reporting of a study and the quality in the conduct of a study(Reference Higgins and Green6). There are at least eighty-six risk of bias/study quality assessment instruments(Reference Sanderson, Tatt and Higgins76). Seehra et al. reported that the Cochrane risk of bias was the most common tool used for assessing randomised controlled trials (26·1 %), while the Newcastle–Ottawa scale, a study-quality instrument, was used most commonly for assessing non-randomised studies (15·3 %), including case–control and cohort studies(Reference Seehra, Pandis and Koletsi77). However, since the time of this publication, the Cochrane Collaboration has updated their risk of bias tool for randomised controlled trials(Reference Higgins, Sterne and Savović78) and also created an instrument for assessing the risk of bias in non-randomised studies in which the health effects of two or more interventions are compared(Reference Sterne, Hernán and Reeves79). For authors, the important point here is to carefully consider the instrument(s) to be used and provide a rationale for the choice(s). For example, the authors may choose to use some type of risk of bias assessment instrument as well as some type of study quality tool. Finally, the processes for evaluating the risk of bias and/or the study quality are the same as those for selecting studies and extracting data. While not without limitations, the risk of bias and/or study quality results can help consumers of meta-analyses with decisions regarding the strengths and potential limitations of included studies.
Data synthesis (effect size calculation). The data synthesis piece of a systematic review can be either qualitative or quantitative (meta-analysis). The focus here will be on the meta-analytic approach. The initial step in conducting a meta-analysis is deciding on the method that will be used to calculate a common effect size for each outcome from each study so that the findings might be pooled into an overall result. The calculation of an effect size traditionally comprises sample sizes as well as measures of central tendency (e.g. means) and dispersion (e.g. standard deviations). If feasible, the focus should be on calculating and reporting effect sizes using the original metric, for example, kJ/d. The primary reason for this approach is based on the belief that it will be easier for consumers (nutritionists, clinicians, policymakers, etc.) to understand. However, in many situations, the calculation of something like a standardised mean difference effect size (Hedge’s g, Cohen’s d, etc.) may be necessary if the outcome of interest is assessed using different scales, for example, the effects of dietary improvement on symptoms of depression and anxiety, given that depression and anxiety outcomes were assessed using different scales(Reference Firth, Marx and Dash80). Another strength of the standardized mean difference effect size is the ability to calculate this statistic from a number of different tests (t tests, F ratios, correlations, etc.)(Reference Higgins and Green6, Reference Borenstein, Hedges and Higgins81). Alternatively, one potential weakness of the standardized mean difference effect size is the inability of consumers to understand this metric. For example, it is usually much easier for consumers to understand and interpret a decrease in resting systolic blood pressure of 8 mmHg v. a mean reduction of 0·50 standardised deviation units. Given the former, it is recommended that the original metric be used if all of the studies for the outcome of interest report the results for that outcome using the same metric or if the results can be converted into a metric that is easier for the reader to interpret, for example, converting total cholesterol (TC) from mg/dl to mmol/l by multiplying TC in mg/dl by 0·02586. If the outcome of interest is assessed using different instruments with various scales that cannot be converted into a more easily understood metric, then the standardised mean difference effect size is recommended. If the standardised mean difference effect size is used, we recommend that results based on the original scale, including variance statistics, also be reported in a table or figure.
Data synthesis (effect size pooling). After deciding on the metric used to pool results, a decision needs to be made on the type of model that will be used to pool results. However, prior to that decision, the investigators need to decide which study designs to include. For intervention studies, we recommend that only randomised controlled trials be included because they are the only way to control for confounders that are not known or measured as well as the observation that non-randomised controlled trials and single group trials tend to overestimate the effects of healthcare interventions(Reference Sacks, Chalmers and Smith82, Reference Schulz, Chalmers and Hayes83). For observational studies, we recommend that case–control, cross-sectional as well as retrospective and prospective study designs be analysed separately. These separate results can easily be displayed in a table and/or forest plot.
For pooling, there is currently no clear consensus on the one best model for combining results, necessitating a clear need for a large simulation study that tests all the different models under various conditions. With a focus on frequentist meta-analysis, historically two basic types of models are used, the traditional fixed-effect model and the random-effects model. In a traditional fixed-effect model, the assumption is that all the included studies share the same common effect size. Thus, any differences in the observed effects are considered to be the result of within-study sampling error while between-study variance is not accounted for. In contrast, random-effects models assume that the true effect size may differ both within (within-study sampling error) and between (between-study variance) studies. Thus, random-effects models attempt to account for both within- and between-study variance. Multiple random-effects models exist, all of which use different statistical approaches to estimate the between-study variance(Reference DerSimonian and Kacker84–Reference Sidik and Jonkman89). Therefore, if a random-effects model is used, it is important for authors to report and cite that random-effects model since they can lead to different results(Reference Zeng and Lin90). The most commonly used, but not necessarily the best model, is the original random-effects, method-of-moments approach of Dersimonian & Laird(Reference Dersimonian and Laird85). Its common use is most likely the consequence of its longevity as well as presence in numerous statistical packages for meta-analysis. The former notwithstanding, caution may be warranted in the a priori use of the traditional fixed-effect model and various random-effects models that are currently available(Reference DerSimonian and Kacker84–Reference Sidik and Jonkman89). For the traditional fixed-effect model, the issue has to do with not accounting for potential between-study variance that may exist. For random-effects models, an attempt is made to account for between-study variance that usually results in wider CI but also results in an increased mean squared error, which is a problem. In addition, the pooled mean effect for random-effects models is not always more conservative than the traditional fixed-effect model(Reference Poole and Greenland91). Alternatively, fixed-effect models with robust error estimation may currently be the best choice(Reference Doi, Barendregt and Khan92–Reference Doi, Furuya-Kanamori and Thalib94). In the presence of statistical homogeneity, these models will collapse into the traditional fixed-effect model. Both the inverse heterogeneity (IVhet) and quality effects (QE) models are examples of fixed-effect models with robust error estimation(Reference Doi, Barendregt and Khan92, Reference Doi, Barendregt and Khan93). Both have been shown to be more robust than the traditional Dersimonian and Laird approach, with regard to coverage probabilities(Reference Doi, Barendregt and Khan92, Reference Doi, Barendregt and Khan93). The IVhet model uses an estimator under the fixed-effect model assumption but importantly has a quasi-likelihood-based variance structure(Reference Doi, Barendregt and Khan92), while the QE model weights studies by including a quality score for each study, derived from a pre-existing or self-developed scale(Reference Doi, Barendregt and Khan93). The relationship between the two models is that the IVhet model is the QE model with quality set to equal. Thus, no quality scores need to be imputed when using the IVhet model(Reference Doi, Barendregt and Khan93).
While acknowledging the current and ever-changing state of the evidence as well as the prioritisation of coverage probabilities over point estimates, we recommend that the IVhet and QE models be used when conducting an AD meta-analysis(Reference Doi, Barendregt and Khan92–Reference Doi, Furuya-Kanamori and Thalib94). However, it’s also important to understand that no statistical model is perfect. In addition, the choice of which model to use will often depend on how a meta-analyst poses the question and what modelling assumptions they make a priori, including what the parameter of interest is. Both the IVhet and QE models are currently available in a free, easy-to-use Excel meta-analysis add-in program (Meta XL)(Reference Barendregt and Doi95). A Stata module (admetan) is also available to execute the IVhet and QE models.
Irrespective of model choice, and assuming a frequentist approach is used, pooled results should typically be reported using point estimates and 95 % CI as well as z- or t-based α values. While not germane to meta-analysis, one should consider when reporting and interpreting results the recent recommendations in an editorial by Wasserstein et al.(Reference Wasserstein, Schirm and Lazar3) as well as the rest of an entire issue of The American Statistician devoted to the use and over-reliance on ‘statistical significance’. Similiar recommendations were made in a recent commentary by Amrhein et al.(Reference Amrhein, Greenland and McShane96).
In addition to 95 % CI(Reference Amrhein, Greenland and McShane96), 95 % prediction intervals (PI) may also be reported when findings are pooled from those based on models such as random-effects(Reference Higgins, Thompson and Spiegelhalter97). The concept behind PI is that they tell one how effects are distributed around a summary effect(Reference Higgins, Thompson and Spiegelhalter97). This is in contrast to point estimates and CI, which provide an estimate of the overall effect and precision, respectively(Reference Higgins, Thompson and Spiegelhalter97). From an applied perspective, PI may make more sense because they help to determine uncertainty about whether an intervention works or not(Reference Higgins, Thompson and Spiegelhalter97). However, it has been recommended that caution be derived in drawing strong conclusions from 95 % PI because of coverage problems(Reference Partlett and Riley98). In addition, it has been suggested that because PI are calculated based on trials that are generally homogeneous, that is, patient populations and comparator treatments are interchangeable, the overall effect estimates may not be accurate if they do not meet this criterion(Reference Kriston99). As an example of PI use in nutrition, Cariolou et al. recently conducted an AD meta-analysis on the association between 25-hydroxyvitamin D deficiency and mortality in children with acute or critical conditions(Reference Cariolou, Cupp and Evangelou100). Based on a random-effects model, the pooled OR and 95 % CI of the risk of mortality in vitamin D deficient v. vitamin D non-deficient acute and critically ill children was 1·81 (95 % CI 1·24, 2·64). However, based on 95 % PI (0·71, 4·20), there was much less certainty, that is, wider intervals that also included 1, regarding this association(Reference Cariolou, Cupp and Evangelou100).
Similar to original studies, it is important to examine and report data on heterogeneity and inconsistency in meta-analysis. In meta-analysis, heterogeneity refers to any type of variability between studies and may be categorised broadly as clinical (patient characteristics, etc.), methodological (blinding, allocation concealment, etc.) and statistical (differences in outcome assessments, etc.)(Reference Higgins and Green6). The Cochran Q statistic is typically used to examine heterogeneity(Reference Cochran101), while the I 2 statistic, an extension of Q, is used to examine inconsistency(Reference Higgins, Thompson and Deeks102). The Q statistic is a measure of statistical significance and given power problems, is typically reported as significant if the alpha (α) value is < 0·10 as opposed to < 0·05(Reference Higgins, Thompson and Deeks102). I 2 is a relative measure that ranges from 0 to 100 %, with higher values representative of greater inconsistency(Reference Higgins, Thompson and Deeks102), while τ 2 is an absolute measure of between-study heterogeneity. However, like any statistic, Q, I,2 or τ 2 are not perfect with respect to explaining all the potential sources of heterogeneity(Reference Ioannidis, Patsopoulos and Evangelou103).
A standard graphical method of reporting results from each study as well as the overall pooled effect is through the use of a forest plot. An example of a forest plot using the IVhet model(Reference Doi, Barendregt and Khan92) is shown in Fig. 2(Reference Kelley, Kelley and Roberts104). While not common given the different ways in which data are reported, sample sizes as well as change outcome means and standard deviations from each intervention group may also be displayed in a forest plot. However, to reduce bias, including studies that only report data in exactly the same way is strongly discouraged if the overall treatment effect and variance from each study can be calculated from other reported statistics.
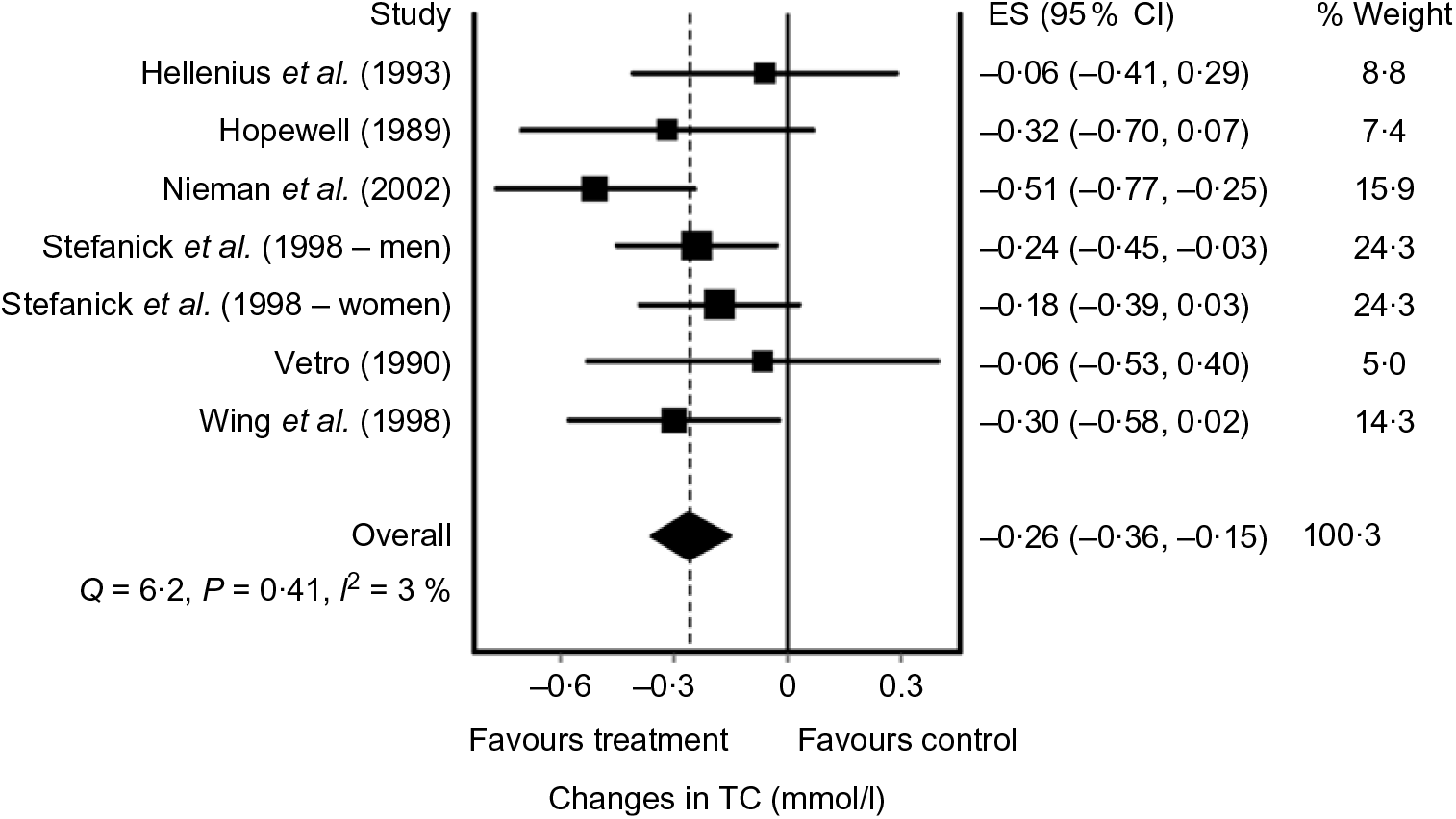
Fig. 2. Forest plot example of diet-induced changes in total cholesterol (TC) in adults based on the inverse variance heterogeneity (IVhet) model. The black squares represent mean changes in TC from each study while the left and right extremes of the squares represent the corresponding 95 % CI, that is, compatibility intervals for the mean changes. The middle of the black diamond represents the pooled mean change in TC, while the left and right extremes of the diamond represent the corresponding 95 % CI of the pooled mean change. The vertical dashed line represents the pooled mean change in TC while the solid vertical line represents zero (0) effect. As can be seen, the pooled 95 % CI did not include zero (0), suggesting compatibility regarding the association between diet and reductions in TC. The results for Cochran’s Q statistic, P value for Q and I 2 suggest a lack heterogeneity and inconsistency. The ES represents effect size changes in TC in mmol/l, while % weight represents the percentage weight attributed by each study to the overall pooled mean effect. Results were similar when the two results by Stefanick et al. were pooled into one overall ES. Data adapted from Kelley et al.(Reference Kelley, Kelley and Roberts104).
Data synthesis (small-study effects). An assessment for potential small-study effects (publication bias, etc.) is usually important in meta-analysis. Historically, this has most often been assessed qualitatively using some type of funnel plot and quantitatively using Egger’s test(Reference Egger, Davey Smith and Schneider105), though other methods exist for the assessment of both(Reference Sterne, Gavaghan and Egger106, Reference Furuya-Kanamori, Barendregt and Doi107). Briefly, a funnel plot is a scatterplot in which the precision of each included study (standard error, inverse of the standard error, etc.) is plotted on the vertical (y) axis and the effect size for each included study (mean difference, standardised mean difference, OR, etc.) is plotted on the horizontal (x) axis. In the absence of small-study effects, the values should appear as an inverted funnel, with smaller sample size studies showing greater dispersion, that is, larger standard errors, at the bottom of the plot, while studies with larger sample sizes showing less dispersion towards the top. Smaller missing studies without statistically significant effects will lead to an asymmetrical appearance of the funnel plot with a gap in the bottom corner of the plot. However, the funnel plot can be difficult to interpret(Reference Lau, Ioannidis and Terrin108). An example of a funnel plot using the same data as for the forest plot(Reference Kelley, Kelley and Roberts104) is shown in Fig. 3. Egger’s regression–intercept test is used for the Y intercept = 0 from a linear regression of a normalised effect estimate, that is, estimate divided by its standard error, against precision, that is, the reciprocal of the standard error of the estimate(Reference Egger, Davey Smith and Schneider105). Unfortunately, the power to detect asymmetry with Egger’s test is low when the number of studies is small(Reference Sterne, Sutton and Ioannidis109). Present recommendations suggest that if there are at least ten studies, a funnel plot and Egger’s test may be used to examine for the small-study effects if the outcome of interest is continuous in nature, for example, changes in TC. However, since the time of the publication of these recommendations, an alternative qualitative (Doi plot) and quantitative (Luis Furuya-Kanamori (LFK) index) approach have been suggested to be more robust with respect to ease in visualising asymmetry (Doi plot) as well as greater diagnostic accuracy in differentiating between asymmetry and no asymmetry (LFK index)(Reference Furuya-Kanamori, Barendregt and Doi107). Rather than use a scatterplot, the Doi plot uses a normal quantile plot v. effect rather than precision v. effect, providing better visualisation than a dot plot(Reference Furuya-Kanamori, Barendregt and Doi107). The LFK index, an index based on the Doi plot, assesses asymmetry quantitatively, with a value of zero (0) representing perfect symmetry, and thus, no apparent small-study effects(Reference Furuya-Kanamori, Barendregt and Doi107). It is based on the concept in which symmetry would be considered with respect to a vertical line on the horizontal (x) axis from the effect size with the lowest absolute z score on the Doi plot, dividing the plot into two regions with the same areas. The LFK index then quantifies the difference between these two regions in terms of the areas below the plot and the difference in the number of studies included in each arm of the plot(Reference Furuya-Kanamori, Barendregt and Doi107). Values ± 1, greater than ± 1 and within ± 2 and greater than ± 2 are considered to represent no, minor and major asymmetry, respectively(Reference Furuya-Kanamori, Barendregt and Doi107). An example of the Doi plot and LFK index using the same data as for our previous examples is shown in Fig. 4.
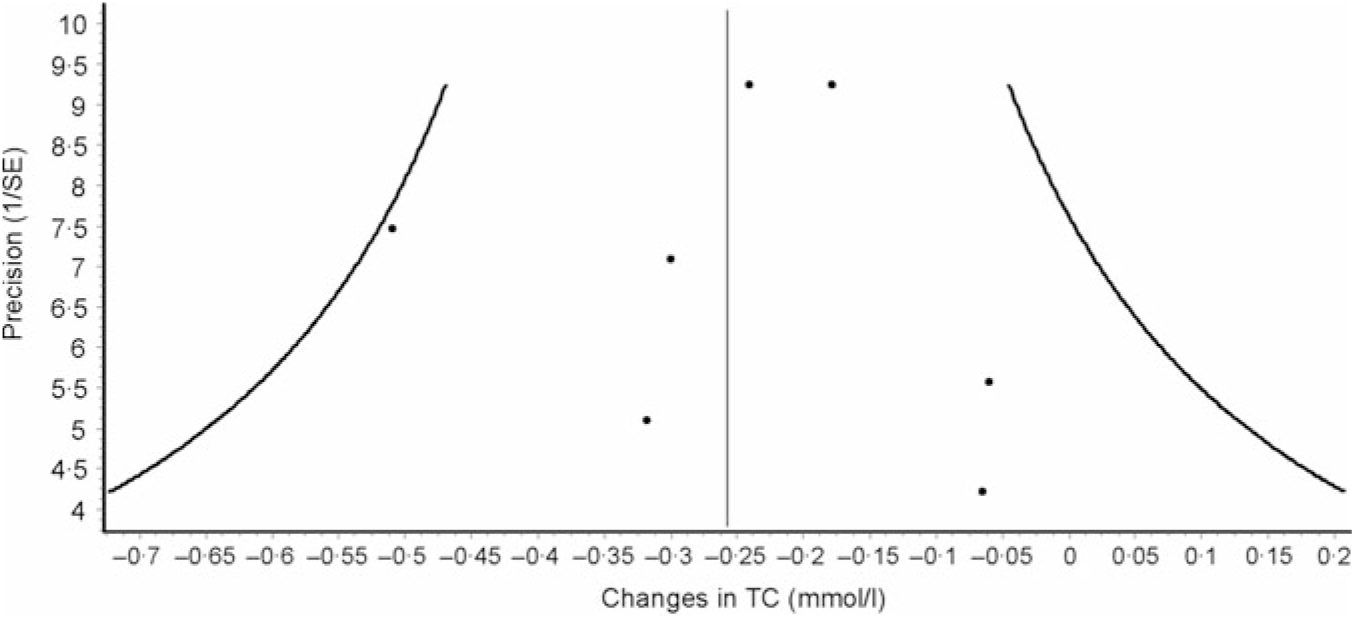
Fig. 3. Example of funnel plot based on diet-induced changes in total cholesterol (TC) following a dietary intervention. The solid vertical line represents the overall pooled mean change in TC in mmol/l after a dietary intervention. The x-axis represents changes in TC in mmol/l from each study while the y-axis represents the inverse of the standard error for changes in TC from each study. Each dot represents changes in TC plotted against its precision. In the absence of small-study effects, the plot should resemble a pyramid or inverted funnel, with scatter due to sampling variation. In the presence of potential small-study effects, the results from smaller studies with smaller/null findings will be missing in that region of the plot. While difficult to interpret, especially given the small number of effect estimates, there do not appear to be any small-study effects. Results were similar when the two results by Stefanick et al. were pooled into one overall effect size. Data adapted from Kelley et al.(Reference Kelley, Kelley and Roberts104).
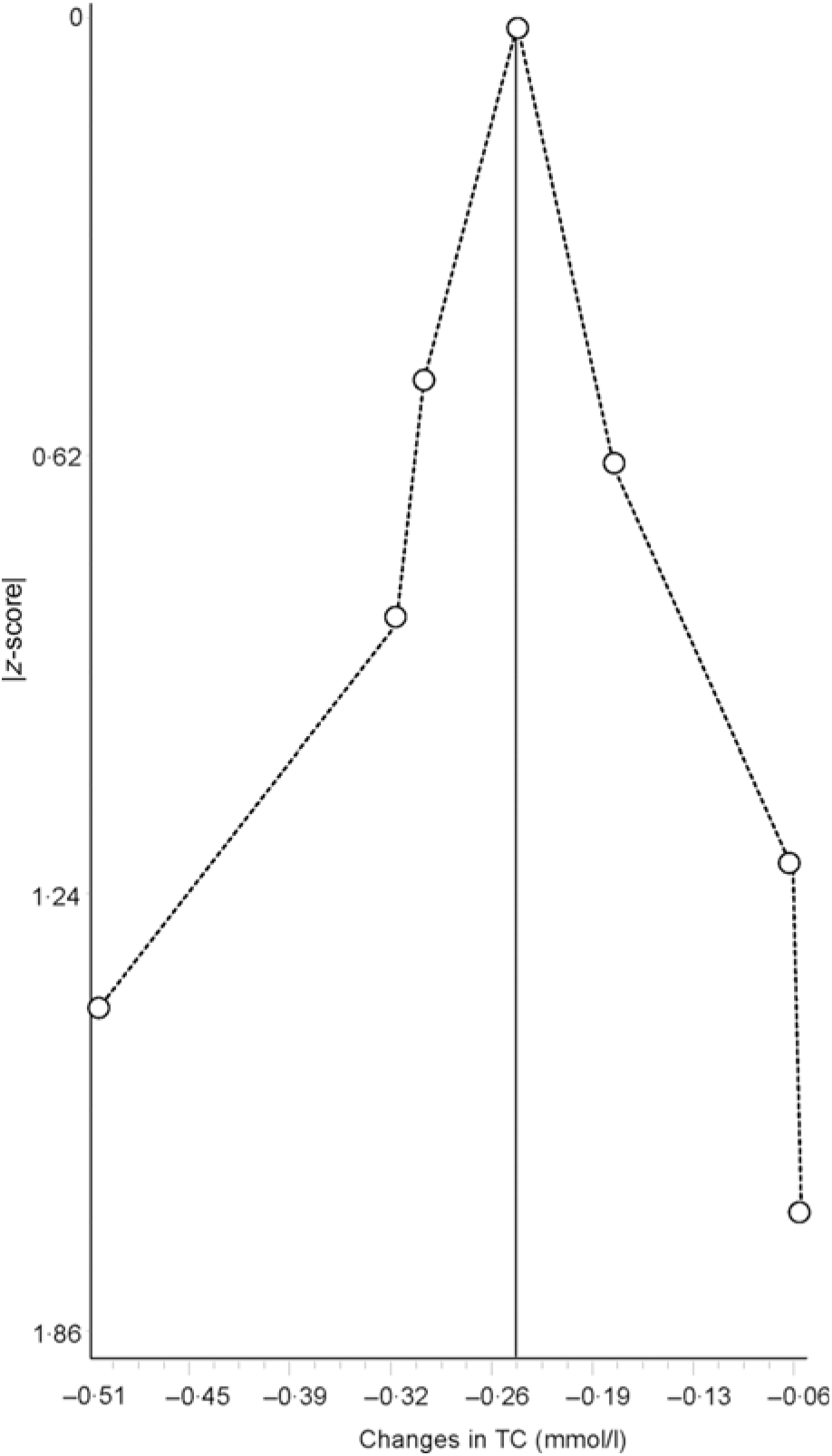
Fig. 4. Example of Doi plot based on diet-induced changes in total cholesterol (TC) following a dietary intervention. The vertical line on the horizontal (x) axis represents the effect size (ES) with the lowest absolute z score, dividing the plot into two regions with the same areas. Visualisation of the plot suggests no asymmetry and thus no small-study effects such as publication bias. The obtained Luis Furuya-Kanamori index of 0·30 also suggests no asymmetry. Results were similar when the two results by Stefanick et al. were pooled into one overall ES. Data adapted from Kelley et al.(Reference Kelley, Kelley and Roberts104).
Data synthesis (influence and cumulative meta-analysis). Many meta-analyses include a small number of trials. For example, it has been reported that the typical number of studies included in a Cochrane systematic review is six(Reference Mallett and Clarke110). Given the former, it is usually relevant to conduct influence analysis with each study deleted from the model once in order to examine the effect that each study has on the overall results. Fig. 5 provides an example of influence analysis using the same data as for our other examples(Reference Kelley, Kelley and Roberts104).
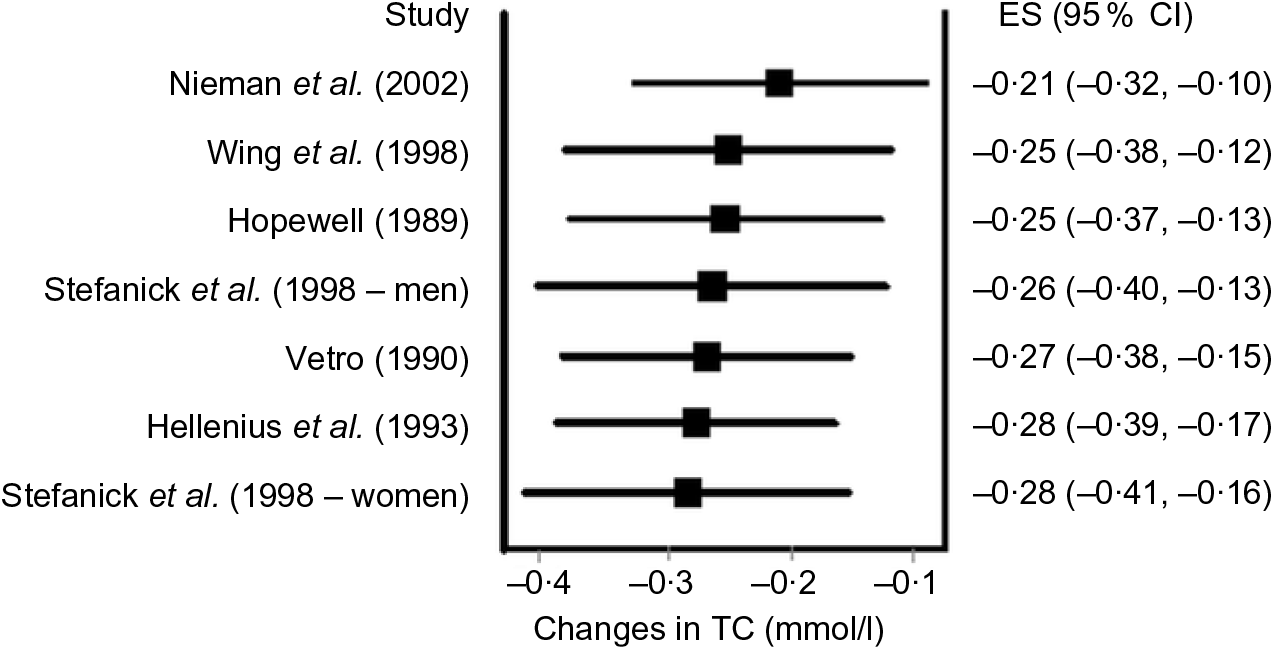
Fig. 5. Influence analysis based on the inverse variance heterogeneity model with each result deleted from the overall analysis once. The black squares represent mean changes in total cholesterol (TC) with the corresponding study deleted from the model, while the left and right extremes of the squares represent the corresponding 95 % CI for the mean changes. As can be seen, changes ranged from –0·21 to –0·28 mmol/l with non-overlapping 95 % CI for all. These findings suggest that no one result had a significant impact on the overall findings. Results were similar when the two results by Stefanick et al. were pooled into one overall effect size (ES). Data adapted from Kelley et al.(Reference Kelley, Kelley and Roberts104).
In addition to influence analysis, it is often relevant to conduct cumulative meta-analysis, traditionally ranked by year of publication, to examine the accumulation of results over time(Reference Clarke, Brice and Chalmers111). The inclusion of findings from a cumulative meta-analysis can aid in making more educated choices based on past years of research as well as leading to more timely and increased use of successful interventions in practice(Reference Clarke, Brice and Chalmers111). Using this method, findings are pooled as each additional study is added to the model. An example of cumulative meta-analysis using the same data as for our previous examples is shown in Fig. 6.
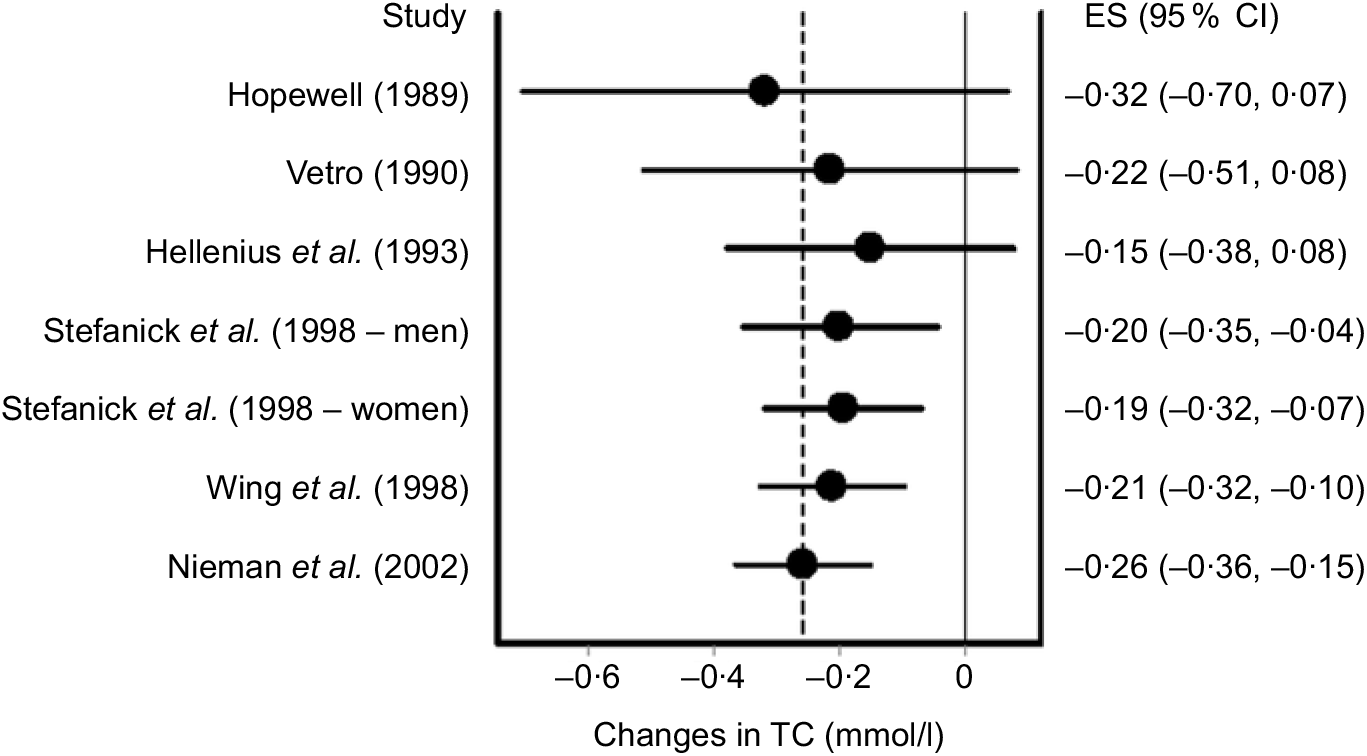
Fig. 6. Cumulative meta-analysis ranked by year and based on the inverse variance heterogeneity model. The black circles represent mean changes in total cholesterol (TC) with the corresponding study, and all earlier studies pooled while the left and right extremes of the circles represent the corresponding 95 % CI for the mean pooled changes. As can be seen, non-overlapping 95 % CI have been observed since 1998. Results were similar when the two results by Stefanick et al. were pooled into one overall effect size (ES). Data adapted from Kelley et al.(Reference Kelley, Kelley and Roberts104).
Data synthesis (subgroup and/or meta-regression analysis). Given an adequate number of studies, subgroup and/or meta-regression may be conducted to explore the effect of selected covariates, for example, age, on the outcome(s) of interest, for example, changes in fat mass as a result of a weight-loss intervention. Traditionally, these are based on weights derived from fixed and random-effects models, and more recently, approaches such as the IVhet and QE models, details for all of which have been described elsewhere(Reference Higgins and Green6, Reference Borenstein, Hedges and Higgins81, Reference Doi, Barendregt and Khan92, Reference Doi, Barendregt and Khan93, Reference Xu and Doi112, Reference Lopez-Lopez, Van den Noortgate and Tanner-Smith113). While there may be a propensity for investigators to only conduct analyses when statistically significant and/or a large amount of inconsistency is found, this is generally not advised, given the current limitations of measures for heterogeneity and inconsistency(Reference Higgins, Thompson and Deeks114). With respect to the number of studies needed to conduct analyses such as meta-regression, currently no firm consensus exists regarding this. However, as a broad recommendation, and while understanding the potential arbitrariness of any definitive number given the numerous factors to consider, we support the recommendation of Fu et al., in which there should be at least six studies per covariate for a continuous variable, for example, age, and at least four studies per group for a categorical variable, for example, sex (female, male)(Reference Fu, Gartlehner and Grant115). Exclusive of dose–response analyses, the four studies per group for a categorical variable is also recommended for any subgroup analyses conducted. If multiple meta-regression analysis is conducted, one should also consider conducting and reporting results for all simple meta-regression analyses performed. This may be especially relevant, given that such analyses in meta-analysis are considered to be exploratory. As a result, such findings would need to be tested in original studies because studies are not randomly allocated to covariates in meta-analysis. Consequently, they are regarded as observational. For categorical variables such as sex, there may be a lack of studies in one or more categories to conduct any type of meta-regression or subgroup comparisons. If this is the case, there are more than two categories, and it is scientifically plausible, one may collapse one or more categories, so that at least two exist. One can then conduct their meta-regression and/or subgroup analyses. If this is not possible, one may then consider additional forms of sensitivity analyses by omitting the results from the category with the smaller number of studies to see how it effects one’s overall results. As an example, if there are results from ten studies, eight in males and two in females, one may choose to run their analyses with only the results from the males to see how it compares with the overall pooled results.
One aspect of meta-analysis in nutrition as well as other fields is that some studies conduct and report on highest v. lowest tertile comparisons. However, these are almost always difficult to interpret in terms of what nutritionists should recommend, given that there is overlap between studies with respect to what is considered high and low. Indeed, some low categories could be minimal and well below current recommended daily allowances while others could be considered close to pharmacological. Since nutritionists tend to prefer a recommended intake that can be applied to various populations and groups with confidence, it is recommended that any such comparisons be conducted using a dose–response approach. This consists of modelling the association between the exposure and outcome to estimate the increase or decrease associated with one unit, or some other appropriate unit change, in exposure(Reference Dekkers, Vandenbroucke and Cevallos32). For example, using linear dose–response meta-analysis, Morze et al. found no significant associations between a 10-g/d increase in chocolate intake and heart failure (relative risk = 0·99, 95 % CI 0·94, 1·04) as well as type 2 diabetes (relative risk = 0·94, 95 % CI 0·88, 1·01)(Reference Morze, Schwedhelm and Bencic116). However, a small inverse association was observed for CHD (relative risk = 0·96, 95 % CI 0·93, 0·99), and stroke (relative risk = 0·90, 95 % CI 0·82, 0·98)(Reference Morze, Schwedhelm and Bencic116). Greenland & Longnecker(Reference Greenland and Longnecker117), Hartemink et al.(Reference Hartemink, Boshuizen and Nagelkerke118) and Xu et al.(Reference Xu and Doi112) provide detailed information regarding dose–response methods for meta-analysis.
Data synthesis (practically relevant information). An aspect that is sometimes overlooked when conducting a meta-analysis is the need to provide practically relevant information to readers. In addition to reporting both absolute and relative results whenever possible, the use of metrics such as the number needed to treat (NNT)(Reference Higgins and Green6, Reference da Costa, Rutjes and Johnston119) and percentile improvement based on values such as Cohen’s U 3 index(Reference Cohen120), when appropriate, could be considered. For example, using the diet and TC data from our previous examples(Reference Kelley, Kelley and Roberts104), the method of Hasselblad and Hedges for estimating the NNT from continuous data(Reference Hasselblad and Hedges121), and a control group risk of 30 %, the NNT for diet-associated reductions in TC was 5, meaning that one in five (20 %) people would reduce their TC if they dieted. Using the same data, Cohen’s U 3 index for percentile improvement was 16·9, meaning an improvement from the 50th to 66·9th percentile. In addition, one should also consider both the clinical and population health importance of any findings from a meta-analysis. For example, a 2-mmHg reduction in resting systolic blood pressure as a result of lower sodium intake may not be very important at the patient level but may have significant implications at the population level, given that lower sodium intake has been associated with a 4 % reduction in CHD and a 6 % reduction in stroke(Reference Stamler, Rose and Stamler122).
Data synthesis (strength of evidence). An assessment for the strength of the evidence for the outcome(s) of interest should usually be conducted and reported. One of the most common instruments used is the GRADE instrument, details of which are provided elsewhere(Reference Guyatt, Oxman and Vist123). In brief, GRADE is a subjective tool that assesses the strength of evidence for a specific outcome across five areas: (1) risk of bias, (2) imprecision, (3) inconsistency, (4) indirectness and (5) publication bias(Reference Guyatt, Oxman and Vist123). For each of these items, the evidence can be rated down by one to two levels. There can also be an increase of one or two levels if there is a large effect and/or an increase of one level if either a dose–response relationship is observed or all plausible confounding would reduce the effect or increase the effect if no effect was identified(Reference Guyatt, Oxman and Vist123). For the GRADE instrument, risk of bias focuses on study limitations that include lack of allocation concealment and blinding, incomplete accounting of participants and outcome events, selective outcome reporting as well as any other limitations that reviewers believe may impact the outcome(Reference Guyatt, Oxman and Vist123). Imprecision is the degree of uncertainty about the findings and includes such things as a wide CI around the estimate of effect, while inconsistency signifies unexplained heterogeneity in results(Reference Guyatt, Oxman and Vist123). Indirectness is the evaluation of findings based on whether the included studies directly compare the interventions and populations in which one is interested in as well as measuring outcomes believed to be important by participants, for example, self-reported health-related quality of life as a result of weight loss in obese participants. Lastly, publication bias is the selective publication of studies in which improvements are embellished and harms are underestimated(Reference Guyatt, Oxman and Vist123). The overall certainty of the evidence is then rated by the authors as either (1) very low, (2) low, (3) moderate or (4) high(Reference Guyatt, Oxman and Vist123). As an example of the use of the GRADE instrument in nutrition, Baranski et al. rated the overall strength of evidence as moderate or high for the majority of parameters for which significant differences were detected in a systematic review with meta-analysis on differences in composition between organic and non-organic crops and crop-based foods(Reference Baranski, Srednicka-Tober and Volakakis124).
Discussion and conclusions
Where appropriate, the discussion and conclusions sections of a systematic review with meta-analysis should include (1) a summary of the overall findings, (2) a discussion of how the findings compare with previous research on the topic, (3) the potential clinical, public health and policy implications of the findings, (4) directions for future research with respect to both the reporting of future studies on the topic and additional studies that might be needed, for example, the dose–response effects of vitamin D on bone mineral density and (5) the strengths and potential limitations of one’s systematic review with meta-analysis. With respect to the latter, one of the inherent limitations of any AD systematic review with meta-analysis is the potential for ecological fallacy(Reference Rucker and Schumacher125). The PRISMA guidelines provide greater details regarding items to include in the discussion and conclusion sections of a systematic review with meta-analysis(Reference Liberati, Altman and Tetzlaff30).
With respect to interpretation on the part of the consumer, the results of a systematic review with meta-analysis should be considered, broadly, with respect to several potential factors. First and foremost, were any significant findings also found practically important? Second, were the included studies representative of the population, exposures and outcomes that one is interested in and deemed to be important? Third, do any potential benefits outweigh the risks involved? Fourth, is the evidence considered to be strong?
Finally, meta-analysis, like many fields today, is progressing at a rapid pace. As a result, it is very difficult for generic statisticians, biostatisticians and other relevant professionals to stay current unless they have a specific and current focus in this burgeoning field. Given the former, we strongly recommend that not only a content expert but also a meta-analytic expert be included in any meta-analysis that is conducted.
Conclusion
The number of systematic reviews, with or without meta-analysis, is increasing in the field of nutrition. The purpose of this article was to provide a non-technical introduction to producers, reviewers and consumers of these important reviews, with a focus on nutrition. It is the hope that this information will be helpful to producers, reviewers, and consumers in the field of nutrition.
Acknowledgements
No funding was received for this work.
G. A. K. was responsible for the conception and design, acquisition of data, analysis and interpretation of data, drafting the initial manuscript and revising it critically for important intellectual content. K. S. K. was responsible for the conception and design, acquisition of data, drafting the initial manuscript and revising all drafts critically for important intellectual content. Both authors read and approved the final manuscript.
There are no conflicts of interest.
Patient consent
Not required.
Data sharing statement
All data are available upon request from the corresponding author.









