Low vitamin D status is linked to rickets and osteomalacia, with some evidence to suggest that it may also be implicated in a range of diseases including osteoporosis, some types of cancer, CVD, tuberculosis, multiple sclerosis and type 1 diabetes(Reference Holick1). Quite what should be the relative contributions of oral vitamin D intake and sunlight exposure to maintain and achieve an adequate vitamin D status, especially during the winter in ‘at-risk’ population groups, is not clear(Reference Ashwell, Stone and Stolte2).
The usual measure of vitamin D status is the circulating level of 25-hydroxyvitamin D (25(OH)D), which incorporates both vitamins D2 and D3 from oral intake (principally diet) and vitamin D3 from sun exposure. In the present study, a mathematical model is developed for estimating changes in plasma 25(OH)D levels throughout the year resulting from the oral intake of vitamin D and the behaviour outdoors of white British adults resident in different regions of the UK.
The outputs from the model developed here can be used to inform the Scientific Advisory Committee on Nutrition's risk assessment on vitamin D and health and may contribute towards updating dietary reference values for the British population.
Methods
The model is a development of one described previously(Reference Diffey3) and extended by Krzyścin et al. (Reference Krzyścin, Jarosławski and Sobolewski4). The principal differences between the existing model and previous ones(Reference Diffey3, Reference Krzyścin, Jarosławski and Sobolewski4) are that it accounts for variable oral intake, and the uptake and release of vitamin D from tissue stores, and uses data from recent experimental studies to inform the biokinetic parameters.
The total plasma 25(OH)D concentration in nmol/l on day T, C total(T), comprises contributions from both oral and solar sources, and is the sum of the concentration on the previous day, C total(T− 1), and the change in 25(OH)D between day T and T− 1, due to oral intake and sun exposure. This is expressed mathematically as:
The plasma 25(OH)D concentration due to the diet and/or supplements on day T, C oral(T), is the consequence of oral intake O(t) on all previous days t weighted according to a response function (R oral(t)) that represents the plasma 25(OH)D concentration t days after a single oral dose. This can be expressed as:
The plasma 25(OH)D concentration due to sunlight on day T, C sun(T), is the consequence of sun exposure E(t) on all previous days t weighted according to the area of exposed skin (A(t)) on day t, and a response function (R UV(t)) that represents the plasma 25(OH)D concentration t days after a single solar UV exposure, and is expressed as:
The factor F(T) accounts for the observation that changes in plasma 25(OH)D concentration induced by a given UV exposure are more effective for subjects having lower initial 25(OH)D concentrations. Bogh et al. (Reference Bogh, Schmedes and Philipsen5) exposed 24 % of the body surface area (BSA) of fifty subjects with a wide range in baseline 25(OH)D levels to a fixed dose of UVB. They found that the increase in 25(OH)D levels after UVB exposure was negatively correlated with baseline 25(OH)D levels, and regression analysis applied to their data gave the following expression:
The boundary condition is that C oral(0), C sun(0) and hence C total(0) are equal to zero. Since plasma 25(OH)D levels following a single UV exposure and/or a single oral dose fall slowly, results are always shown for year 4 by which time the relative year-to-year change is less than 1·5 %.
The model, which does not differentiate between sex, is constructed within an Excel spreadsheet using standard Excel functions. Tabular and graphical display of the daily variation of plasma 25(OH)D throughout the year is immediate following the user's choice of input variables, such as time and behaviour outdoors and/or oral intake. The spreadsheet is available from the author on request.
Personal sun exposure
Our sun exposure is both adventitious, such as casual exposure during the working week, and elective during our recreational exposure at weekends and on holiday. The daily personal sun exposure on weekdays (E wd) for a specific geographical location and month is determined using a simple behavioural model(Reference Diffey6) such that the UV exposure to sun-exposed vertical body sites, such as the face, is calculated as:
where < UV> is the mean daily ambient erythemal UV in standard erythema doses (SED) (the SED(7) is a measure of erythemally effective UV; it requires an exposure of about 2–5 SED of sun exposure to result in the minimal reddening of unacclimatised white skin 8–24 h later) averaged over the month; EFwd is the exposure fraction, i.e. the fraction of ambient UV received on normally exposed sites and is a consequence of posture and the surrounding environment; h wd are the hours per d spent outside on weekdays; H is the hours of daylight averaged over each day during the month, calculated using an established astronomical equation(Reference Diffey6). In order to maintain a simple approach to modelling, it is assumed that the hours spent outside h wd are symmetrical about the solar noon and that the irradiance of solar erythemal UV exhibits a triangular distribution between the sunrise and the sunset, peaking at solar noon, the latter assumption being well supported from the diurnal variation of erythemal UV at different latitudes(Reference Diffey6).
Personal sun exposure on weekend days is expressed similarly:
where EFwe is the exposure fraction received on weekends, and h we are the hours per d spent outside during weekends.
For indoor workers, whose time spent outdoors during weekdays is generally in an urban environment, exposed sites such as the face and hands typically receive about 0·15 of the ambient UV that is incident on an unshaded, horizontal surface(Reference Diffey6) due to the combined effect of body geometry, random orientation with respect to the sun, partial obstruction of the sky, and possibly direct shading of sunlight by nearby buildings.
At weekends, especially during recreational exposure, more time may be spent away from urban areas where a much greater part of the sky will be visible and the shade of direct sunlight less frequent. Consequently, the weekend exposure fraction EFwe was increased to 0·25.
It is evident that there is an appreciable variation in the time spent outdoors during a specific exposure period (e.g. summer weekends) by habitués. The results of a meta-analysis on time spent outdoors during the summer season(Reference Diffey8) indicated that weekday and weekend exposures are positively skewed with median times per d spent outdoors close to 1 and 1·5 h, respectively.
The personal sun exposure calculated here does not take into account protective behaviours such as sunscreen use or wearing a hat that result in shadow over the face; such behaviour would modify the UV dose absorbed in the skin, and hence the vitamin D synthesis.
Exposed skin
During the winter, it is generally just the hands, face and neck that are exposed, equivalent to about 6–10 % of the BSA(Reference Lund and Browder9). In the summer, there will be a tendency for some people to expose their arms during the working week, which together with the face, neck and hands comprises about 15–20 % of the BSA. Also, during summer weekends and holidays, the lower legs will often be exposed resulting in about 30 % of the BSA.
For typical personal daily doses (generally < 1 SED) and exposed body surfaces (generally < 20 %) encountered in day-to-day life, which is the nature of exposure reflected by the model, the increase in 25(OH)D has been shown to be proportional to the product of UV exposure and the fraction of exposed BSA(Reference Bogh, Schmedes and Philipsen10); although for significant (>40 %) exposed BSA and UV exposures encountered during extended periods of recreational exposure in the sun such as occurs on vacation and where erythema is often a consequence, the assumption that vitamin D synthesis increases in proportion to the product of dose and area is invalid(Reference Bogh, Schmedes and Philipsen10).
The UV response function RUV(t)
The UV response function (R UV(t)) represents the plasma 25(OH)D concentration t days after a single UV exposure, and is described here by a two-compartment model that accounts for the plasma uptake, plasma clearance and uptake and clearance by tissue stores of 25(OH)D, by the following expression:
where A is a scaling factor such that R UV(t) represents plasma 25(OH)D concentration per SED for 1 % of BSA exposed; f is the fraction of synthesised vitamin D stored in tissue; α, β and γ are the half-times for plasma uptake, plasma clearance and tissue store clearance, respectively.
Following a single whole-body exposure of eleven healthy volunteers on a commercial sunbed (UVB comprised 2 % of the total UV emission), blood samples were analysed for 25(OH)D at baseline, 15 min, 1, 2, 4, 6 h, 1, 2, 3 and 7 d post-exposure(Reference Langdahl, Schierbeck and Bang11). The resulting time course showed a rapid rise followed by a steady state between 2 and 7 d and by non-linear regression analysis on these data, the half-time for uptake (α) was estimated as 0·6 d.
The half-life (β) for plasma clearance of 25(OH)D has been reported as 2 weeks(Reference Holick12) and 3–4 weeks(Reference Clements, Davies and Hayes13). A more recent estimate(Reference Lips14) reported that the half-life of plasma 25(OH)D is about 25 d, and so we adopt this value for β.
The dynamics of vitamin D storage in body tissues and re-entry into the circulation remain poorly understood, although it has been suggested that tissue storage can last for months or even years(Reference Macdonald, Mavroeidi and Fraser15). Consequently, a two-compartment model for the time course of plasma 25(OH)D is used. To obtain estimates for the fraction (f) of synthesised vitamin D stored in tissue and for the half-time (γ) for tissue store clearance, data on groups who have been deprived of UV radiation for several months were used. The subsequent analysis (see below) resulted in estimates of 0·15 for the fraction (f) and a half-time (γ) for tissue store clearance of 250 d.
Finally, data from an intervention study were used to estimate the scaling factor A. This study(Reference Rhodes, Webb and Fraser16), carried out over the winter, involved 120 white Caucasians aged 20–60 years who received a sun equivalent dose of 1·1 SED three times per week for 6 weeks while wearing T-shirt and shorts, resulting in about 30 % of BSA irradiated. Plasma 25(OH)D was measured at baseline and again at weekly intervals until the end of the study. The model was run using the appropriate inputs (1·1 SED three times per week and 30 % BSA) and the scaling factor optimised to obtain the best fit, which resulted in a value of A of 0·18 nmol/l per SED per cent of BSA.
So using data from a number of independent experimental studies, we obtain values of the biokinetic parameters A, f, α, β and γ; the response function, R UV(t), calculated using these values is shown in Fig. 1.

Fig. 1 Time-varying concentration of plasma 25-hydroxyvitamin D (25(OH)D) in response to a single solar UV exposure of 1 standard erythema dose (SED) UV to 1 % of the body surface area calculated according to equation 7.
The oral intake response function Roral(t)
The time course of 25(OH)D was measured over a 4-month period in a group of thirty healthy, community-dwelling, predominantly white men and women (age range 27–84 years) following a single oral dose of 2500 μg of cholecalciferol(Reference Ilahi, Armas and Heaney17). The results from this study are shown by the data points in Fig. 2 and the solid line is given by the expression:
where R oral(t) is a response function that represents plasma 25(OH)D concentration per μg intake. We assume that the kinetics of plasma and tissue clearance of 25(OH)D are the same irrespective of whether the source is oral or UV, and so we take R oral(t) to have the same form as was used above for the UV response function R UV(t):

Fig. 2 Time-varying concentration ( ± 1 sem) of plasma 25-hydroxyvitamin D (25(OH)D) following a single oral dose of 2500 μg cholecalciferol (modified from Ilahi et al. (Reference Ilahi, Armas and Heaney17)). Response expressed by equation 8 (![]() ).
).
where S is a scaling factor and α′ is the half-time for uptake from oral intake, which is not necessarily the same as for UV synthesis. We take the remaining terms f, β and γ to be numerically identical to those derived for the UV response function. Using the Solver capability of Excel, S and α′ were determined to be 0·018 nmol/l per μg and 1·5 d, respectively. It may be seen from Fig. 2 that the modelled function given by equation 9 is commensurate with the uncertainties associated with the experimental data.
The steady-state cholecalciferol input required to achieve an equilibrium plasma 25(OH)D concentration is determined as:
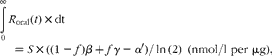 $${ \int _{0}^{\infty } }\, R _{oral}( t )\times dt = S \times ((1 - f ) \beta + f\gamma - \alpha \prime )/\,ln\,(2)\ (nmol/l\,\,per\,\,\mu g), $$
$${ \int _{0}^{\infty } }\, R _{oral}( t )\times dt = S \times ((1 - f ) \beta + f\gamma - \alpha \prime )/\,ln\,(2)\ (nmol/l\,\,per\,\,\mu g), $$which equals 1·52 nmol/l per μg. Other authors have estimated equilibrium values (in nmol/l per μg) of 0·56(Reference Vieth, Chan and MacFarlane18) 0·70(Reference Heaney, Davies and Chen19) and 1·15(Reference Vieth, Chan and MacFarlane18), with six studies(Reference Byrne, Freaney and McKenna20–Reference Cashman, Hill and Lucey25) yielding values in the range 1·6–2·2. The median value of these nine estimates is 1·9 nmol/l per μg, resulting in a revised value of S of 0·023 nmol/l per μg; this exemplary value will be used henceforth in equation 9.
Results
Modelled seasonal variation of 25-hydroxyvitamin D in a British population
The habitual mean daily dietary vitamin D in British people is generally in the range 2–4 μg(Reference Henderson, Irving and Gregory26), and calculations were carried out using an exemplary oral vitamin D intake (O(t); equation 2) of 3 μg/d. Time spent outdoors, exposure fraction (reflecting urban or non-urban environment) and area of exposed skin at different times of the year that could be regarded as representative of the typical behaviour of British indoor workers are summarised in Table 1.
Table 1 Variables that are assumed to reflect representative behaviour of British people outdoors

All results presented here assume a British population and ambient UV data were available in approximately 2° latitude steps from southern England (latitude 50°N) to the Shetland Islands (latitude 60°N). Monthly values of mean daily ambient UV for each region were averaged over the 16-year period (1995–2011) and used as estimates for < UV> (Table 2).
Table 2 Average daily ambient solar UV radiation (in standard erythema doses; SED) measured at different locations in Great Britain (courtesy of the Health Protection Agency)

We assume that weekday exposure for much of the year is limited to the hands, face and neck (10 % BSA) except for the months of June, July, August and September where the BSA is increased to 15 %, reflecting that many people will be exposing forearms in addition. For weekend exposure from June through to September, the BSA is taken as 15–20 % to reflect the opportunity taken by some people to expose arms and legs in addition to normally exposed sites. The resulting variation of plasma 25(OH)D throughout the year is shown by the solid line in Fig. 3, calculated assuming ambient UV typical of the English Midlands, which is the region corresponding to the centre of population of Great Britain.

Fig. 3 Modelled annual variations in 25-hydroxyvitamin D (25(OH)D) for an oral vitamin D intake of 3 μg/d, and times per d spent outdoors during weekdays and weekends of 30 and 45 min (lower broken curve), 1 and 1·5 h (solid curve) and 2 and 3 h (upper broken curve). Data are geometric mean monthly 25(OH)D concentrations with 95 % CI represented by vertical bars measured by Hyppönen & Power(Reference Hyppönen and Power27).
The impact of sun-avoidance behaviour, which we take to be times spent outdoors per d of 30 and 45 min for weekdays and weekends, respectively, is illustrated by the lower dashed line in Fig. 3. Similarly, sun-seeking behaviour, which we take to be 2 and 3 h spent outdoors per d for weekdays and weekends, respectively, is illustrated by the upper dashed line in Fig. 3.
Also shown in Fig. 3 are the geometric mean monthly plasma 25(OH)D concentrations measured by Hyppönen & Power(Reference Hyppönen and Power27). These authors measured plasma 25(OH)D in over 7000 white British people from the 1958 birth cohort when they were 45 years of age during the period September 2002 to April 2004. The modelled and measured data both show a minimum in late February/early March and a peak in late August/early September with a close agreement between the measured data and that calculated for ‘typical’ behaviour.
It is of note that a mean daily dietary vitamin D of 3 μg, combined with a median equilibrium value of 1·9 nmol/l per μg (range 0·56–2·2 nmol/l per μg(Reference Ilahi, Armas and Heaney17–Reference Cashman, Hill and Lucey25)), results in a contribution of diet to overall 25(OH)D status of about 6 nmol/l (calculated range 1·7–6·6 nmol/l), suggesting that even in the winter when levels fall to about 30–40 nmol/l, storage and release of vitamin D from tissue due to summer sun exposure is the major factor in maintaining 25(OH)D levels throughout the year.
The large study carried out by Hyppönen & Power(Reference Hyppönen and Power27) showed there was a south–north gradient in the mean plasma 25(OH)D concentrations, a finding also supported by the model using the behavioural characteristics in Table 1 and the ambient UV data in Table 2, as illustrated in Fig. 4.

Fig. 4 Regional variation in mean 25-hydroxyvitamin D (25(OH)D) levels in British people in the winter/spring (observed values(Reference Hyppönen and Power27) (![]() ) and calculated values (
) and calculated values (![]() )) and summer/autumn (observed values(Reference Hyppönen and Power27) (
)) and summer/autumn (observed values(Reference Hyppönen and Power27) (![]() ) and calculated values (
) and calculated values (![]() )). The 40th–60th percentile ranges of the observed data are represented by vertical bars.
)). The 40th–60th percentile ranges of the observed data are represented by vertical bars.
Changes in 25-hydroxyvitamin D in UV-deprived groups
The groups chosen were submariners(Reference Dlugos, Perrotta and Horn28–Reference Luria, Matsliah and Adir33) and astronauts on a long-duration mission aboard the Russian Mir space station(Reference Smith, Wastney and Morukov34). In the submariner studies, 25(OH)D was assayed immediately before the start of the patrol, just before the end of the patrol (generally 2 months) and occasionally at one or more times during the patrol. The patrols are generally deployed in the late summer when 25(OH)D levels are close to their maximum. In the case of the three astronauts, samples were taken before the start of the mission and again after 14 and 110 d. As far as can be ascertained, in none of the studies were the subjects given high doses of supplemental vitamin D nor was their diet especially enriched in vitamin D.
The data points in Fig. 5 show the relative 25(OH)D levels from each of the submariner studies (normalised to unity at the start of each patrol and assumed to be 1 August), as well as from the study in astronauts. The model was run for typical sun exposure (input values given in Table 1) up until the end of July and then UV exposure was set to zero for the remainder of the year. Using a regression technique, the fraction (f) of synthesised vitamin D stored in tissue and the half-time (γ) for tissue store clearance were determined to be 0·15 and 250 d, respectively. The relative change in plasma 25(OH)D resulting from the model calculations is shown by the solid line in Fig. 5.

Fig. 5 Modelled relative variation in 25-hydroxyvitamin D (25(OH)D) throughout the year calculated for typical outdoor behaviour up until the end of July followed by zero UV exposure for the remainder of the year (![]() ). The data points are the 25(OH)D levels relative to those at the start of the patrols in submariners and astronauts (◆, Dlugos et al. (Reference Dlugos, Perrotta and Horn28); ▲, Schlichting et al. (29); △, Preece et al. (Reference Preece, Tomlinson and Ribot30); ○, Gilman et al. (Reference Gilman, Biersner and Bondi31); ■, Holy et al. (Reference Holy, Collombet and Labarthe32); ◇, Luria et al. (Reference Luria, Matsliah and Adir33); □, Smith et al. (Reference Smith, Wastney and Morukov34)). Values are means, with standard errors represented by vertical bars. Calculated relative variation in 25(OH)D from the start of the patrols assuming f= 0 in equation 7 (
). The data points are the 25(OH)D levels relative to those at the start of the patrols in submariners and astronauts (◆, Dlugos et al. (Reference Dlugos, Perrotta and Horn28); ▲, Schlichting et al. (29); △, Preece et al. (Reference Preece, Tomlinson and Ribot30); ○, Gilman et al. (Reference Gilman, Biersner and Bondi31); ■, Holy et al. (Reference Holy, Collombet and Labarthe32); ◇, Luria et al. (Reference Luria, Matsliah and Adir33); □, Smith et al. (Reference Smith, Wastney and Morukov34)). Values are means, with standard errors represented by vertical bars. Calculated relative variation in 25(OH)D from the start of the patrols assuming f= 0 in equation 7 (![]() ), i.e. no synthesised vitamin D stored in tissue.
), i.e. no synthesised vitamin D stored in tissue.
It can be seen from the experimental data points in Fig. 5 that 25(OH)D levels in UV-deprived subjects fall to 50 % of the values at the start of the patrols at about 100–120 d; this is considerably longer than the commonly accepted plasma clearance half-life of about 25 d but is well explained by combining a 25 d half-life with a slower 250 d half-life in the two-compartment model described by equation 7. The broken line in Fig. 5 is the calculated relative variation in 25(OH)D from the start of the patrols assuming f= 0 in equation 7, i.e. no synthesised vitamin D stored in tissue.
Estimating proportion of the population who are vitamin D deficient
Studies of 25(OH)D status in British people showed a wide variation about the mean at a given period within the year(Reference Macdonald, Mavroeidi and Fraser15, Reference Rhodes, Webb and Fraser16). In keeping with the findings of others(Reference Cashman, Hill and Lucey25, Reference Hyppönen and Power27), we assume that 25(OH)D levels in a given population at a given time of year are lognormally distributed. In Table 2 of their paper, Hyppönen & Power(Reference Hyppönen and Power27) give average 25(OH)D values and the prevalence of hypovitaminosis D at three thresholds ( < 25, < 40 and < 75 nmol/l) stratified by season and demographic characteristics. From these data, we determine, using the Solver capability of Excel, that the lognormal standard deviation is 0·50, and so we can estimate the proportion of people whose 25(OH)D status falls below a given threshold. For example, if we take a mean winter level of 38 nmol/l, the percentage of subjects estimated to be vitamin D deficient (defined here as plasma 25(OH)D < 25 nmol/l(Reference Pearce and Cheetham35)) can be obtained using the Excel function LOGNORMDIST as:
The model was run with a dietary intake of 3 μg/d and the behavioural inputs given in Table 1 for women resident in southern England and northern Scotland. Fig. 6 compares the calculated and observed(Reference Macdonald, Mavroeidi and Fraser15) seasonal levels of plasma 25(OH)D, while the predicted and observed(Reference Macdonald, Mavroeidi and Fraser15) prevalence of vitamin D deficiency in each season is shown in Fig. 7. It can be seen that despite the simplistic approach to modelling human behaviour, there is a good agreement between the predicted and observed seasonal changes in 25(OH)D and the prevalence of vitamin D deficiency.

Fig. 6 Seasonal change in 25-hydroxyvitamin D (25(OH)D) in Caucasian women living in northern Scotland (observed values(Reference Macdonald, Mavroeidi and Fraser15) (![]() ) and calculated median values (
) and calculated median values (![]() )) and southern England (observed values(Reference Macdonald, Mavroeidi and Fraser15) (
)) and southern England (observed values(Reference Macdonald, Mavroeidi and Fraser15) (![]() ) and calculated median values (
) and calculated median values (![]() )). Observed values are medians with inter-quartile ranges represented by vertical bars.
)). Observed values are medians with inter-quartile ranges represented by vertical bars.

Fig. 7 Prevalence of vitamin D deficiency in Caucasian women living in northern Scotland (observed values(Reference Macdonald, Mavroeidi and Fraser15) (![]() ) and calculated values (
) and calculated values (![]() )) and southern England (observed values(Reference Macdonald, Mavroeidi and Fraser15) (
)) and southern England (observed values(Reference Macdonald, Mavroeidi and Fraser15) (![]() ) and calculated values (
) and calculated values (![]() )).
)).
Addressing vitamin D deficiency during the winter
A nationwide survey(Reference Hyppönen and Power27) in the UK showed that 16 % of the adult population have deficient levels of vitamin D ( < 25 nmol/l) during the winter and spring. We can use the model to investigate how increasing sun exposure and/or oral intake of vitamin D might lower this percentage.
There are a large number of variables that we could vary, such as the percentage of exposed BSA on weekdays and weekends for each month, or time spent outdoors during weekdays. Yet how much skin people choose to expose is constrained by ambient temperature and social norms, and the freedom to vary the time spent outdoors during weekdays is limited for most people by the demands of employment.
Consequently, we limit ourselves to two variables that people have personal control over and could choose to vary without too much external influence: the average time spent outdoors on weekend days and supplemental intakes of vitamin D during the winter months.
The model was run with the behavioural inputs given in Table 1 for a white adult population resident in the English Midlands. We assume a daily dietary intake of 3 μg with supplemental daily intake of vitamin D ranging from 0 to 30 μg during the period November through to the end of February, and with average time spent outdoors on weekend days throughout the year ranging from 1 to 4 h. These are mean times spent outdoors; in a given population there will be an appreciable variation about the mean due to propensity for being outside(Reference Diffey8). For each combination of vitamin D intake and average time spent outdoors at weekends, the mean 25(OH)D levels in the 4-month period November–February were estimated and subsequently the proportion of people who are vitamin D deficient ( < 25 nmol/l), largely as a consequence of spending less time outdoors, as:
The results are plotted in Fig. 8 where it may be seen that to achieve a vitamin D deficiency over the winter in less than 2·5 % of the population, it would require an average of 1·5 h/d spent outdoors on weekends throughout the year coupled with supplemental vitamin D intake between November and February of 28 μg/d, or alternatively 3 h/d spent outdoors on average on weekends throughout the year coupled with supplemental vitamin D intake between November and February of 11 μg/d. Keeping the average weekend outdoor exposure throughout the year to 1·5 h/d and taking a winter vitamin D supplement of 5 μg/d is estimated to result in about 10 % of the population being vitamin D deficient over the winter, a significant improvement on the estimated prevalence of 15 % deficiency if no supplement is taken and the only oral intake is 3 μg/d from the diet.

Fig. 8 Iso-prevalence plot of calculated vitamin D deficiency (25-hydroxyvitamin D (25(OH)D) < 25 nmol/l). The iso-prevalence lines represent the combinations of supplemental vitamin D during the period November through to the end of February and average hours per d spent outdoors at weekends throughout the year that would result in a given percentage of the white adult population being vitamin D deficient.
Maintaining vitamin D sufficiency throughout the year
Inspection of Fig. 3 shows that people resident in the Midlands/Wales exhibiting typical behaviour outdoors (Table 1) are estimated to have insufficient levels of plasma 25(OH)D (defined here as plasma 25(OH)D < 50 nmol/l(Reference Pearce and Cheetham35)) from November through to May. For people living in northern Scotland, this period of insufficiency is estimated to extend for 9 months from October through to June.
We use the model to examine strategies for maintaining sufficient 25(OH)D levels (i.e. >50 nmol/l) throughout the year. This can be achieved by spending more time outdoors, by supplementing dietary vitamin D intake, or a combination of both.
Relying solely on sun exposure would require spending 1·5 h/d outdoors on weekdays and 2·5 h/d outdoors at weekends throughout the year (assuming ambient UV typical of Midlands/Wales), as illustrated in Fig. 9. The problem here is that devoting this amount of time spent outdoors could prove impracticable for many people, and 2·5 h outdoor exposure on unprotected skin at weekends, especially during the summer, could lead to sunburn and compromise skin health.

Fig. 9 Modelled annual variations in 25-hydroxyvitamin D (25(OH)D) for times per d spent outdoors during weekdays and weekends of 1·5 and 2·5 h, respectively, and an oral vitamin D intake of 3 μg/d (![]() ); and times per d spent outdoors during weekdays and weekends of 1 and 1·5 h, respectively, and an oral vitamin D intake of 3 μg/d from March to October and 18 μg/d from November to February (
); and times per d spent outdoors during weekdays and weekends of 1 and 1·5 h, respectively, and an oral vitamin D intake of 3 μg/d from March to October and 18 μg/d from November to February (![]() ).
).
Alternatively, keeping outdoor exposure to typical values of 1 and 1·5 h/d on weekdays and weekends(Reference Diffey8) but increasing oral intake to 18 μg/d (3 μg/d from the diet and 15 μg/d from supplements in the 4-month period from November to February) is also predicted to maintain sufficient 25(OH)D levels throughout the year (Fig. 9). This approach is not only more likely to be adopted, but is probably safer.
Discussion
A mathematical model has been developed for estimating the variation of plasma 25(OH)D concentration throughout the year as a consequence of the oral intake of vitamin D and sun exposure of white British adults resident in different regions of the UK. Although a specific age range for using the model outputs is not given, the results may not be necessarily applicable to elderly people since the production of vitamin D in the skin decreases considerably with ageing.
The input variables related to ambient solar UV, time spent and behaviour outdoors, area of skin exposed and mean daily dietary vitamin D intake allow the examination of how these different factors affect seasonal variation. Although the results presented here are specific to the white British adult population, the model is readily adapted to other white populations by using appropriate dietary, ambient UV and behavioural data. For non-white populations, cognisance needs to be taken of the impact of constitutive pigmentation on vitamin D status(Reference Springbett, Buglass and Young36).
In the spirit of Ockham's razor, fixed values for the exposure on exposed sites relative to ambient (the exposure fraction) were used. While the values chosen for weekday and weekend exposure of 0·15 and 0·25, respectively, are representative, they are subject to variation depending on the precise activity, for example shopping or sitting at an outdoor café facing the sun(Reference Schmalwieser, Enzi and Wallisch37). From the behavioural data given in Table 1, weekday personal exposure will be about 2–3 % of ambient, with a corresponding range of 4–8 % for weekend exposure; these values are in close agreement with measured data from extensive personal UV dosimetry studies carried out in Denmark(Reference Thieden, Philipsen and Heydenreich38).
Solar UV exposure has been expressed in units of erythemal radiation (i.e. SED) and not vitamin D-effective doses, which might be thought to be more appropriate. However, given the uncertainties(Reference Norval, Björn and de Gruijl39) in the officially recognised action spectrum for the conversion of 7-dehydrocholesterol to pre-vitamin D3 in the human skin(40), which is necessary for estimating vitamin D-effective doses, coupled with the simplistic approach taken here to modelling human behaviour, it is argued that erythemal UV exposures are an adequate surrogate for vitamin D-effective exposures, especially as they are readily available from solar UV monitoring programmes (see Table 2).
Observational studies of 25(OH)D status in British people have found mean plasma 25(OH)D averaged over the year ranging from 52 to 58 nmol/l(Reference Rhodes, Webb and Fraser16, Reference Macdonald, Mavroeidi and Barr41, Reference Webb, Kift and Durkin42) with CV ranging from 37 to 48 %(Reference Rhodes, Webb and Fraser16, Reference Macdonald, Mavroeidi and Barr41). These values are close to the overall mean 25(OH)D level of 55 nmol/l and the CV of 44 % of the three modelled curves reflecting low, typical and high outdoor exposure, as shown in Fig. 3. It is well known that the time spent outdoors by a group of habitués is heterogeneous and shows a wide distribution(Reference Diffey8), and so an important contributory factor to the variance commonly observed in population studies of vitamin D status is likely to be the variation in human behaviour outdoors. There will be, of course, other factors contributing to this variance, not least genetic factors.
It is estimated that for the typical variability in the time people spend outdoors(Reference Diffey8), oral vitamin D supplementation of 28 μg/d during the period November to February is necessary to maintain 97·5 % of the population above a 25(OH)D threshold of 25 nmol/l during the winter. This dosage is appreciably higher than the mean value of 8·7 μg/d (diet plus supplements) estimated by Cashman et al. (Reference Cashman, Hill and Lucey25) to maintain late winter 25(OH)D levels greater than 25 nmol/l in 97·5 % of their population. The discrepancy is explained by the much smaller variation in 25(OH)D levels in the population studied by Cashman et al. (Reference Cashman, Hill and Lucey25) compared with the data obtained by Hyppönen & Power(Reference Hyppönen and Power27), which formed the basis of the present calculations (see equation 11).
From the data given in Table 2 of the paper by Cashman et al. (Reference Cashman, Hill and Lucey25), it can be calculated that their 25(OH)D medians and interquartile ranges lead to a lognormal standard deviation of 0·34, compared with a corresponding value of 0·50 from the observations of Hyppönen & Power(Reference Hyppönen and Power27) (see above). If the model described here is run with an oral intake of 8·7 μg/d, the late winter 25(OH)D level is estimated to be 48·4 nmol/l, and applying a lognormal standard deviation of 0·34 leads to a prevalence of deficiency ( < 25 nmol/l) of LOGNORMDIST(25, loge(48·4), 0·34) = 2·6 %, a value very close to the 2·5 % estimated by Cashman et al. (Reference Cashman, Hill and Lucey25). For the same winter 25(OH)D level of 48·4 nmol/l, the data in Table 2 of the paper by Hyppönen & Power(Reference Hyppönen and Power27) would indicate a prevalence of deficiency of LOGNORMDIST(25, loge(48·4), 0·50), which is almost 10 %.
Although the model described here provides insights into how oral vitamin D intake and behaviour outdoors have an impact upon changes in population 25(OH)D status throughout the year, it is important to recognise that there are many confounding factors that will have an influence on the use of the model at an individual level; these include the rate of vitamin D production in the skin from different parts of the body, age, obesity and degree of constitutive and facultative skin pigmentation. In principle, however, the model could be extended to account for these factors given the availability of robust experimental data that could be used to inform the additional parameters required. Such data may now be coming available(Reference McKenzie, Scragg and Liley43).
Because of its simplicity and limitations, the notion that a computational model might have credibility will not be shared by everyone, especially those who prefer to avoid mathematics(Reference Hillis44). Yet the idea that you can carry out all the trials necessary to decide between an infinite number of choices is, of course, untenable. Should we advise people to expose themselves to the sun every day, every other day or just at weekends? Or should we recognise that oral intake, either by the diet, supplements or a combination of both, is likely to be more effective and safer in reducing the proportion of the population who are vitamin D deficient? The analysis here indicates that the latter may be preferable (Fig. 9), even though the typical daily intake of vitamin D from food contributes less than sun exposure to average year-round 25(OH)D levels in both British Caucasian and Asian women(Reference Ashwell, Stone and Stolte2). It should be noted, however, that oral intake may not be free of risk, as we do not know the long-term health effects related to continued high oral intake compensating for the lack of solar UV especially during the winter.
Clinical trials, especially in the public health arena, are expensive, time consuming, often lack robustness and, unless designed appropriately, may furnish little information about how to improve upon interventions to improve public health. Mathematical models complement observational data in several ways. The measurements are precise and exactly repeatable. The costs are low and the timescales are short. In the context of oral intake of vitamin D, population exposure to solar UV radiation and the subsequent plasma levels of 25(OH)D, this is a very real advantage.
Acknowledgements
The author is grateful to Dr Tom Hill for his helpful comments on the manuscript, and to the Health Protection Agency, Chilton, for providing the ambient solar UV data. There are no conflicts of interest.













