Height-for-age, weight-for-height and weight-for-age are the three most commonly used anthropometric measures to assess the nutritional status of children. Height-for-age and weight-for-height mirror distinct biological processes( 1 ), reflecting, respectively, linear and ponderal growth. A child is stunted if its height is less than the reference corresponding to the age of the child. Similarly, a child is considered wasted if its weight-for-height is less than the reference weight-for-height. Finally, a child is under-weight if its weight is less than the reference weight for the age of the child. Weight reflects the body mass and depends on both linear and ponderal growth but fails to distinguish between the two. The proportion of children stunted, the proportion of children wasted and the proportion of children under-weight reflect the prevalence of under-nutrition in children in their own context. The three proportions are not the same and none of them reflect the multidimensional nature of child under-nutrition( Reference Svedberg 2 ). Weight-for-age has traditionally been used to estimate the prevalence of under-nutrition in children. Gomez et al. ( Reference Gomez, Galvan and Frenk 3 ) proposed a classification based on deficit in weight-for-age, which was later modified by Jelliffe( Reference Jelliffe 4 ). An Expert Committee constituted jointly by the FAO and the WHO, however, emphasised in 1971 the need for distinguishing between acute and chronic under-nutrition( 5 ), following which Waterlow & Rutishauser( Reference Waterlow and Rutishauser 6 ) proposed the stunting–wasting classification to assess child under-nutrition. Subsequently, an FAO/UNICEF/WHO Expert Committee also recommended the use of height-for-age and weight-for-height as primary indicators of the nutritional status of the child( 7 ).
India’s Integrated Child Development Scheme( 8 ), the main plank to address the challenge of child under-nutrition in the country, continues to classify a child as under-nourished on the basis of weight-for-age( 9 ). Although estimates of the prevalence of under-weight, stunting and wasting in children are also available through nationally representative household surveys such as the National Family Health Survey and the recent Rapid Survey of Children, yet, there is no system under the scheme to identify whether a child is stunted or wasted.
Recently, the rationale of using weight-for-age to measure child under-nutrition has been questioned( Reference Nandy and Miranda 10 ). It is argued that prevalence of under-weight substantially under-estimates the true prevalence of child under-nutrition( Reference Svedberg 2 , Reference Seetharaman, Chacko and Shankar 11 ). Svedberg has argued that weight-for-age is the product of height-for-age and weight-for-height and therefore assessment of child under-nutrition on the basis of child weight misses some children who are either stunted or wasted. He has proposed a composite index of anthropometric failure (CIAF) to measure the true prevalence of child under-nutrition. CIAF counts all children who are either under-weight or stunted or wasted. CIAF proposed by Svedberg is based on the classification of children into six groups: five groups comprising children with at least one anthropometric failure and the sixth group comprising children with no anthropometric failure. Nandy et al. ( Reference Nandy, Irving and Gordon 12 ) and Gaiha et al.( Reference Gaiha, Jha and Kulkarni 13 ), however, identified one more group of children who are neither stunted nor wasted but under-weight. A number of studies have, however, highlighted the limitations of CIAF( Reference Bhattacharya 14 , Reference Anwar, Gupta and Prabha 15 ), and new indices to overcome these drawbacks have been suggested( Reference Bose and Mandal 16 ).
A concern with all anthropometric indices used to assess the nutritional status of children, including CIAF, is that they are head-count ratios. They do not reflect the nutrition gap and hence tell little about the depth and severity of under-nutrition( Reference Stein 17 ). These indicators are therefore of little help in analysing nutritional inequality. There may well be a situation where nutritional inequality increases despite a decrease in the prevalence of under-nutrition or vice versa. Recently, Mukhopadhyay( Reference Mukhopadhyay 18 ) has suggested the mean of the squared deprivation gaps (MSDG) as an ideal measure of child under-nutrition and used it to measure the level, depth and severity of child under-nutrition in India( Reference Mukhopadhyay 19 , Reference Mukhopadhyay 20 ). MSDG is based on the biomedical finding that, as the nutritional shortfall increases, physiological risk increases at an increasing rate( Reference Scrimshaw, Taylor and Gordon 21 – Reference Black, Allen and Bhutta 24 ).
This paper has two objectives. The first is to decompose the difference between child weight and the weight of the reference child into the difference between child height and the height of the reference child and the difference between weight per unit height of the child and weight per unit height of the reference child. This decomposition allows to estimate the proportion of deficit in child weight attributed to the deficit in child height and deficit in weight per unit height of the child. The deficit in child weight reflects faltering in body mass growth, the deficit in child height reflects linear growth faltering, and the deficit in weight per unit height of the child reflects ponderal growth faltering. The second objective of the paper is to apply the decomposition framework to analyse the relative contribution of linear growth faltering and ponderal growth faltering to faltering of the growth of body mass in Indian children.
The paper is organised as follows. The next section develops the decomposition framework that allows decomposing the depth and severity of child under-nutrition measured in terms of body mass growth faltering into the depth and severity of child under-nutrition measured in terms of linear and ponderal growth faltering. Section three presents results of the application of the decomposition framework to Indian data. The main results and conclusions of the paper are summarised in the fourth and last section of the paper.
Decomposition of child weight
We start with the arguments put forward by Svedberg( Reference Svedberg 2 ) that neither weight-for-age nor height-for-age, nor weight-for-height, reflects the true prevalence of child under-nutrition. His arguments are based on the identity
where W is weight, H is height, and A is age. It may be noticed that the identity mentioned by Svedberg is essentially a notional identity and not a mathematical one. Weight and height are variables, whereas age is essentially a reference point so that weight per unit age and height per unit age carry little analytical meaning.
From an analytical perspective, the weight of a child of any age can be expressed as the product of its height and weight per unit height. In other words,
where U=W/H is the weight per unit height of the child. The standard approach for measuring the nutritional status of the child is to compare the weight and height of the child with the weight and height of the reference child. If W r is the weight and H r is the height for the reference child, then
Now
or
where log is the logarithm to the base 10. In other words,
where
∇W reflects the difference between the weight of the child and the weight of the reference child. Similarly, ∇H reflects the difference between the height of the child and the height of the reference child, whereas ∇U reflects the difference between the weight per unit height of the child and the weight per unit height of the reference child. Equation (2) thus shows that the difference between the weight of the child and the weight of the reference child can be decomposed into two parts, one attributed to the difference between the height of the child and the height of the reference child and the other attributed to the difference between the weight per unit height of the child and the weight per unit height of the reference child. Equation (2) thus tells how much of the difference in the growth of body mass is due to the difference in linear growth and how much of the difference is due to ponderal growth.
The difference ∇U may be further decomposed into two components. If W h denotes the reference or expected weight of the child corresponding to its actual height and U h =W h /H, then
 $$\eqalignno{ & \nabla U\,{\equals}\,{\rm log}(U/U_{r} )\,{\equals}\,{\rm log}\,((U/U_{h} ){\times}(U_{h} /U_{r} ))\,{\equals}\,{\rm log}\,(U/U_{h} ) \cr\qquad\,\,{\plus}{\rm log}\,(U_{h} /U_{r} ), \cr & \nabla U\,{\equals}\,\nabla U_{h} {\plus}\nabla U_{r} , $$
$$\eqalignno{ & \nabla U\,{\equals}\,{\rm log}(U/U_{r} )\,{\equals}\,{\rm log}\,((U/U_{h} ){\times}(U_{h} /U_{r} ))\,{\equals}\,{\rm log}\,(U/U_{h} ) \cr\qquad\,\,{\plus}{\rm log}\,(U_{h} /U_{r} ), \cr & \nabla U\,{\equals}\,\nabla U_{h} {\plus}\nabla U_{r} , $$
where
Equation (2) can now be written as
Equation (3) decomposes the difference in weight into three components: (1) difference in the height of the child from the height of the reference child, (2) difference in child weight and reference or expected weight corresponding to the child height, and (3) difference between expected or reference weight corresponding to the child height and weight corresponding to the height of the reference child. By definition, ∇U h is a measure of wasting. ∇U r , on the other hand, is the difference between the ratio of the reference weight of the child to the weight of the reference child and the height of the child to the height of the reference child. It reflects the thinness, which is a marker of poor nutritional status, although thin children may not necessarily be under-nourished.
It is obvious that ∇W, as well as ∇H, ∇U, ∇U h and ∇U r , can be both positive and negative. When ∇W<0, the child is classified as under-weight (W); when ∇H<0, the child is classified as stunted (S); and when ∇U<0, the child is classified as having low weight per unit height (U). Similarly, when ∇U h <0, the child is classified as wasted (U1). Finally, ∇U r <0 implies that the ratio of the reference weight with respect to child height is less than the ratio of the weight to height of the reference child (U2). Equation (2) suggests that when ∇H<0 and ∇U<0, ∇W is always negative or the child is always under-weight. Similarly, when ∇H≥0 and ∇U≥0, ∇W is always positive. However, when the sign of ∇H and ∇U is different, the sign of ∇W depends on the sign and magnitude of ∇H and ∇U, as shown in Table 1. The classification given in Table 1 is the same as proposed by Svedberg( Reference Svedberg 2 ).
Table 1 Classification I: nutritional status of children on the basis of Equation (2) - Svedberg classification

Source: Author.
Arguing in the same manner, Equation (3) suggests that the sign of the difference ∇W depends upon the sign and magnitude of the difference ∇H, ∇U h and ∇U r . On the basis of Equation (3), a child can be classified into one of the possible fourteen categories as shown in Table 2. It may be seen from the table that a child can be under-weight (low weight-for-age) even if it is neither stunted nor wasted as observed by Nandy et al. Reference Nandy, Irving and Gordon (12) and Gaiha et al.Reference Gaiha, Jha and Kulkarni (13) . This is the case when ∇H≥0, ∇U h ≥0 and ∇U r <0 but ∣∇U r ∣≤∣∇H+∇U h ∣. It is also obvious that when ∇U r =0, ∇U=∇U h and Equation (3) reduces to Equation (2). In other words, ∇U r reflects the stunting effect on wasting and shows that the larger the difference between H and H r , the larger the difference ∇U r . Finally, if we ignore ∇U r then the classification presented in Table 2 reduces to the classification presented in Table 3, which is the same as proposed by Nandy et al. Reference Nandy, Irving and Gordon (12) and observed by Gaiha et al.Reference Gaiha, Jha and Kulkarni (13) .
Table 2 Classification II: nutritional status of children on the basis of Equation (3)

Source: Author.
Table 3 Classification III: nutritional status of children derived from Table 2 after ignoring ∇U r

Source: Author.
Remarks: Nandy et al. ( Reference Nandy, Irving and Gordon 12 ) has also mentioned that 3.3 is not possible.
Equations (2) and (3) provide the theoretical basis in support of the classification proposed by Svedberg( Reference Svedberg 2 ) and by Nandy et al. Reference Nandy, Irving and Gordon (12) . At the same time, Equations (2) and (3) also suggest that the classification proposed by Svedberg is essentially different from the classification proposed by Nandy et al. Reference Nandy, Irving and Gordon (12) in the context of measuring ponderal growth faltering. It is therefore obvious that CIAF derived on the basis of the classification proposed by Svedberg( Reference Svedberg 2 ) (Table 1) is different from the CIAF derived from the classification proposed by Nandy et al. Reference Nandy, Irving and Gordon (12) .
The foregoing discussions suggest that a key consideration in assessing the nutritional status of children is related to the reference for measuring ponderal growth faltering. McLaren & Read( Reference McLaren and Read 25 , Reference McLaren and Read 26 ) have recommended the use of the weight per unit height of the reference child (∇U), whereas Waterlow & RutishauserReference Waterlow and Rutishauser (6) have suggested the use of the reference weight per unit height of the child (∇U h ). When ∇U is used for the purpose of classification, there is no child who is neither stunted nor having low weight per unit height but is under-weight. However, when ∇U h is used for classification, there is a proportion of children who are under-weight despite the fact that these children are neither stunted nor wasted. As ∇U=∇U h +∇U r , it is obvious that the proportion of children with ∇U<0 is always greater than or equal to the proportion of children with ∇U h <0.
Equations (2) and (3) hold for every child. Averaging ∇W, ∇H and ∇U over all children who are under-weight (∇W<0), the average deficit in weight, Avg (∇W), can be decomposed into average deficit in height, Avg (∇H), and average deficit in weight per unit height, Avg (∇U)
Similarly, the mean of the squared deficit in weight or variance of ∇W can be decomposed as
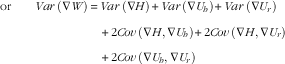 $$\eqalignno{ {\rm or}\quad \quad Var\,(\nabla W) & \,{\equals}\,Var\,(\nabla H){\plus}Var\,(\nabla U_{h} ){\plus}Var\,(\nabla U_{r} )\cr &\quad{\plus} 2Cov\,(\nabla H,\nabla U_{h} ){\plus}2Cov\,(\nabla H,\nabla U_{r} )\cr\quad{\plus}2Cov\,(\nabla U_{h} ,\nabla U_{r} ) $$
$$\eqalignno{ {\rm or}\quad \quad Var\,(\nabla W) & \,{\equals}\,Var\,(\nabla H){\plus}Var\,(\nabla U_{h} ){\plus}Var\,(\nabla U_{r} )\cr &\quad{\plus} 2Cov\,(\nabla H,\nabla U_{h} ){\plus}2Cov\,(\nabla H,\nabla U_{r} )\cr\quad{\plus}2Cov\,(\nabla U_{h} ,\nabla U_{r} ) $$
Here Cov stands for covariance. Equation (6) can also be written as
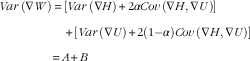 $$\eqalignno{ Var\,(\nabla W) & \,{\equals}\,\left[Var\,(\nabla H){\plus}2\alpha Cov\,(\nabla H,\nabla U)\right] \cr\quad{\plus} \left[Var\,(\nabla U){\plus}2\left( {1{\minus}\alpha } \right)Cov\,(\nabla H,\nabla U)\right] \cr{\equals}\,A{\plus}B $$
$$\eqalignno{ Var\,(\nabla W) & \,{\equals}\,\left[Var\,(\nabla H){\plus}2\alpha Cov\,(\nabla H,\nabla U)\right] \cr\quad{\plus} \left[Var\,(\nabla U){\plus}2\left( {1{\minus}\alpha } \right)Cov\,(\nabla H,\nabla U)\right] \cr{\equals}\,A{\plus}B $$
where α is the proportion of Cov (∇H, ∇U) attributed to ∇H. Similarly,
 $$\eqalignno{ Var\,(\nabla W) \,{\equals}\,[Var\,(\nabla H){\plus}2\alpha Cov\,(\nabla H,\nabla U_{h} )\cr{\plus}2\left( {1{\minus}\gamma } \right) Cov\((\nabla U_{r} ,\nabla H)] {\plus}[Var\,(\nabla U_{h} )\cr{\plus}2\left( {1{\minus}\alpha } \right)Cov\,(\nabla H,\nabla U_{h} )\cr{\plus}2\beta Cov\,(\nabla U_{h} ,\nabla U_{r} )]{\plus} [Var\,(\nabla U_{r} ) \cr{\plus}2{\rm }\gamma Cov\,(\nabla H,\nabla U_{r} ){\plus}2\left( {1{\minus}\beta } \right)Cov\,(\nabla U_{h} ,\nabla U_{r} )] \cr\!\!\!\!\!{\equals}\,C{\plus}D{\plus}E $$
$$\eqalignno{ Var\,(\nabla W) \,{\equals}\,[Var\,(\nabla H){\plus}2\alpha Cov\,(\nabla H,\nabla U_{h} )\cr{\plus}2\left( {1{\minus}\gamma } \right) Cov\((\nabla U_{r} ,\nabla H)] {\plus}[Var\,(\nabla U_{h} )\cr{\plus}2\left( {1{\minus}\alpha } \right)Cov\,(\nabla H,\nabla U_{h} )\cr{\plus}2\beta Cov\,(\nabla U_{h} ,\nabla U_{r} )]{\plus} [Var\,(\nabla U_{r} ) \cr{\plus}2{\rm }\gamma Cov\,(\nabla H,\nabla U_{r} ){\plus}2\left( {1{\minus}\beta } \right)Cov\,(\nabla U_{h} ,\nabla U_{r} )] \cr\!\!\!\!\!{\equals}\,C{\plus}D{\plus}E $$
where β is the proportion of Cov (∇U h , ∇U r ) attributed to ∇U h and γ is the proportion of Cov (∇U r , ∇H) attributed to ∇U r .
Equation (4) shows that the average deficit in W can be decomposed into average deficit in H and average deficit in U or equivalently average deficit in U h and average deficit in U r (Equation 5). Similarly, Equation (8) shows that the average squared deficit in W can be decomposed into the average squared deficit in H and average squared deficit in U, whereas Equation (9) shows that the average squared deficit in W can be decomposed into average squared deficit in H, average squared deficit in U h and average squared deficit in U r . In other words, Equations (4) and (5) analyse how linear growth faltering and ponderal growth faltering contribute to the faltering in the growth of body mass of the child. Similarly, Equations (8) and (9) analyse how the severity of faltering in linear growth and the severity of faltering in ponderal growth contribute to the severity of faltering in the growth of the body mass of the child.
Application of Equations (8) and (9) requires estimation of α, β and γ. It may be noticed that Cov (x,y) depends upon the variation in x and variation in y. If x and y are independent then Cov (x,y) is zero and
In the present case, ∇H, ∇U h and ∇U r are, by definition, not independent. As such, we have applied the principal component analysis to identify the linear combination of the variables that account for the largest proportion of the total variation across the variables to obtain estimates of α, β and γ. To estimate α, we have applied the principal component analysis using ∇H and ∇U h , and the normalised squared loading of ∇H in the first principal component has been taken as the value of α. Similarly, principal component analysis using ∇U h and ∇U r has been carried out and the normalised squared loading of ∇U h in the first principal component has been taken as the value of β. Finally, principal component analysis using ∇U r and ∇H has been carried out and the normalised squared loading of ∇U r in the first principal component has been taken as the value of γ. The application of principal component analysis revealed that in all the three cases the first principal component accounted for at least 80 % of the total variation in the data set, which justifies taking normalised squared loadings as weights in Equations (8) and (9).
Evidence from India
We apply the analytical framework developed above to revisit the nutritional status of children below 3 years of age in India using data from National Family Health Survey 1992–93, 1998–99 and 2005–06( 27 – 29 ). During these surveys, the weight and height of all children below 3 years of age in the sampled households were measured following standard anthropometric measurement methods. On the basis of these measurements, z-scores were calculated using World Health Organization Standards (30) . At the first step of the analysis, children having very high (z>6) and very low (z<−6) z-scores were excluded so that the analysis was limited to 20 831 children below 3 years of age surveyed during 1992–93, to 25 490 children surveyed during 1998–99 and to 24 904 children surveyed during 2005–06. More recent data on the weight and height of children below 3 years of age in India are available through the District Level Household and Facility Survey 2012–13 (31) and the Rapid Survey of Children 2013–14 (32) . District Level Household and Facility Survey 2012–13 was confined to only twenty-one states and Union Territories of the country. It did not cover states that are termed as the Empowered Action Group states, which include Bihar, Chhattisgarh, Jharkhand, Madhya Pradesh, Odisha, Rajasthan, Uttar Pradesh, Uttarakhand and Odisha. This survey did not cover Delhi, Gujarat, Jammu and Kashmir and Union Territories Dadra and Nagar Haveli, Daman and Diu and Lakshadweep. The Rapid Survey of Children 2013–14 (32) did not cover the Union Territories of the country. Moreover, unit-level data from this survey are yet to be released. As such, the data from these two most recent surveys have not been used in the present analysis.
Prevalence of under-nutrition
Estimates of the prevalence of under-nutrition in children below 3 years of age in India according to classifications described in Tables 1–3 are presented in Tables 4–6. The prevalence of under-weight and the prevalence of stunting are the same in the three classifications but the prevalence of weight per unit height as obtained in classification I is different from the prevalence of wasting in classification III because weight per unit height is measured relative to the weight per unit height of the reference child in classification I, whereas wasting is measured relative to the reference weight per unit height of the child in classification III. The proportion of children who are under-weight as well as stunted and having low weight for height is therefore higher on the basis of classification I than on the basis of classification III. Similarly, CIAF and the proportion of children with low weight for height are higher in classification I, compared with classification III.
Table 4 Prevalence of under-nutrition in India, 1992–2006 based on classification I

Source: Author’s calculations.
Classification II brings in the element of thinness in the assessment of nutritional status (Table 5). More than 80 % of children in India are thin and almost 40 % of them are neither stunted nor wasted nor under-weight. Although there is no growth faltering in nearly half of these thin children, the expected growth of body mass relative to their height in these children is less than the weight of the reference child relative to its height. The proportion of children who are thin but not under-nourished is substantially higher than the proportion of children who are wasted. Thinness of ‘normal’ children indicates that there exists substantial nutritional deficiency even in those children who are otherwise classified as ‘normal’. This nutritional deficiency in ‘normal’ children is not reflected in either classification I or classification III. If thinness is not taken into consideration, then the CIAF based on classification II (Table 5) is the same as the CIAF based on classification III (Table 6). If thinness is also taken into account, then Table 5 suggests that almost 90 % of the Indian children suffer from some type of nutritional deficiency and there appears little change in this proportion over time. It also appears that the proportion of children who are thin but not under-nourished has increased over time.
Table 5 Prevalence of under-nutrition in India, 1992–2006, based on classification II

Source: Author’s calculations.
Table 6 Prevalence of under-nutrition in India, 1992–2006, based on classification III
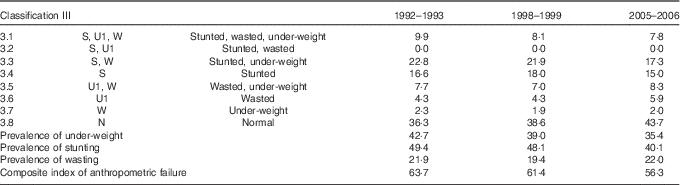
Source: Author’s calculations.
The difference in the nutritional status of children based on classification I and classification III becomes sharper when stunting and wasting are considered simultaneously. Classification III lowers the proportion of children with both linear and ponderal growth faltering but increases the proportion of children with linear growth faltering. According to classification I (Table 4), there is no child who is neither stunted nor has low weight-for-height but is under-weight, whereas according to classification III (Table 6) there are >4 % such children in 2005–2006. It is also clear that the two classifications will give the same assessment only when ∇U r =0, which means that a child taller than the reference child must also be heavier than the reference child and a child shorter than the reference child must also be lighter than the reference child( Reference Cole 33 , Reference Cole 34 ).
Depth of under-nutrition
Table 7 presents the average values of ∇W, ∇H, ∇U, ∇U h and ∇U r for under-weight (∇W<0) children. The table shows that faltering in the growth of body mass is primarily due to faltering in ponderal growth, on average. When ∇U is decomposed into ∇U h and ∇U r , then only about 5 % of Avg (∇W) is accounted for by Avg (∇U h ), whereas >72 % of Avg (∇W) is accounted for by Avg (∇U r ). Moreover, the contribution of linear growth faltering to faltering in the growth of body mass has decreased over time but that of ponderal growth has increased. When ponderal growth faltering is decomposed further, the dominance of the weight component of ponderal growth faltering may be seen becoming more dominant than the height component. This observation confirms that faltering in the growth of body mass in Indian children is primarily due to faltering in ponderal growth.
Table 7 Average deficit in the weight of children below 3 years of age and its components in India
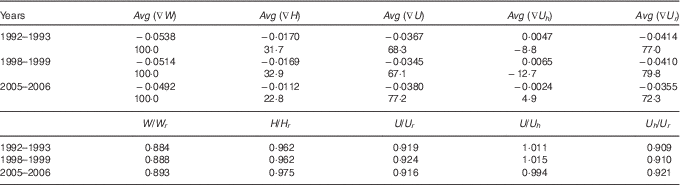
Source: Author’s calculations.
Table 7 also reveals that the weight deficit of Indian children has, on average, decreased over time, albeit slowly. Among children deficient in weight, the average deficit in height remained unchanged between 1992–1993 and 1998–1999 but decreased sharply between 1998–1999 and 2005–2006, whereas the average deficit in weight per unit height decreased between 1992–1993 and 1998–1999 but increased between 1998–1999 and 2005–2006. On the other hand, the ratio (U/U h ) was >1 in 1992–1993 and 1998–1999 but decreased to <1 in 2005–2006, but the ratio (U h /U r ) increased throughout the period under reference. If there had been no decrease in the ratio (U/U h ), then the reduction in weight deficit would have been even faster.
Severity of under-nutrition
The mean squared deficit in weight, Var (∇W), reflects the severity of under-nutrition in terms of body mass growth faltering. Table 8 shows that the severity of body mass growth has decreased over time, although the decrease has been slow. The primary contributor to the severity of body mass growth faltering has been the severity in ponderal growth faltering. However, the contribution of the severity of ponderal growth faltering has decreased over time but that of linear growth faltering has increased. The decrease in the contribution of the severity of ponderal growth faltering has been the result of the decrease in the contribution of the severity in the deficit measured in terms of ∇U h , despite the fact that the contribution of the severity of the deficit measured in terms of ∇U r has increased. In 2005–2006, the severity of ∇H, ∇U h and ∇U r contributed almost equally to the severity of ∇W. This was not the case in 1992–1993 when the severity of ∇U h was the primary contributor to the severity in body mass growth faltering.
Table 8 Severity of deficit in weight (mean of the squared deficit in weight) and its components in India
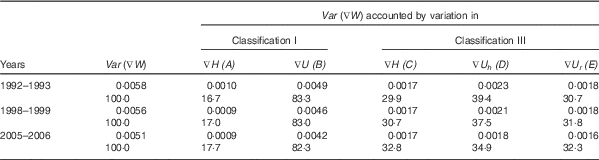
Source: Author’s calculations.
Estimates of CIAF based on classification III obtained in the present analysis are almost the same as the estimates obtained by Nandy et al. Reference Nandy, Irving and Gordon (12) and Gaiha et al.Reference Gaiha, Jha and Kulkarni (13) . On the basis of the data available through the National Family Health Survey of 1998–99, Nandy et al. Reference Nandy, Irving and Gordon (12) estimated that 59·8 % of children below 3 years of age in India were under-nourished in at least one dimension of child under-nutrition. On the other hand, Gaiha et al.Reference Gaiha, Jha and Kulkarni (13) , using the data available from the Indian Human Development Survey of 2005 (35) , estimated that approximately 58·6 % of children below 5 years of age were under-nourished in at least one dimension of anthropometric failure. By comparison, the present analysis estimates a CIAF of approximately 61 % for India on the basis of the National Family Health Survey of 1998–99 and a CIAF of approximately 56 % on the basis of the National Family Health Survey of 2005–06. The prevalence of under-weight, stunting and wasting obtained in the present analysis has, however, been found to be different from those obtained by Nandy et al. Reference Nandy, Irving and Gordon (12) and Gaiha et al.Reference Gaiha, Jha and Kulkarni (13) . The prevalence of under-weight estimated by Nandy et al. Reference Nandy, Irving and Gordon (12) and Gaiha et al.Reference Gaiha, Jha and Kulkarni (13) is, however, higher than the prevalence of either stunting or wasting. As argued by Svedberg( Reference Svedberg 2 ) and as shown in the present paper, deficit in child weight is essentially a multiple of the deficit in child height and the deficit in per unit height of the child. As such, the proportion of children who are deficit in terms of weight should be between the proportion of children deficit in terms of height (stunted) and the proportion of children deficit in terms of weight per unit height.
Discussions and conclusions
We have shown in this paper that the level, depth and severity of body mass growth faltering can be decomposed into the level, depth and severity of linear growth faltering and the level, depth and severity of ponderal growth faltering. This decomposition provides theoretical justification of the classification of the nutritional status of children proposed by Svedberg( Reference Svedberg 2 ) and Nandy et al. Reference Nandy, Irving and Gordon (12) . The essential difference between the Svedberg classification and the classification proposed by Nandy et al. is the way ponderal growth faltering is measured. When ponderal growth faltering is measured relative to the weight and height of the reference child, the decomposition analysis leads to Svedberg’s( Reference Svedberg 2 ) classification. When ponderal growth faltering is measured relative to the reference weight for the height of the child, the decomposition analysis leads to the classification suggested by Nandy et al. ( Reference Nandy, Irving and Gordon 12 ). Measuring ponderal growth faltering relative to the reference weight for the height of the child, however, leads to an under-estimation of the prevalence of under-nutrition as measured in terms of CIAF and lowers the prevalence of ponderal growth faltering. Another anomaly associated with the use of reference weight for the height of the child for measuring ponderal growth faltering is that some children are classified as under-weight despite the fact that they are neither stunted nor wasted. These measurement problems can be effectively addressed when ponderal growth faltering is measured relative to the weight and height of the reference child. The decomposition framework also suggests that when ponderal growth faltering is measured relative to the weight and height of the reference child, faltering in body mass growth is fully explained by ponderal growth faltering and linear growth faltering.
The application of the decomposition framework to the Indian data indicates that different classifications depict different situations of child under-nutrition, especially in the context of ponderal growth faltering. When ponderal growth is measured relative to the weight and height of the reference child, the primary determinant of the level, depth and severity of body mass growth faltering is the faltering in ponderal growth. Moreover, a substantial proportion of Indian children are thin in the sense that their weight per unit height, on average, is less than the weight per unit height of the reference child. These children are not under-nourished as they are neither under-weight nor stunted nor wasted and so they remain out of the gambit of efforts directed towards tackling the problem of child under-nutrition in India. Addressing the nutritional deficiency of these ‘normal’ children is one of those dimensions of child under-nutrition that remains uncovered under the existing nutrition efforts in the country.
The decomposition analysis carried out in this paper leads to at least three constructs of CIAF, which give three different prevalence rates of child under-nutrition in India. CIAF based on classification III is the lowest among the three, whereas classification II suggests that body mass growth faltering is nearly universal in children below 3 years of age in India. The primary purpose of developing CIAF has been to relate various combinations of anthropometric failure to adverse outcomes. On the basis of classification III, Nandy et al. ( Reference Nandy, Irving and Gordon 12 ) have shown that children who are, at the same time, stunted, wasted and under-weight have relatively the highest risk of having diarrhoea and acute respiratory infections. Nandy et al. ( Reference Nandy, Irving and Gordon 12 ) have also shown that CIAF is the highest in households with the highest level of poverty. Similar observations have been made by Gaiha et al.( Reference Gaiha, Jha and Kulkarni 13 ). It would be interesting to carry out a similar analysis using classification III. This is, however, not within the scope of the present paper.
Acknowledgements
The author is grateful for the comments of the learned referees who contributed towards improving the paper.
There is no funding support for this study.
There is no conflict associated with this study.











