On peut penser que la dimension des sinistres est la résultante d'un très grand nombre de causes indépendantes à effets positifs.
Soient
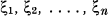
les variables aléatoires indépendantes qui représentent les facteurs élémentaires exerçant leur action dans l'ordre indiqué par les indices.
Si Xν est l'ampleur du sinistre dû aux facteurs ξ1, ξ2, …., ξν nous pouvons supposer que l'augmentation causée par ξν+1 soit proportionelle à ξν+1 et à une certaine fonction, g(Xν) de la dimension Xν.
C'est à dire, nous supposons qu'il y ait les relations:

Si chaque facteur n'apporte qu'un faible contribut à l'augmentation du sinistre, nous pouvons alors poser approximativement aussi:
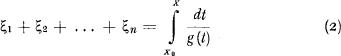
Comme X varie de Xo à Xn (et que X = Xn désigne la dimension extrème du sinistre) le second membre de la (2) décrit une variable aléatoire, fonction de X.
Puisque par hypothèse ξ1,, ξ2, …., ξn sont des variables aléatoires indépendante, si n est suffisament grand, d'après le théorème de la limite des probabilités il s'insuit que la variable aléatoire au second membre de la (2), est, à la limite, distribuée suivant la loi normale. Si l'on pose g(t) = t − c, la variable aléatoire normale qui décrit la dimension du sinistre pourra être posée dans la forme In(X − c).