Article contents
The unearned no claim bonus
Published online by Cambridge University Press: 29 August 2014
Extract
1. The claims experience of a motorcar insurance is assumed to give some indication about the risk (basic claim frequency) of that insurance. The experience rating systems in motor insurance are based on this supposition. In these systems the premium to be paid in some year is a function of the individual claims experience of preceding years. That premium can be considered as the difference between:
— a basic premium, being the expected value of the premium to be paid for insurances with a basic claim frequency equal to the mean value of the basic claim frequency of the portfolio or the tariff class.
— a positive or negative bonus; although in the negative case the word bonus is misleading this word will nevertheless be used for both cases in this paper.
The bonus usually consists of at least the following components:
a. a component concerning the individual claim frequency.
b. an individual random factor.
c. a collective random factor.
Other factors, like the effect of the trend in the claim frequencies and the effect of the dependence of the claim frequency of age and experience of the driver are not taken into account in this paper.
2. The meaning of the three components mentioned in section I can be demonstrated by the following example.
The structure function U(χ) of the portfolio, being the distribution function of the individual basic claim frequencies χ is assumed to be defined by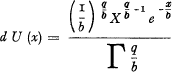 representing a gamma distribution with expected value q and variance qb. The probability Pi for an insurance to have i claims in a certain year is supposed to be
representing a gamma distribution with expected value q and variance qb. The probability Pi for an insurance to have i claims in a certain year is supposed to be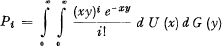
In this formula the factor y has the same value for all insurances in the portfolio in a certain year but varies from year to year according to the distribution function G(y) with expected value 1 and variance 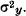 .
.
Information
- Type
- Astin Colloquium 1966 Arnhem Subject one
- Information
- Copyright
- Copyright © International Actuarial Association 1968
- 3
- Cited by

