Article contents
On the Use of Extreme Values to Estimate the Premium for an Excess of Loss Reinsurance
Published online by Cambridge University Press: 29 August 2014
Extract
I. Suppose that the claims experienced by a portfolio could be represented as independent random variables with a distribution function F(x). The net premium per claim for an excess loss cover above an amount of L is then
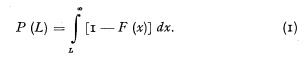
If we have no information about F(x) except a number M of independent claims, we might compute the observed “staircase” distribution function SM (x) which is for every x an unbiased estimate of F(x), and could thus compute an unbiased estimate for P(L) with the variance [7])
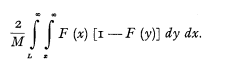
2. In real life we have some qualitative knowledge of F(x) and very limited information about the claims. In his introduction to this subject Beard treats the case where the only information about F(x) consists of the largest claim xi and the number of claims ni (i = 1, 2, …, N) observed during N periods (Reference No 2). It is known from the theory of extreme values [3] that for large ni the distribution of xi depends mainly on the parameters uni and αni( defined by
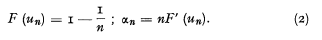
Beard further assumes that F(x) belongs to what is called by Gumbel “the exponential type” of distribution functions, which have an unlimited tail and finite moments. This class is strictly defined by Gnedenko's necessary and sufficient condition [4, p. 68]:
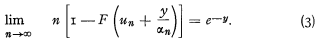
Information
- Type
- Papers
- Information
- Copyright
- Copyright © International Actuarial Association 1964
References
REFERENCES
- 10
- Cited by

