Article contents
On The Approximation of the Total Amount of Claims
Published online by Cambridge University Press: 29 August 2014
Extract
Several “short cut” methods exist to approximate the total amount of claims ( = χ) of an insurance collective. The classical one is the normal approximation
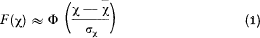
where 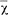 and σx are the mean value and standard deviation of x. Φ is the normal distribution function.
and σx are the mean value and standard deviation of x. Φ is the normal distribution function.
It is well-known that the normal approximation gives acceptable accuracy only when the volume of risk business is fairly large and the distribution of the amounts of the individual claims is not “too dangerous”, i.e. not too heterogeneous (cf. fig. 2).
One way to improve the normal approximation is the so called NP-method, which provides for the standardized variable 
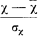 a correction Δz
a correction Δz
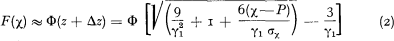
where

is the skewness of the distribution F(χ). Another variant (NP3) of the NP-method also makes use of the moment μ4, but, in the following, we limit our discussion mainly to the variant (2) (= NP2).
If Δz is small, a simpler formula
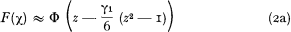
is available (cf. fig. 2).
Another approximation was introduced by Bohman and Esscher (1963). It is based on the incomplete gamma function
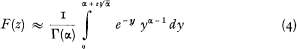
where 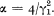
Experiments have been made with both formulae (2) and (4); they have been applied to various F functions, from which the exact (or at least controlled) values are otherwise known. It has been proved that the accuracy is satisfactory provided that the distribution F is not very “dangerous”.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © International Actuarial Association 1977
References
- 9
- Cited by

